42 Transformações lineares

A definição de transformações lineares

Sejam $V,W$ dois espaços vetoriais. Já que $V,W$ são conjuntos, faz sentido considerar uma função $f:V\to W$ (logo $f$ leva cada vetor de $V$ em um vetor de $W$). Mas uma função qualquer vai geralmente fazer uma bagunça total. As funções melhores $V\to W$ são aquelas que “respeitam as estruturas de $V$ e $W$ como espaços vetoriais”. Tais funções são as seguintes:

Definição 42.1 Sejam $V,W$ dois espaços vetoriais sobre $\R$. Uma função $T:V\to W$ é uma transformação linear (TL) se

$T(\ul{u} + \ul{v}) = T(\ul{u}) + T(\ul{v})\quad\forall \ul{u}, \ul{v}\in V$,
$T(\lambda \ul{v}) = \lambda T(\ul{v})\quad\forall \lambda\in \R,\,\forall \ul{v}\in V$.

Exemplo 42.1

Sejam $V,W$ espaços vetoriais e $Z:V\to W$ a transformação nula, que leva cada $\ul{v}\in V$ no vetor $\ul{0}$. Vamos confirmar que $Z$ é uma transformação linear: \[Z(\ul{u} + \ul{v}) = \ul{0} = \ul{0} + \ul{0} = Z(\ul{u}) + Z(\ul{v})\quad\forall \ul{u}, \ul{v}\in V\quad\checkmark\] \[Z(\lambda\ul{v}) = \ul{0} = \lambda\cdot \ul{0} = \lambda Z(\ul{v})\quad\forall\lambda\in \R, \forall \ul{v}\in V\quad\checkmark\]
A função identidade $I:V\to V$ é uma transformação linear: \[I(\ul{u} + \ul{v}) = \ul{u} + \ul{v} = I(\ul{u}) + I(\ul{v})\quad\forall \ul{u}, \ul{v}\in V\quad\checkmark\] \[I(\lambda\ul{v}) = \lambda\ul{v} = \lambda I(\ul{v})\quad\forall\lambda\in \R, \ul{v}\in V\quad\checkmark\]
A função $T: \R^2\to \R$ definida como $T(x,y) = 2x-y$ é uma TL: \[\begin{aligned} T\left((x,y) + (x',y')\right) & = T\left((x+x',y+y')\right) \\ & = 2(x+x')-(y+y)' \\ & = 2x-y+2x'-y' \\ & = T\left((x,y)\right) + T\left((x',y')\right)\quad\checkmark \end{aligned}\] \[\begin{aligned} T(\lambda(x,y)) & = T\left((\lambda x, \lambda y)\right) \\ & = 2\lambda x - \lambda y \\ & = \lambda(2x-y) \\ & = \lambda T\left((x,y)\right).\quad\checkmark \end{aligned}\]
A função $T:\R[x]\to \R[x]$ que manda $f(x)\in\R[x]$ para $xf(x)$ é uma transformação linear – exercício.
A função $T : \R \to \R$ que manda $x$ para $x+1$ não é uma transformação linear: \[T(1+1) = T(2) = 2+1 = 3\] \[T(1)+T(1) = (1+1) + (1+1) = 4 \neq 3.\]
(Super importante!) Seja $A$ uma matriz $n\times m$. Dado um vetor $\ul{v}$ de $\R^m$, tratado com vetor coluna $m\times 1$, o produto \[A\ul{v}\] é um vetor coluna $n\times 1$, logo $A\ul{v}$ é um vetor de $\R^n$. Assim, obtemos uma função \[\begin{aligned} T_A\,:\, \R^m & \to \,\R^n \\ \ul{v}\,\,\, & \mapsto A\ul{v}. \end{aligned}\] Afirmo que $T_A$ é uma TL. Já que estamos somente multiplicando matrizes, temos \[T_A(\ul{u} + \ul{v}) = A(\ul{u} + \ul{v}) = A\ul{u} + A\ul{v} = T_A(\ul{u}) + T_A(\ul{v})\quad\forall \ul{u},\ul{v}\in \R^m,\] \[T_A(\lambda\ul{v}) = A\cdot\lambda\ul{v} = \lambda A\ul{v} = \lambda T_A(\ul{v})\quad\forall\lambda\in \R, \forall \ul{v}\in \R^m.\] Vamos fazer uns exemplos disso:
- Seja $A = \begin{pmatrix} 1 & 0 & -3 \\ 2 & 1 & 5 \end{pmatrix}$. Então $T_A: \R^3\to \R^2$ é a transformação linear dada por \[T_A\begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 1 & 0 & -3 \\ 2 & 1 & 5 \end{pmatrix}\cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x - 3z \\ 2x + y + 5z \end{pmatrix}\in \R^2.\]
- Exemplos 1-3 acima podem ser interpretados dessa forma:
  - A transformação nula $\R^m\to \R^n$ é a transformação $T_{\ul{0}}$ correspondente à matriz nula $n\times m$ \[\ul{0} = \begin{pmatrix} 0 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & 0 \end{pmatrix},\] pois $T_{\ul{0}}(\ul{v}) = \ul{0}\cdot\ul{v} = \ul{0}\,,\forall \ul{v}\in \R^m$.
  - A transformação identidade $\R^n\to \R^n$ é $T_I$, onde $I$ é a matriz identidade $n\times n$ \[I = \begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & & 0 \\ \vdots & & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix},\] pois $T_{I}(\ul{v}) = I\ul{v} = \ul{v}\,\,\forall \ul{v}\in \R^n$.
  - A transformação $T:\R^2\to \R$ de Exemplo 3 corresponde a $T_A$, em que $A$ é a matriz $1\times 2$ \[A = \begin{pmatrix} 2 & -1 \end{pmatrix},\] pois \[T_A\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 2 & -1 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 2x - y \end{pmatrix} = T((x,y)).\]
- A transformação linear correspondente à matriz quadrada \[A = \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}\] é a “projeção no eixo $x$”: \[T_A\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x \\ 0 \end{pmatrix}:\]
  
  Similarmente, a matriz $n\times n$ $E_{ii}$ corresponde à transformaçaõ linear $\R^n\to \R^n$ “projeção na coordenada $i$”: \[T_{E_{ii}}\begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_i \\ \vdots \\ x_n \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ \vdots \\ x_i \\ \vdots \\ 0 \end{pmatrix}.\]

Exercício 42.1 Seja $T\colon V\to W$ uma transformação linear, sejam $\ul{v_1},\ldots,\ul{v_k}\in V$ e $\lambda_1,\ldots,\lambda_k\in\R$. Mostre que \[T(\lambda_1\ul{v_1}+\cdots+\lambda_k\ul{v_k})=\lambda_1T(\ul{v_1})+\cdots+\lambda_kT(\ul{v_k}).\] Este exercício diz que uma transformação linear leva uma combinação linear de vetorores para a combinação linear das suas imagens com os mesmos coeficientes.

Proposição 42.1 Qualquer transformação linear $T : V\to W$ leva $\ul{0}$ em $\ul{0}$.

Comprovação. O vetor $\ul{0} = 0\cdot \ul{0}$. Logo \[T(\ul{0}) = T(0\cdot\ul{0}) = 0\cdot T(\ul{0}) = \ul{0}.\] ◻

Sejam $V,W$ espaços vetoriais. Podemos considerar o conjunto de todas as transformações lineares de $V$ a $W$: \[\mathcal{L}(V,W) := \{T: V\to W\,|\,T\hbox{ uma transformação linear}\}.\]

Teorema 42.1 $\mathcal{L}(V,W)$ é um espaço vetorial.

Comprovação. Já que elementos de $\mathcal{L}(V,W)$ são funções $V\to W$, \[\mathcal{L}(V,W)\subseteq \mathcal{F}(V,W).\] Então só precisamos confirmar que $\mathcal{L}(V,W)$ é subespaço de $\mathcal{F}(V,W)$. Ou seja, que a soma de duas TLs é uma TL, e que o produto por escalar de uma TL é uma TL. Então sejam $S,T\in \mathcal{L}(V,W)$ e $\ul{u}, \ul{v}\in V, \lambda\in \R$. \[\begin{aligned} (S+T)(\ul{u}+\ul{v}) & = S(\ul{u}+\ul{v}) + T(\ul{u}+\ul{v})\qquad\qquad(\hbox{def de soma em }\mathcal{F}(V,W)) \\ & = S(\ul{u}) + S(\ul{v}) + T(\ul{u}) + T(\ul{v}) \quad (S,T\hbox{ são TLs}) \\ & = S(\ul{u}) + T(\ul{u}) + S(\ul{v}) + T(\ul{v}) \\ & = (S+T)(\ul{u}) + (S+T)(\ul{v})\qquad\qquad\checkmark \end{aligned}\] Similarmente \[\begin{aligned} (S+T)(\lambda\ul{u})& = S(\lambda\ul{u}) + T(\lambda\ul{u}) \\ & = \lambda S(\ul{u}) + \lambda T(\ul{u}) \\ & = \lambda (S(\ul{u}) + T(\ul{u})) \\ & = \lambda (S+T)(\ul{u}).\qquad\qquad\checkmark \end{aligned}\] Logo $S+T$ é transformação linear.

Exercício: Sejam $T\in \mathcal{L}(V,W)$ e $\lambda\in \R$. Mostre que a função $\lambda T$ é uma transformação linear.

Então $\mathcal{L}(V,W)$ é fechado por somas e produtos por escalar. Ou seja, $\mathcal{L}(V,W)$ é subespaço de $\mathcal{F}(V,W)$. ◻

Exemplo 42.2 No caso especial em que $W = \R$, o espaço vetorial $\mathcal{L}(V,\R)$ se chama o espaço dual de $V$ e está denotado por $V^*$. Os elementos de $V^*$ são transformações lineares $V\to \R$ e são chamados de funcionais ou formas lineares de $V$.

Transformações lineares e matrizes

Quando temos dois conjuntos $B,C$, é muito fácil definir uma função $f:B\to C$, pois pode mandar os elementos de $B$ para $C$ como quiser, sem condições nenhumas. Com uma transformação linear $T:V\to W$, não temos tanta liberdade: temos que mandar $\ul{0}$ para $\ul{0}$, por exemplo, e $T$ tem que preservar soma e múltiplo escalar. Mas vamos ver que, de fato, transformações lineares são “igualmente fáceis” como funções, de alguma forma.

Teorema 42.2 Sejam $V$ um espaço vetorial com base $B$ e $W$ outro espaço vetorial. Seja $f:B\to W$ uma função qualquer. Então existe uma única transformação linear $T_f:V\to W$ com a propriedade que \[T_f(\ul{b}) = f(\ul{b})\quad\hbox{para todo }\ul{b}\in B.\]

Este teorema diz que “transformações lineares de $V$ a $W$ são a”mesma coisa” como funções de uma base de $V$ a $W$“. Vamos prová-lo:

Comprovação. Dada uma função $f:B\to W$, como vamos definir a transformação linear $T_f$? Já que $B$ é uma base, todo vetor $\ul{v}\in V$ pode ser escrito como uma combinação linear \[\ul{v} = \lambda_1\ul{b_1} + \cdots + \lambda_n\ul{b_n}\] de elementos de $B$. Já que $T_f$ é TL e $T_f(\ul{b}) = f(\ul{b})\,\forall b\in B$, estamos obrigados a definir \[\begin{aligned} T_f(\ul{v}) & = T_f(\lambda_1\ul{b_1} + \cdots + \lambda_n\ul{b_n}) \\ & = \lambda_1T_f(\ul{b_1}) + \cdots + \lambda_nT_f(\ul{b_n}) \quad(T_f\hbox{ TL})\\ & = \lambda_1f(\ul{b_1}) + \cdots + \lambda_nf(\ul{b_n})\quad\,\,(T_f(\ul{b_i}) = f(\ul{b_i})). \end{aligned}\] Temos que confirmar umas coisas, todas sendo fáceis:

$T_f$ é bem definida. Isto é, que não mandamos o mesmo elemento de $V$ para dois lugares diferentes sem querer. Mas isso segue pois todo elemento de $V$ tem uma única expressão como combinação linear dos elementos da base.
$T_f$ é TL. Dados $\ul{u}, \ul{v}\in V$, escreva \[\ul{u} = \lambda_1 \ul{b_1} + \cdots + \lambda_n\ul{b_n}\] \[\ul{v} = \mu_1 \ul{b_1} + \cdots + \mu_n\ul{b_n},\] (já que alguns dos $\lambda_i, \mu_i$ podem ser $0$, não tem problema de escrever assim). Então, \[\begin{aligned} T_f(\ul{u} + \ul{v}) & = T_f\left((\lambda_1 + \mu_1) \ul{b_1} + \cdots + (\lambda_n + \mu_n)\ul{b_n}\right) \\ & = (\lambda_1 + \mu_1) f(\ul{b_1}) + \cdots + (\lambda_n + \mu_n)f(\ul{b_n}) \\ & = \left(\lambda_1f(\ul{b_1}) + \cdots + \lambda_nf(\ul{b_n})\right) + \left(\mu_1 f(\ul{b_1}) + \cdots + \mu_nf(\ul{b_n})\right) \\ & = T_f(\ul{u}) + T_f(\ul{v}). \end{aligned}\] Exercício: Prove que $T_f(\lambda\ul{u}) = \lambda T_f(\ul{u})\,\forall \lambda\in \R, \forall \ul{v}\in V$.

Agora temos uma função \[\varphi:\{f\colon B\to W\mid \mbox{$f$ é uma função}\}\longrightarrow \{T\colon V\to W\mid \mbox{$T$ é TL}\}\] dada por $f\mapsto T_f$. Afirmo que $\varphi$ é bijetiva:

Dada uma TL $T:V\to W$, podemos restringir o domínio para $B$ para obter uma função $T|_{B} : B\to W$. Mas $T = \varphi(T|_{B})$.
Suponha que $f,g:B\to W$ são funções tais que $T_f = T_g$. Para todo $\ul{b}\in B$ temos \[f(\ul{b}) = T_f(\ul{b}) = T_g(\ul{b}) = g(\ul{b})\] então $f=g$ e $\varphi$ é injetiva.

◻

Agora sejam $V = \R^m\,,\,W = \R^n$ com elementos escritos como vetores colunas, e \[B = \{E_1\,,\,E_2\,,\,\ldots\,,\,E_m\} = \left\{\begin{pmatrix} 1 \\ 0 \\ 0 \\ \vdots \\ 0 \end{pmatrix}\,,\,\begin{pmatrix} 0 \\ 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix}\,,\,\ldots\,,\,\begin{pmatrix} 0 \\ 0 \\ 0 \\ \vdots \\ 1 \end{pmatrix}\right\}\] a base canônica de $V$. Do teorema, uma transformação linear $T:V\to W$ está determinada completamente pelas imagens dos elementos de $B$. Escreva \[T(E_j) = \begin{pmatrix} a_{1j} \\ a_{2j} \\ \vdots \\ a_{nj} \end{pmatrix}\in W = \R^n.\] Seja $A$ a matriz $n\times m$ cuja $j$-ésima coluna é $T(E_j)$: \[A = \begin{pmatrix} T(E_1) & T(E_2) & \cdots & T(E_m) \end{pmatrix} = \begin{pmatrix} a_{11} & \cdots & a_{1j} & \cdots & a_{1m} \\ a_{21} & \cdots & a_{2j} & \cdots & a_{2m} \\ \vdots & & \vdots & & \vdots \\ a_{n1} & \cdots & a_{nj} & \cdots & a_{nm} \end{pmatrix}.\] Afirmo que $T = T_A$. Para ver isso, basta confirmar que $T_A(E_j) = T(E_j)$ para cada elemento da base de $V$. Mas \[\begin{aligned} T_A(E_j) & = \begin{pmatrix} a_{11} & \cdots & a_{1j} & \cdots & a_{1m} \\ a_{21} & \cdots & a_{2j} & \cdots & a_{2m} \\ \vdots & & \vdots & & \vdots \\ a_{n1} & \cdots & a_{nj} & \cdots & a_{nm} \end{pmatrix}\cdot \begin{pmatrix} 0 \\ \vdots \\ 1 \\ \vdots \\ 0 \end{pmatrix}\quad(j\hbox{-ésima linha}) \\ & = \begin{pmatrix} a_{1j} \\ a_{2j} \\ \vdots \\ a_{nj} \end{pmatrix} \\ & = T(E_j).\qquad\qquad \checkmark \end{aligned}\]

Já que toda matriz $n\times m$ $A$ dá uma TL $T_A:\R^m\to \R^n$ e toda TL $\R^m\to \R^n$ tem a forma $T_A$ para alguma matriz $n\times m$, mostramos de alguma forma que matrizes $n\times m$ e TLs $\R^m\to \R^n$ são “a mesma coisa”. Vamos fazer essa frase cada vez mais precisa.

Definição 42.2 Um isomorfismo $\rho:V\to W$ de espaços vetoriais é uma transformação linear $\rho:V\to W$ bijetiva (Definição 8.3). Quando existir um isomorfismo de $V$ a $W$, diremos que $V,W$ são espaços vetoriais isomorfos.

Pensamos em espaços vetoriais isomorfos como sendo essencialmente iguais (como espaços vetoriais) – o isomorfismo está simplesmente “renomeando” os elementos. Vamos falar mais sobre espaços vetoriais isomorfos depois.

Exemplo 42.3

O espaço vetorial $P_3$ de polinômios de grau menor ou igual a três é isomorfo ao espaço $\R^4$. O isomorfismo é a TL \[T:P_3\to \R^4,\qquad \alpha_0+\alpha_1x+\alpha_2x^2+\alpha_3x^3\mapsto (\alpha_0,\alpha_1,\alpha_2,\alpha_3).\]
O espaço vetorial $M_{2,3}(\R)$ de matrizes $2\times 3$ é isomorfo a $\R^6$; o isomorfismo é \[T:M_{2,3}(\R)\to \R^6,\qquad \begin{pmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \end{pmatrix} \mapsto (a_{11},a_{12},a_{13},a_{21},a_{22},a_{23}).\]

Teorema 42.3 Sejam $V = \R^m$ e $W = \R^n$. A função \[\rho : M_{n,m}(\R) \to \mathcal{L}(V,W)\] dada por $A\mapsto T_A$ é um isomorfismo de espaços vetoriais.

Comprovação. A função $\rho$ é

Pois $A,B\in M_{n,m}(\R)$ com $T_A= T_B$ implica que $T_A(E_j) = T_B(E_j)\,\forall j$. Ou seja, as $j$-ésima colunas de $A,B$ são iguais para cada $j$, logo $A=B$.
Mostramos acima que qualquer TL de $V$ a $W$ tem a forma $T_A$ para alguma matriz $n\times m$ $A$.
Dadas matrizes $A,B$, dizer que $\rho(A+B) = \rho(A) + \rho(B)$ é dizer que $T_{A+B} = T_A + T_B$ como funções $V\to W$. Mas essas funções são iguais se, e somente se, $T_{A+B}(\ul{v}) = (T_A+T_B)(\ul{v})\,\forall \ul{v}\in V$. Vamos lá: \[\begin{align*} T_{A+B}(\ul{v}) & = (A+B)\cdot \ul{v} \\ & = A\ul{v} + B\ul{v} \\ & = T_A(\ul{v}) + T_B(\ul{v}) \\ & = (T_A + T_B)(\ul{v}).\qquad\checkmark \end{align*}\] Exercício: Mostre que $\rho(\lambda A) = \lambda\rho(A)$.

◻

Exemplo 42.4 Encontre as matrizes

$A$ da TL $S:\R^3\to \R^3$ que faz uma reflexão no plano $xy$,
$B$ da TL $T:\R^3\to \R^3$ que faz uma rotação por $90$ graus em torno do eixo $z$,
$C$ da TL que faz $S$ e depois faz $T$.

As colunas da matriz $A$ são as imagens dos vetores da base canônica de $\R^3$. Então vamos pegar um vetor da base canônica e refletir ele no plano $xy$: \[(1,0,0)\mapsto (1,0,0)\] \[(0,1,0)\mapsto (0,1,0)\] \[(0,0,1)\mapsto (0,0,-1).\] A matriz é \[A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{pmatrix}.\]
Para calcular $B$, faremos uma rotação por $90$ graus em torno do eixo $z$ dos vetores da base canônica:

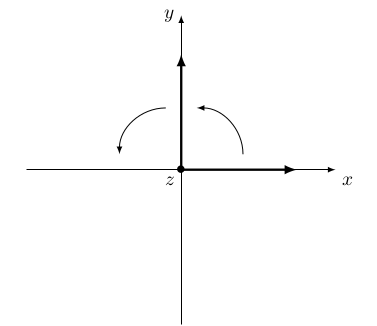
A rotação por 90 graus

\[(1,0,0)\mapsto (0,1,0)\] \[(0,1,0)\mapsto (-1,0,0)\] \[(0,0,1)\mapsto (0,0,1).\] A matriz é \[B = \begin{pmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix}.\]
Para calcular $C$, reflete os vetores da base canônica no plano $xy$ e depois virar eles por $90$ graus em torno do eixo $z$: \[(1,0,0)\xrightarrow{\hbox{refletir}}(1,0,0)\xrightarrow{\hbox{virar}}(0,1,0)\] \[(0,1,0)\xrightarrow{\hbox{refletir}}(0,1,0)\xrightarrow{\hbox{virar}}(-1,0,0)\] \[(0,0,1)\xrightarrow{\hbox{refletir}}(0,0,-1)\xrightarrow{\hbox{virar}}(0,0,-1)\] A matriz é \[C = \begin{pmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & -1 \end{pmatrix}.\]

Observe que \[\begin{aligned} (\hbox{matriz de }T)\cdot(\hbox{matriz de }S) & = B\cdot A \\ & = \begin{pmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{pmatrix} \\ & = \begin{pmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & -1 \end{pmatrix} \\ & = C \\ & = (\hbox{matriz de }T\circ S). \end{aligned}\]

De fato, a matriz da composição de TLs (Definição 8.4) é sempre o produto das matrizes das TLs. Suponha que temos três espaços vetoriais $\R^l, \R^m, \R^n$ com bases canônicas \[\begin{aligned} E_k\quad & ,\quad k\in \{1,\ldots,l\} \\ F_j\quad & ,\quad j\in \{1,\ldots,m\} \\ G_i\quad & ,\quad i\in \{1,\ldots,n\} \end{aligned}\] respetivamente. Suponha que temos TLs \[\R^l \xrightarrow{T_A} \R^m \xrightarrow{T_B} \R^n\] onde $A$ é uma matriz $m\times l$, $B$ é uma matriz $n\times m$, e $T_A, T_B$ são as TLs correspondentes.

Teorema 42.4 A matriz $n\times l$ da composição $T_B\circ T_A$ (Definição 8.4) é a matriz produto $BA$. Ou seja, \[T_B\circ T_A = T_{BA}.\]

Comprovação. ’Observe primeiro que $A$ e $B$ são matrizes $m\times l$ e $n\times m$, respetivamente, portanto o produto $BA$ pode ser calculado e este produto vai ser uma matriz $n\times l$. Seja $\ul v\in \R^l$ considerando como vetor coluna $l\times 1$ e verifiquemos que \[(T_B\circ T_A)(\ul v)= T_B(T_A(v))=T_B(A\ul v)=B(A\ul v)=(BA)\ul v=T_{BA}(\ul v).\] ◻

Então, a conclusão é: “matrizes são transformações lineares entre espaços vetoriais da forma $\R^n$ com respeito às bases canônicas. A composição de tais TLs é dada pela multiplicação das matrizes correspondentes.”

Uma de nossas tarefas principais agora é para generalizar essa frase para quaisquer espaços vetoriais de dimensão finita, e quaisquer bases deles.