40 Bases e dimensão

Bases

A última proposição da semana anterior (\(X\) é LD \(\Longleftrightarrow\) pelo menos um dos vetores de \(X\) é combinação linear dos outros) diz que um conjunto LD é “ineficiente”, no sentido que um vetor em \(X\) já pertence ao subespaço gerado pelos outros, então ele é desnecessário. Um conjunto LI é um conjunto de vetores eficiente, no sentido que TODO vetor de \(X\) é necessário para gerar o subespaço gerado por \(X\). Conjuntos de geradores LI são extremamente importantes e merecem um nome:

Definição 40.1 Seja \(V\) um espaço vetorial. Um subconjunto \(X\) de \(V\) é uma base de \(V\) se

\(V\) é gerado por \(X\),
\(X\) é linearmente independente.

Exemplo 40.1

A base canônica de \(\R^n\) é o conjunto dos \(n\) vetores \[B = \left\{(1,0,0,\ldots,0)\,,\, (0,1,0,\ldots,0)\,,\, \ldots\,,\, (0,\ldots,0,1)\right\}.\] Afirmo que é óbvio que \(B\) gera \(\R^n\) e que \(B\) é LI. Recomendo que confirmar estes fatos. Então, \(B\) é uma base de \(\R^n\).
Mas \(\R^n\) (de fato, qualquer espaço vetorial) tem MUITOS bases diferentes. De um exemplo anterior: \[X = \{(1,1)\,,\,(1,-1)\}\] é uma base de \(\R^2\): Já confirmamos que \(X\) é LI. \(X\) gera \(\R^2\), pois a equação \[\lambda(1,1) + \mu(1,-1) = (a,b)\] tem solução \[\lambda = \frac{a+b}{2}\,,\quad \mu = \frac{a-b}{2}.\]
\(M_{m,n}(\R)\) também tem uma base canônica. Dados \(a\in \{1,\ldots,m\}, b\in \{1,\ldots,n\}\), seja \(E_{ab}\) a matrix \((e_{ij})\) com \(e_{ab} = 1\) e \(e_{ij} = 0\) quando \(i\neq a\) ou \(j\neq b\). O conjunto \(X\) das \(mn\) matrizes \[X = \left\{E_{ab}\,|\,a\in \{1,\ldots,m\}, b\in \{1,\ldots,n\}\right\}\] é uma base de \(M_{m,n}(\R)\). Por exemplo, quando \(m=n=2\), \[X = \left\{\begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}\,,\, \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}\,,\,\begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix}\,,\,\begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix} \right\}.\] Afirmo de novo que \(X\) obviamente gera \(M_{m,n}(\R)\) e é LI, logo \(X\) é uma base de \(M_{m,n}(\R)\).
Já observamos que o espaço vetorial \(\R[x]\) dos polinômios com coeficientes em \(\R\) é gerado pelo conjunto \[X = \{1,\,x,\,x^2,\,x^3,\,\ldots\}.\] Mas \(X\) é LI: uma combinação linear de elementos de \(X\) é \[a_nx^n + \cdots + a_1x + a_0\] com \(a_0,\ldots,a_n\in \R\). Este polinômio é \(\ul{0}\) se, e somente se, todos os \(a_i\) são \(0\). Entaõ \(X\) é LI.

Segue que \(X\) é uma base de \(\R[x]\). Diferente dos exemplos anteriores, observe que \(X\) não é um conjunto finito.
O espaço vetorial \(\{\ul{0}\}\) tem base \(\varnothing\).

Coordenadas

O seguinte resultado explica porque bases são tão importantes na teoria dos espaços vetoriais.

Teorema 40.1 Se \(B\) é uma base de um espaço vetorial \(V\), então todo elemento de \(V\) pode ser escrito unicamente como combinação linear de elementos em \(B\).

Comprovação. A definição da base implica que todo elemento de \(V\) pode ser escrito como combinação linear de elementos de \(B\). Assuma que um vetor \(\ul v\) pode ser escrito de duas maneiras: \[\ul v=\alpha_1 \ul{b_1}+\cdots+\alpha_k \ul{b_k}=\beta_1\ul{b_1}+\cdots+\beta_k\ul{b_k}\] com \(\ul{b_1},\ldots,\ul{b_k}\in B\) e \(\alpha_1,\ldots,\alpha_k,\beta_1,\ldots,\beta_k\in\R\). Subtraindo o lado direito do lado esquerdo, obtemos que \[\ul 0=(\alpha_1-\beta_1) \ul{b_1}+\cdots+(\alpha_k-\beta_k) \ul{b_k}.\] Mas, como \(B\) é uma base, os vetores \(\ul{b_1},\ldots,\ul{b_k}\) são LI e isto significa (pela definição de ser LI) que \[(\alpha_1-\beta_1)=\cdots=(\alpha_k-\beta_k)=0;\] ou seja, \(\alpha_i=\beta_i\) vale para todo \(i\). Obbtivemos assim que a expressão de \(\ul v\) como combinação linear de elementos de \(B\) é única. ◻

Definição 40.2 Seja \(B\) uma base de um espaço vetorial \(V\) e seja \(\ul v\in V\). Escreva o vetor \(\ul v\) como uma combinação linear \(\ul v=\alpha_1\ul{b_1}+\cdots+\alpha_k\ul{b_k}\) de elementos de \(B\). Os escalares \(\alpha_1,\ldots,\alpha_k\) são chamadas de coordenadas do vetor \(\ul v\) relativas à base \(B\). O vetor \((\alpha_1,\ldots,\alpha_k)\) é chamado de vetor das coordenadas de \(\ul{v}\) na base \(B\) e será denotado por \(\ul v_B\).

Como está enfatizado na definição acima, as coordenadas de um vetor \(v\) dependem da base escolhida.

Exemplo 40.2 Considere \(V=\R^3\). Considere a base canônica \(B_1=\{(1,0,0),(0,1,0),(0,0,1)\}\) de \(V\) e considere também a base \(B_2=\{(1,1,0),(1,0,1),(0,1,1)\}\) de \(V\). Seja \(\ul v=(1,-1,1)\). O vetor \(\ul v\) pode ser escrito como combinação linear nestas bases na maneira seguinte: \[\ul v=1\cdot(1,0,0)-1\cdot(0,1,0)+1\cdot(0,0,1)=(-1/2)(1,1,0)+(3/2)(1,0,1)-(1/2)(0,1,1).\] Então as coordenadas de \(\ul v\) são \(1\), \(-1\), \(1\) relativas à base \(B_1\), enquanto as coordenadas relativas à base \(B_2\) são \(-1/2\), \(3/2\), \(-1/2\).

Existência de bases

Definição 40.3 O espaço vetorial \(V\) é finitamente gerado se existir um subconjunto finito \(X\) de \(V\) que gera \(V\).

O seguinte resultado vale para espaços vetoriais quaisquer, mas a prova usa técnicas da teoria dos conjuntos que a gente não possui.

Teorema 40.2 Sejam \(V\) um espaço vetorial finitamente gerado e \(X\) um conjunto finito de geradores de \(V\). Algum subconjunto de \(X\) é uma base de \(V\).

Comprovação. O espaço vetorial \(\{\ul{0}\}\) possui a base \(\varnothing\), então vamos supor que \(V\neq \{\ul{0}\}\). Seja \(B = \{\ul{b_1}, \ldots ,\ul{b_n}\}\) um subconjunto maximal LI de \(X\): isto é, \(B\subseteq X\) é LI, mas quando colocar qualquer outro elemento de \(X\), então o conjunto obtido será LD.

Afirmamos que qualquer \(\ul{v}\in X\) é combinação linear de elementos de \(B\): os elementos de \(B\) obviamente são, então seja \(\ul{v} \in X\backslash B\). O conjunto \(B\cup\{\ul{v}\}\) é LD (pois \(B\) é maximal LI), então existem números \(\lambda, a_1,\ldots,a_n\) nem todos \(0\), tais que \[\lambda\ul{v} + a_1\ul{b_1} + \cdots + a_n\ul{b_n} = \ul{0}.\] Se \(\lambda\) fosse \(0\), teríamos que \[a_1\ul{b_1} + \cdots + a_n\ul{b_n} = \ul{0}\] com nem todo \(a_i = 0\) – impossível, pois \(B\) é LI. Então, \(\lambda\neq 0\) e podemos rearranjar para obter \[\ul{v} = -\frac{a_1}{\lambda}\ul{b_1} - \cdots - \frac{a_n}{\lambda}\ul{b_n}.\] Já que todo elemento de \(X\) é combinação linear dos elementos de \(B\), o subespaço gerado por \(B\) contém o subespaço gerado por \(X\), mas esse é \(V\). Logo \(B\) gera \(V\). Então, \(B\) é um conjunto LI de geradores de \(V\), ou seja, uma base de \(V\). ◻

Corolário 40.1 Qualquer espaço vetorial finitamente gerado possui uma base finita.

Comprovação. Seja \(X\) um conjunto finito de geradores de \(V\). Pelo teorema, algum subconjunto de \(X\) é uma base finita de \(V\). ◻

Dimensão

Em princípio, pode acontecer que um espaço vetorial possui uma base com 3 elementos, e outra base com 4 elementos. Vamos mostrar que isso não acontece. Quaisquer duas bases de um espaço vetorial finitamente gerado têm o mesmo tamanho.

Proposição 40.1 Seja \(B = \{\ul{b_1},\ldots,\ul{b_n}\}\) uma base de \(V\) com \(n\) elementos. Qualquer subconjunto \(X\) de \(V\) com mais que \(n\) elementos é LD.

Comprovação. Seja \(Y = \{\ul{v_1}, \ldots,\ul{v_{n+1}}\}\) um subconjunto de \(X\) com \(n+1\) elementos. Vamos mostrar que \(Y\) é LD (logo \(X\) também a é). Temos que mostrar que a equação \[\lambda_1\ul{v_1} + \cdots + \lambda_{n+1}\ul{v_{n+1}} = \ul{0}\qquad (*)\] possui solução não trivial. Já que \(B\) gera \(V\), cada \(\ul{v_i}\) é combinação linear dos elementos de \(B\): \[\begin{aligned} \ul{v_1} & = a_{1,1}\ul{b_1} + \cdots + a_{n,1}\ul{b_n} \\ \ul{v_2} & = a_{1,2}\ul{b_1} + \cdots + a_{n,2}\ul{b_n} \\ & \quad\qquad\vdots \\ \ul{v_{n+1}} & = a_{1,{n+1}}\ul{b_1} + \cdots + a_{n,{n+1}}\ul{b_n} \\ \end{aligned}\] Substituindo estas expressões em \((*)\) e colocando os \(\ul{b_i}\) em evidência, obtemos a equação \[(a_{1,1}\lambda_1 + \cdots + a_{1,{n+1}}\lambda_{n+1})\ul{b_1} + \cdots + (a_{n,1}\lambda_1 + \cdots + a_{n,{n+1}}\lambda_{n+1})\ul{b_n} = \ul{0}.\]

Mas \(B\) é LI, logo obtemos as equações \[\begin{aligned} a_{1,1}\lambda_1 + \cdots + a_{1,{n+1}}\lambda_{n+1} & = 0 \\ \vdots\quad\qquad & \\ a_{n,1}\lambda_1 + \cdots + a_{n,{n+1}}\lambda_{n+1} & = 0 \end{aligned}\] Mas este é um sistema homogêneo com \(n\) equações e \(n+1\) variáveis. Então ele possui uma solução não trivial, como a gente queria. ◻

Teorema 40.3 Seja \(B\) uma base finita do espaço vetorial \(V\) é seja \(C\) outra base de \(V\). Então \(|C| = |B|\).

Comprovação. Já que \(B\) é uma base de \(V\) e \(C\) é LI, segue da proposição que \(|C|\leqslant |B|\). Mas agora \(C\) é uma base finita e \(B\) é LI, então \(|B|\leqslant|C|\) pela proposição de novo. Logo \(|B| = |C|\). ◻

Exemplo 40.3

O subconjunto de \(M_{2,2}(\R)\) \[X = \left\{\begin{pmatrix} 1 & 1 \\ 3 & 6 \end{pmatrix}\,,\, \begin{pmatrix} 2 & 0 \\ 8 & 5 \end{pmatrix}\,,\,\begin{pmatrix} 6 & -2 \\ 3 & 0 \end{pmatrix}\,,\,\begin{pmatrix} 1 & 1 \\ 1 & 1 \end{pmatrix}\,,\,\begin{pmatrix} -2 & 3 \\ 2 & 5 \end{pmatrix} \right\}\] é LI ou LD?

R: Poderia resolver essa questão usando sistemas lineares, mas seria chato. Em vez disso: já observamos que \(M_{2,2}(\R)\) possui uma base com quatro elementos \[\left\{\begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}\,,\, \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}\,,\,\begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix}\,,\,\begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix} \right\},\] logo qualquer conjunto com mais que 4 elementos é LD. Já que \(|X| = 5\), acabou – \(X\) é LD.
Mostre que o espaço vetorial \(\R[x]\) não possui uma base finita.

R: Até agora, sabemos que \(\R[x]\) possui pelo menos uma base infinita, nomeadamente \[X = \{1,x,x^2,x^3,\ldots\}.\] Suponha que \(\R[x]\) também possuísse uma base finita \(B\). Mas o teorema diz então que \(|X| = |B| < \infty\), uma contradição.

Já que o tamanho de uma base finita de um espaço vetorial \(V\) é independente da base, este número é um invariante do espaço vetorial.

Definição 40.4 Seja \(V\) um espaço vetorial com base finita \(B\). A dimensão de \(V\) é a cardinalidade de \(B\). Se \(B\) possui \(n\) elementos, escrevemos \[\dim(V) = n.\]

Caso \(V\) não possuir uma base finita, diremos que \(V\) tem dimensão infinita.

Exemplo 40.4

O único espaço vetorial com dimensão \(0\) é \(\{\ul{0}\}\) (já que a base \(\varnothing\) tem tamanho \(0\)).
A base canônica de \(\R^n\) possui \(n\) elementos, então \(\dim(\R^n) = n\).
A base canônica de \(M_{m,n}(\R)\) consiste das \(mn\) matrizes \(E_{ij}\) (tendo \(1\) na posição \(i,j\) e \(0\) fora disso). Logo \(\dim(M_{m,n}(\R)) = mn\). Em particular, o espaço das matrizes quadradas \(M_{n,n}(\R)\) tem dimensão \(n^2\).
Os espaços \(\R[x]\) e \(\mathcal{F}(\R,\R)\) têm dimensão infinita.
O subconjunto de \(M_{2,3}(\R)\): \[X = \left\{ \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1\end{pmatrix}\,,\, \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix}\,,\, \begin{pmatrix} 0 & 0 & 2 \\ 0 & 1 & 0 \end{pmatrix} \right\}\] é LI. Segue que o subespaço gerado por \(X\) \[W = \left\{\left. \begin{pmatrix} a & b & 2c \\ 0 & c & a \end{pmatrix}\,\right|\, a,b,c\in \R \right\}\] tem base \(X\). Já que \(|X| = 3\), temos \(\dim(W) = 3\).
Exercício: Seja \(AX=\ul{0}\) um sistema homogêneo. Mostre que a dimensão do conjunto solução do sistema é o número de variáveis livres do sistema.

Existe um espaço vetorial de dimensão \(5\) tendo subespaço de dimensão \(6\)? Não!

Proposição 40.2 Sejam \(V\) um espaço vetorial de dimensão finita e \(W\) um subespaço de \(V\).

\(\dim(W)\leqslant \dim(V)\),
Se \(\dim(W) = \dim(V)\), então \(W=V\).

Comprovação.

Suponha (procurando contradição) que \[\dim(W) = m > \dim(V).\] Então \(W\) possui uma base \(B = \{\ul{w_1}\,,\,\ul{w_2}\,,\,\ldots\,,\,\ul{w_m}\}\) de \(m\) elementos. Em particular, \(B\) é um subconjunto LI de \(V\) com mais que \(\dim(V)\) elementos. Mas já mostramos que qualquer subconjunto de \(V\) com mais que \(\dim(V)\) elementos é LD, então isso não é possível.
Suponha que \(W\leqslant V\) tem dimensão \(n = \dim(V)\). Queremos mostrar que \(W=V\). Vamos pegar \(\ul{v}\in V\) qualquer e mostrar que \(\ul{v}\in W\). Seja \(B = \{\ul{w_1}\,,\,\ul{w_2}\,,\,\ldots\,,\,\ul{w_n}\}\) uma base de \(W\). Já que \(\dim(V) = n\), o conjunto \[\{\ul{w_1}\,,\,\ul{w_2}\,,\,\ldots\,,\,\ul{w_n}, \ul{v}\}\] é LD, então existem \(a_1,\ldots,a_n,b\in \R\) nem todos \(0\) tais que \[a_1\ul{w_1} + a_2\ul{w_2} + \cdots + a_n\ul{w_n} + b\ul{v} = \ul{0}.\] Mas \(b\neq 0\), pois se fosse \(0\), teríamos uma solução não trivial que envolve somente os \(\ul{w_i}\) – impossível, pois \(B\) é LI. Então, rearranjando, \[\ul{v} = -\left( \frac{a_1}{b}\ul{w_1} + \frac{a_2}{b}\ul{w_2} + \cdots + \frac{a_n}{b}\ul{w_n} \right),\] mostrando que \(\ul{v}\) é combinação linear de elementos de \(W\), logo \(\ul{v}\in W\).

◻

Suponha que temos um espaço \(V\) com dimensão \(n\). Queremos saber se algum subconjunto \(B\) é uma base de \(V\):

Vai ter que ter \(n\) elementos, pois qualquer base tem.
Vai ter que gerar \(V\).
Vai ter que ser LI.

De fato, basta confirmar quaisquer duas dessas coisas:

Teorema 40.4 Sejam \(V\) um espaço vetorial de dimensão \(n\) e \(B\) um subconjunto de \(V\). Se \(B\) tem qualquer duas das propriedades \(1,2,3\) acima, então \(B\) é uma base de \(V\).

Comprovação. Suponha que \(B\) satisfaz:

Propriedades 2. e 3.: Então \(B\) é uma base pela definição de base.
Propriedades 1. e 2.: Já que \(B\) gera \(V\), sabemos que algum subconjunto \(B'\) de \(B\) é base de \(V\). Se \(B\) não for LI, \(B'\neq B\), então \(V\) tem base de \(<n\) elementos – contradição.
Propriedades 1. e 3.: Já que \(B\) é LI, ele é uma base do subespaço gerado por \(B\), e este subespaço tem dimensão \(n\). Mas o único subespaço de \(V\) com dimensão \(n\) é \(V\), então \(B\) gera \(V\).

◻

Exercício 40.1 Seja \(V\) um espaço vetorial de dimensão finita. Já mostramos que qualquer subconjunto finito de geradores de \(V\) pode ser “diminuido” para uma base de \(V\). Mostre a outra direção: que qualquer subconjunto LI de \(V\) pode ser estendido para uma base de \(V\). Isto é, se \(X\) é LI, então existe uma base \(B\) de \(V\) com \(X\subseteq B\).

A dimensão da soma

Teorema 40.5 Sejam \(W,Y\) subespaços do espaço vetorial de dimensão finita \(V\). Então \[\dim(W+Y) = \dim(W) + \dim(Y) - \dim(W\cap Y).\]

Comprovação. Seja \(I = \{\ul{v_1}\,,\,\ldots\,,\,\ul{v_a}\}\) uma base de \(W\cap Y\). Já que \(I\subseteq W\) é LI, pelo exercício podemos estender \(I\) para uma base \(B=\{\ul{v_1}\,,\,\ldots\,,\,\ul{v_a}\,,\,\ul{w_1}\,,\,\ldots\,,\,\ul{w_b}\}\) de \(W\), e similarmente estender \(I\) para uma base \(C=\{\ul{v_1}\,,\,\ldots\,,\,\ul{v_a}\,,\,\ul{y_1}\,,\,\ldots\,,\,\ul{y_c}\}\) de \(Y\). Já que \(B\) gera \(W\) e \(C\) gera \(Y\), \(B\cup C\) gera \(W+Y\). Vamos confirmar que \(B\cup C\) é LI: suponha que \[\alpha_1\ul{v_1} + \cdots + \alpha_a\ul{v_a} + \beta_1\ul{w_1} + \cdots + \beta_b\ul{w_b} + \gamma_1\ul{y_1} + \cdots + \gamma_c\ul{y_c} = \ul{0}.\quad(*)\] Rearranjando, \[\gamma_1\ul{y_1} + \cdots + \gamma_c\ul{y_c} = -\left(\alpha_1\ul{v_1} + \cdots + \alpha_a\ul{v_a} + \beta_1\ul{w_1} + \cdots + \beta_b\ul{w_b}\right)\] pertence a \(W\cap Y\), logo existem \(\delta_1,\ldots,\delta_a\) tais que \[\gamma_1\ul{y_1} + \cdots + \gamma_c\ul{y_c} = \delta_1\ul{v_1} + \cdots + \delta_a\ul{v_a}.\] Mas rearranjando de novo, \[\gamma_1\ul{y_1} + \cdots + \gamma_c\ul{y_c} - \delta_1\ul{v_1} - \cdots - \delta_a\ul{v_a} = \ul{0},\] então cada \(\gamma_i = 0\), pois \(C\) é uma base, logo LI (cada \(\delta_i=0\) também, mas não precisamos disso). Jogando \(\gamma_i=0\,\forall i\) na equação \((*)\), obtemos \[\alpha_1\ul{v_1} + \cdots + \alpha_a\ul{v_a} + \beta_1\ul{w_1} + \cdots + \beta_b\ul{w_b} = \ul{0},\] mostrando que \(\alpha_i = 0\,\forall i\) e \(\beta_i = 0\,\forall i\), pois \(B\) é LI. Então \((*)\) possui somente a solução trivial, logo \(B\cup C\) é uma base de \(W+Y\). Finalmente, \[\begin{aligned} \dim(W+Y) & = |B\cup C| \\ & = a + b + c \\ & = (a + b) + (c + a) - a \\ & = |B| + |C| - |I| \\ & = \dim(W) + \dim(Y) - \dim(W\cap Y). \end{aligned}\] ◻

Corolário 40.2 Sejam \(V\) um espaço vetorial e \(W,Y\) dois subespaços tais que \[V = W\oplus Y.\] Então \[\dim(V) = \dim(W) + \dim(Y).\]

Comprovação. Imediato do teorema, pois \(\dim(W\cap Y) = \dim(\{\ul{0}\}) = 0\). ◻

Definição 40.5 Seja \(W\) um subespaço do espaço vetorial \(V\). Um complemento de \(W\) em \(V\) é um subespaço \(Y\) de \(V\) tal que \(V = W\oplus Y\).

Corolário 40.3 Sejam \(V\) um espaço vetorial de dimensão finita e \(W\) um subespaço de \(V\). Existe um complemento de \(W\) em \(V\).

Comprovação. Seja \(\{\ul{w_1}\,,\,\ldots,\ul{w_a}\}\) uma base de \(W\) e estenda ela para uma base \[\{\ul{w_1}\,,\,\ldots\,,\,\ul{w_a}\,,\,\ul{y_1}\,,\,\ldots\,,,\,\ul{y_b}\}\] de \(V\). Seja \(Y\) o subespaço gerado por \(\{\ul{y_1}\,,\,\ldots\,,\,\ul{y_b}\}\). Então \(V = W + Y\). Mas \(\dim(V)=a+b\) então pelo teorema \[\begin{aligned} \dim(W\cap Y) & = \dim(W) + \dim(Y) - \dim(W+Y) \\ & = a + b - (a+b) \\ & = 0, \end{aligned}\] logo \(W\cap Y = \{\ul{0}\}\) e \(V = W\oplus Y\). ◻

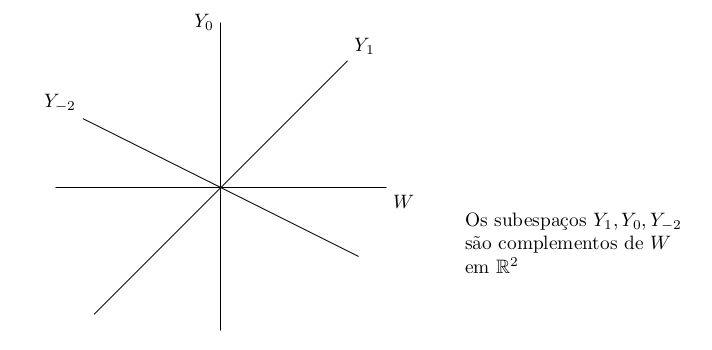
Cuidado: Um subespaço \(W\) geralmente possui MUITOS complementos distintos:

Exemplo 40.5 (Exercício) Seja \(V = \R^2\) e \(W\) o subespaço com base \(\{(1,0)\}\). Então os subespaços \[Y_{b}\quad\hbox{tendo base}\quad \{(b,1)\}\] são distintos para todo \(b\in \R\), e qualquer \(Y_b\) é complemento de \(W\) em \(\R^2\).