64 Exercícios: Bloco 1

Os seguintes exercícios são recomendados para o Bloco I das apostilas de Álgebra Linear II. Salvo indicação em contrário, as soluções foram geradas utilizando o modelo GPT-4o por meio da interface disponibilizada pelo GitHub Copilot no editor VS Code e foram editadas por Csaba. Caso, haja algum erro avise por gentileza pelo email csaba.schneider@gmail.com ou corriga diretamente no código fonte.

Exercício 64.1 Seja $\F$ um corpo. Mostre que

O elemento neutro aditivo $0_\F$ é único.
O elemento neutro multiplicativo $1_\F$ é único.
Se $a\in\F$, então o negativo $-a$ é único.
Se $a\in\F\setminus\{0_\F\}$, então o inverso $a^{-1}$ é único.

Solução:

Apresentamos a solução dos itens 1. e 3. O leitor poderá fazer itens 2. e 4.

O elemento neutro aditivo $0_\F$ é único. Suponha que existam dois elementos neutros aditivos $0_\F$ e $0'_\F$. Então, por definição de elemento neutro aditivo, temos que $0_\F + 0'_\F = 0'_\F$ e $0_\F + 0'_\F = 0_\F$. Portanto, $0_\F = 0'_\F$, mostrando que o elemento neutro aditivo é único.
Se $a\in\F$, então o negativo $-a$ é único. Suponha que existam dois negativos de $a$, denotados por $-a$ e $-a'$. Então, usando a definição do negativo e a associatividade, \[ -a = -a+(a+(-a'))=(-a+a)+(-a')=-a'. \]

Exercício 64.2 Seja $\F$ um corpo. Demonstre as seguintes leis cancelativas.

Se $a+b=a+c$, então $b=c$ para todo $a,b,c\in\F$.
Se $ab=ac$, então $b=c$ para todo $a,b,c\in\F$ com $a\neq 0_\F$.

Solução:

Suponha que $a + b = a + c$. Podemos adicionar o elemento neutro aditivo $-a$ em ambos os lados da equação: \[ -a + (a + b) = -a + (a + c). \] Pela associatividade da adição, temos: \[ (-a + a) + b = (-a + a) + c. \] Como $-a + a = 0_\F$, obtemos: \[ 0_\F + b = 0_\F + c. \] E, pela propriedade do elemento neutro aditivo, concluímos que $b = c$.
Suponha que $ab = ac$ com $a \neq 0_\F$. Podemos multiplicar ambos os lados da equação pelo inverso multiplicativo de $a$, denotado por $a^{-1}$: \[ a^{-1}(ab) = a^{-1}(ac). \] Pela associatividade da multiplicação, temos: \[ (a^{-1}a)b = (a^{-1}a)c. \] Como $a^{-1}a = 1_\F$, obtemos: \[ 1_\F b = 1_\F c. \] E, pela propriedade do elemento neutro multiplicativo, concluímos que $b = c$.

Exercício 64.3 Decide quais dos seguintes conjuntos são corpos (com as operações $+$ e $\cdot$ usuais). Justifique sua resposta.

$\Z[i]=\{a+bi\mid a,b\in\Z\}$ (como subconjunto de $\C$).
$\Q[i]=\{a+bi\mid a,b\in\Q\}$ (como subconjunto de $\C$).
$\Z_{10}=\{0,\ldots,9\}$ com as operações mod $10$.
\[ \left\{\begin{pmatrix} 0 & 0 \\ 0 & 0\end{pmatrix}, \begin{pmatrix} 1 & 0 \\ 0 & 1\end{pmatrix} \begin{pmatrix} 0 & 1 \\ 1 & 1\end{pmatrix} \begin{pmatrix} 1 & 1 \\ 1 & 0\end{pmatrix}\right\} \] considerado como subconjunto de $M_2(\Z_2)$.

Solução:

$\Z[i]$ não é um corpo. Embora $\Z[i]$ seja fechado sob adição e multiplicação, ele não é fechado sob inversão multiplicativa. Por exemplo, o inverso de $1 + i$ em $\C$ é $\frac{1}{2}(1 - i)$, que não está em $\Z[i]$.
$\Q[i]$ é um corpo. $\Q[i]$ é fechado sob adição, multiplicação e inversão multiplicativa. Para qualquer $a + bi \in \Q[i]$ com $a, b \in \Q$ e $a + bi \neq 0$, o inverso multiplicativo é \[ \frac{a}{a^2 + b^2} - \frac{b}{a^2 + b^2}i, \] que também está em $\Q[i]$.
$\Z_{10}$ não é um corpo. Embora $\Z_{10}$ seja fechado sob adição e multiplicação módulo 10, ele não possui inversos multiplicativos para todos os elementos não nulos. Por exemplo, 2 não tem inverso multiplicativo em $\Z_{10}$.
O conjunto dado é um corpo. Ele contém quatro matrizes $2 \times 2$ sobre $\Z_2$ e é fechado sob adição e multiplicação de matrizes. Além disso, cada elemento não nulo tem um inverso multiplicativo. Por exemplo, o inverso de \[ \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \] é ele mesmo, o inverso de \[ \begin{pmatrix} 0 & 1 \\ 1 & 1 \end{pmatrix} \] é \[ \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix} \] e vice-versa. Portanto, todas as propriedades de um corpo são satisfeitas.

Exercício 64.4 A caraterística de um corpo $\F$ é definida na seguinte forma. Se não existir um número $n\geq 1$ tal que $1+\cdots+1=0$ (tomando $n$ cópias de $1$), então a caraterística de $\F$ é zero. Se existir tal $n$, então a caraterística de $\F$ é o menor tal $n$. Mostre que a caraterística de um corpo ou é zero ou é um número primo.

Solução:

Seja $\F$ um corpo e suponha que a característica de $\F$ não é zero. Então, existe um número $n \geq 1$ tal que $1 + 1 + \cdots + 1 = 0$ (com $n$ cópias de $1$). Seja $n$ o menor tal número. Vamos mostrar que $n$ é primo.

Suponha, por contradição, que $n$ não é primo. Então, existem inteiros $a, b \geq 2$ tais que $n = ab$. Considere a soma \[ (1 + 1 + \cdots + 1)(1 + 1 + \cdots + 1) \] onde cada parêntese contém $a$ e $b$ cópias de $1$, respectivamente. Pela associatividade e comutatividade da adição, temos \[ (1 + 1 + \cdots + 1)(1 + 1 + \cdots + 1) = ab = n = 0. \] Portanto, temos \[ (1 + 1 + \cdots + 1) = 0 \quad \text{ou} \quad (1 + 1 + \cdots + 1) = 0, \] onde cada parêntese contém $a$ ou $b$ cópias de $1$, respectivamente. Isso contradiz a minimalidade de $n$, pois $a, b < n$.

Portanto, $n$ deve ser primo. Concluímos que a característica de um corpo ou é zero ou é um número primo.

Exercício 64.5 Seja $V$ um espaço vetorial sobre um corpo $\F$.

Mostre que o vetor nulo $0_V$ é único.
Mostre que o negativo $-v$ é único para todo $v\in V$.
Mostre que $\alpha v=0_V$ se e somente se $\alpha=0_\F$ ou $v=0_V$.
Mostre que $(-1_\F)\cdot v=-v$ para todo $v\in V$.

Exercício 64.6 Seja $\F$ um corpo, $n\in\N$, $X=\{1,\ldots,n\}$, e seja $\mbox{Func}(X,\F)=\{f:X\to\F\}$ o $\F$-espaço vetorial das funções de $X$ para $\F$. Para $i\in X$, defina \[ f_i:X\to \F,\quad f_i(j)=\left\{\begin{array}{ll}1\mbox{ caso $i=j$}\\0\mbox{ caso $i\neq j$} \end{array}\right.\quad \mbox{para todo $j\in X$}. \] Mostre que $\{f_1,\ldots,f_n\}$ é uma base de $\mbox{Func}(X,\F)$.

Solução:

Para mostrar que $\{f_1, \ldots, f_n\}$ é L.I., considere uma combinação linear arbitrária dos elementos de $\{f_1, \ldots, f_n\}$ que resulta no vetor nulo: \[ \alpha_1 f_1 + \alpha_2 f_2 + \cdots + \alpha_n f_n = 0, \] onde $\alpha_1, \alpha_2, \ldots, \alpha_n \in \F$. Para cada $j \in X$, temos: \[ (\alpha_1 f_1 + \alpha_2 f_2 + \cdots + \alpha_n f_n)(j) = 0. \] Por definição de $f_i$, isso se torna: \[ \alpha_1 f_1(j) + \alpha_2 f_2(j) + \cdots + \alpha_n f_n(j) = 0. \] Note que $f_i(j) = 1$ se $i = j$ e $f_i(j) = 0$ se $i \neq j$. Portanto, para cada $j \in X$, a equação acima se reduz a: \[ \alpha_j = 0. \] Como isso é válido para todo $j \in X$, concluímos que $\alpha_1 = \alpha_2 = \cdots = \alpha_n = 0$. Portanto, $\{f_1, \ldots, f_n\}$ é L.I.

Para mostrar que $\{f_1, \ldots, f_n\}$ é um sistema gerador de $\mbox{Func}(X, \F)$, precisamos mostrar que qualquer função $f \in \mbox{Func}(X, \F)$ pode ser escrita como uma combinação linear dos elementos de $\{f_1, \ldots, f_n\}$.

Seja $f \in \mbox{Func}(X, \F)$. Para cada $j \in X$, defina $\alpha_j = f(j)$. Então, podemos escrever $f$ como: \[ f = \alpha_1 f_1 + \alpha_2 f_2 + \cdots + \alpha_n f_n. \] Para ver isso, considere qualquer $i \in X$. Então, \[ (\alpha_1 f_1 + \alpha_2 f_2 + \cdots + \alpha_n f_n)(i) = \alpha_1 f_1(i) + \alpha_2 f_2(i) + \cdots + \alpha_n f_n(i). \] Por definição de $f_i$, temos $f_i(i) = 1$ e $f_i(j) = 0$ para $j \neq i$. Portanto, a expressão acima se reduz a: \[ \alpha_i f_i(i) = \alpha_i \cdot 1 = \alpha_i. \] Como $\alpha_i = f(i)$, obtemos: \[ (\alpha_1 f_1 + \alpha_2 f_2 + \cdots + \alpha_n f_n)(i) = f(i). \] Como isso é válido para todo $i \in X$, concluímos que: \[ f = \alpha_1 f_1 + \alpha_2 f_2 + \cdots + \alpha_n f_n. \] Portanto, $\{f_1, \ldots, f_n\}$ é um sistema gerador de $\mbox{Func}(X, \F)$.

Exercício 64.7 Considere o espaço $\mbox{Func}(X,\F)$ como no Exercício 64.6, mas agora ponha $X=\N$. Para todo $i\in\N$, defina $f_i$ na mesma forma como no Exercício 64.6 que pode dizer sobre o conjunto $\{f_1,f_2,f_3,\ldots\}$? Ele é L.I.? Ele é gerador? Ele é base?

Solução:

O conjunto $\{f_1, f_2, f_3, \ldots\}$ é L.I. Para ver isso, considere uma combinação linear finita arbitrária dos elementos de $\{f_1, f_2, f_3, \ldots\}$ que resulta no vetor nulo: \[ \alpha_1 f_1 + \alpha_2 f_2 + \alpha_3 f_3 + \cdots + \alpha_k f_k = 0, \] onde $\alpha_1, \alpha_2, \alpha_3, \ldots, \alpha_k \in \F$. Para cada $j \in \{1, 2, \ldots, k\}$, temos: \[ (\alpha_1 f_1 + \alpha_2 f_2 + \alpha_3 f_3 + \cdots + \alpha_k f_k)(j) = 0. \] Por definição de $f_i$, isso se torna: \[ \alpha_1 f_1(j) + \alpha_2 f_2(j) + \alpha_3 f_3(j) + \cdots + \alpha_k f_k(j) = 0. \] Note que $f_i(j) = 1$ se $i = j$ e $f_i(j) = 0$ se $i \neq j$. Portanto, para cada $j \in \{1, 2, \ldots, k\}$, a equação acima se reduz a: \[ \alpha_j = 0. \] Como isso é válido para todo $j \in \{1, 2, \ldots, k\}$, concluímos que $\alpha_1 = \alpha_2 = \alpha_3 = \cdots = \alpha_k = 0$. Portanto, $\{f_1, f_2, f_3, \ldots\}$ é L.I.

No entanto, $\{f_1, f_2, f_3, \ldots\}$ não é um sistema gerador de $\mbox{Func}(\N, \F)$. Para ver isso, considere uma função $f \in \mbox{Func}(\N, \F)$ tal que $f(i) = 1$ para todo $i \in \N$. Não existe uma combinação linear finita dos elementos de $\{f_1, f_2, f_3, \ldots\}$ que resulta em $f$, pois qualquer combinação linear finita de $f_i$ terá apenas um número finito de entradas não nulas, enquanto $f$ tem infinitas entradas não nulas.

Portanto, $\{f_1, f_2, f_3, \ldots\}$ não é uma base de $\mbox{Func}(\N, \F)$, pois não é um sistema gerador.

Exercício 64.8 Usando o Lema de Zorn, demonstre as seguintes afirmações em um espaço vetorial $V$ não nulo qualquer.

Se $X\subseteq V$ é um conjunto L.I., então existe uma base $\overline X\subseteq V$ tal que $X\subseteq \overline X$.
Se $X\subseteq V$ é um conjunto gerador, então existe uma base $\widetilde X\subseteq V$ tal que $\widetilde X\subseteq X$.

Solução:

Seja $X \subseteq V$ um conjunto L.I. Considere a coleção $\mathcal{C}$ de todos os conjuntos L.I. em $V$ que contêm $X$. Note que $\mathcal{C}$ é não vazia, pois $X \in \mathcal{C}$. Ordenamos $\mathcal{C}$ por inclusão. Seja $\{Y_i\}_{i \in I}$ uma cadeia em $\mathcal{C}$. Defina $Y = \bigcup_{i \in I} Y_i$. Usando o argumento na aula, pode-se verificar que $Y$ é L.I. e contém $X$. Portanto, $Y \in \mathcal{C}$, mostrando que toda cadeia em $\mathcal{C}$ tem uma cota superior em $\mathcal{C}$. Pelo Lema de Zorn, $\mathcal{C}$ tem um elemento maximal, denotado por $\overline{X}$. Mostraremos que $\overline{X}$ é uma base de $V$. Suponha, por contradição, que $\overline{X}$ não é um sistema gerador de $V$. Então, existe $v \in V \setminus \overline{X}$ tal que $\overline{X} \cup \{v\}$ é L.I., contradizendo a maximalidade de $\overline{X}$. Portanto, $\overline{X}$ é uma base de $V$ que contém $X$.
Seja $X \subseteq V$ um conjunto gerador. Considere a coleção $\mathcal{C}$ de todos os subconjuntos de $X$ que são L.I. Ordenamos $\mathcal{C}$ por inclusão. O resto do argumento é como no item 1 e deixamos ao leitor.

Exercício 64.9 Considere o conjunto $X=\{(1,-1,0,0),(0,1,-1,0,),(0,0,1,-1),(1,0,-1,0)\}\subseteq\R^4$.

Mostre que $X$ não é sistema gerador de $\R^4$.
Ache todos os subconjuntos L.I. de $X$.

Exercício 64.10 Se $\F$ é corpo e $k\geq 1$, defina \[ \F[x]_k=\{f\in\F[x]\mid \mbox{grau}f\leq k\}. \] Considere $X=\{1+x+x^2+x^3,1-x+x^2+x^3,1+x-x^2+x^3\}\subseteq \R[x]_3$.

Mostre que $X$ é L.I.
Ache uma base $\overline X$ de $\R[x]_3$ tal que $X\subseteq \overline X$.

Exercício 64.11 Sejam $U,W$ subespaços de um espaço vetorial $V$. Demonstre que $U\cup W$ é um subespaço de $V$ se e somente se $U\subseteq W$ ou $W\subseteq U$. (Dica: veja a conversa na página de stackexchange.)

Solução:

($\Leftarrow$): Suponha sem perda de generalidade que $U \subseteq W$ . Então, $U \cup W = W$. Como $W$ é um subespaço de $V$, $U \cup W$ é um subespaço de ( V ). O caso $W \subseteq U$ é análogo.

($\Rightarrow$): Suponhamos que $U \cup W$ é um subespaço de $V$ e que tenhamos o caso $U \not\subseteq W$; afirmamos então que
$W \subseteq U$. De fato, por nossa suposição existe um vetor $u \in U \setminus W$. Agora, se $w$ é um vetor qualquer em $W$
temos que $u+w \in U \cup W$ pois um subespaço é fechado por soma. Daí note que $u+w$ não pode pertencer a $W$, pois se não $(u + w) + (-w) = u $ estaria em $W$ e isso iria contradizer nossa hipótese de que $ U W$. Logo a única opção é que $u+w$ esteja em $U$ e como $u$ já pertence a $U$ temos que $(u+w) +(-u) = w$ também
percente a $U$, logo como $w$ é arbitrário concluímos que $W \subseteq U$. Analogamente o leitor pode supor o caso em que $W \not\subseteq U$ e, utilizando o mesmo argumento, provar que $U\subseteq W$.

(Caio Monteiro)

Exercício 64.12 Seja $\F$ um corpo de caraterística diferente de 2 e seja $V=M_n(\F)$ (espaço de matrizes $n\times n$ sobre $\F$). Para $A\in V$, denotamos a transposta de $A$ com $A^t$. Defina \[\begin{align*} U_1&=\{A\in V\mid A^t=A\};\\ U_2&=\{A\in V\mid A^t=-A\}. \end{align*}\] Ou seja, $U_1$ é o conjunto das matrizes simétricas, enquanto $U_2$ é o conjunto das matrizes antisimétricas em $V$.

Mostre que $V=U_1\oplus U_2$.
Explique a necessidade da condição que a caraterística de $\F$ é diferente de 2. Dica: Consulte o 57.2

Exercício 64.13 Sejam $U_1,U_2,\ldots,U_k$ subespaçose de um espaço vetorial $V$. Mostre que as segunites afirmações são equivalentes:

Todo elemento $v\in V$ pode ser escrito unicamente como $v=u_1+\cdots+u_k$ com $u_i\in U_i$.
$V=U_1+\cdots+U_k$ e $U_i\cap (\sum_{j\neq i}U_j)=0$ para todo $i\in\{1,\ldots,k\}$.

Exercício 64.14 Decide quais dos seguintes conjuntos são subespaços de $V=\mbox{Func}([0,1],\R)$.

$\{f\in V\mid f\mbox{ é limitado}\}$;
$\{f\in V\mid f\mbox{ é limitado superiormente}\}$;
$\{f\in V\mid f\mbox{ é limitado inferiormente}\}$;
$\{f\in V\mid f\mbox{ é diferenciável}\}$;
$\{f\in V\mid f\mbox{ é contínua}\}$;
$\{f\in V\mid f\mbox{ é crescente}\}$;

Solução:

$\{f\in V\mid f\mbox{ é limitado}\}$ é um subespaço de $V$. A soma de funções limitadas é limitada, e o produto de uma função limitada por um escalar também é limitado.
$\{f\in V\mid f\mbox{ é limitado superiormente}\}$ não é um subespaço de $V$. Por exemplo se $f(0)=0$ e f(x)=x$ para $x\in (0,1)$ então, $f$ é limitado superiormente, mas $-f$ não é limitado superiormente.
$\{f\in V\mid f\mbox{ é limitado inferiormente}\}$ não é um subespaço de $V$. O mesmo argumento do item anterior se aplica.
$\{f\in V\mid f\mbox{ é diferenciável}\}$ é um subespaço de $V$. A soma de funções diferenciáveis é diferenciável, e o produto de uma função diferenciável por um escalar também é diferenciável.
$\{f\in V\mid f\mbox{ é contínua}\}$ é um subespaço de $V$. A soma de funções contínuas é contínua, e o produto de uma função contínua por um escalar também é contínua.
$\{f\in V\mid f\mbox{ é crescente}\}$ não é um subespaço de $V$, pois a função nula não é cresdente e não pertence ao subespaço.

Exercício 64.15 Defina os seguintes vetores em $\R^6$: \[\begin{align*} v_1 &=( 1, 1, -1, -1, 0, 0)\\ v_2 &= ( 1, 1, 0, 0, -1, 1)\\ v_3 &= (-1, -1, -1, -1, 0, 0)\\ v_4 &= ( 0, 0, -1, -1, 2, 0)\\ v_5 &= ( 0, 0, 0, 0, 1, 0)\\ v_6 &= ( 0, 0, 0, 0, -1, -1)\\ \end{align*}\] Defina $U_1=\left<v_1,v_2,v_3\right>$ e $U_2=\left<v_4,v_5,v_6\right>$.

Determine uma base para $U_1\cap U_2$.
Estenda a base determinada no primeiro ponto para uma base de $U_1$ e também para uma base de $U_2$.
Determina uma base de $U_1+U_2$.

Exercício 64.16 Ache um complemento para o espaço $U_1$ em $V$ no exercício anterior.

Exercício 64.17 Seja $\F$ um corpo com cardinalidade finita.

Deduza do Exercício 64.4 que a caraterística de $\F$ é um primo $p$.
Mostre que $\F$ é um espaço vetorial sobre o corpo $\Z_p$.
Deduza que $\dim \F$ (considerado como $\Z_p$-espaço) é finita e ponha $\dim \F=d$.
Mostre que $|\F|=p^d$.
Parabens! Você acabou de demonstrar o seguinte teorema: ``Se $\F$ é um corpo finito, então a cardinalidade de $\F$ é uma potência de um primo’’. (Dica: página no stackexchange)

Solução:

Se a característica de um corpo é $0$ poderíamos somar a unidade $1$ de $\mathbb{F}$ quantas vezes quisermos que sempre obteríamos elementos diferentes dentro do corpo, portanto um corpo de característica 0 só pode ser infinito. Por contrapositiva concluímos que um corpo finito deve possuir característica estritamente positiva e, pelo Exercício 64.4, característica prima, para algum primo $p$. No entanto, se a característica for diferente de zero isso não significa que o corpo tenha que ser finito, procure um exemplo em que isso aconteça.
Como $\mathbb{F}$ é um corpo ele já é fechado por soma e satisfaz a comutatividade da adição de vetores, associatividade da adição de vetores, existência de vetor nulo (o $0$ de $\mathbb{F}$) e de inverso aditivo, uma vez que o inverso do vetor $v$ em $\mathbb{F}$ é o negativo de $v$ como elemento do corpo, isto é , $-v$. Resta verificar a multiplicação por escalar, que pode ser assim definida. Para cada $\alpha$ em $\mathbb{Z}_{p} =\{\overline{0},\overline{1}, ..., \overline{p-1} \}$ e $v \in \mathbb{F}$ defina $\alpha \cdot v$ como somar o vetor $v$ em $\mathbb{F}$ uma quantidade $\alpha$ de vezes ($\alpha$ visto como um número natural). Ao utilizarmos a aritmética módulo $p$ e o fato de que $\mathbb{F}$ tem característica $p$, isto é, somar um vetor qualquer de $\mathbb{F}$ $p$ vezes sempre retorna $0$, podemos verificar que essa multiplicação por escalar satisfaz os demais axiomas de espaço vetorial. Mais que isso, ao somarmos o elemento $1$ de $\mathbb{F}$ um número $p$ de vezes poderemos ver que temos uma cópia de $\mathbb{Z}_{p}$ contido em $\mathbb{F}$ e que neste contexto é geralmente chamado subcorpo primo de $\mathbb{F}$.
Como mostrado no item $2$ temos que $\mathbb{F}$ é espaço vetorial sobre $\mathbb{Z}_{p}$ e portanto possui uma base, que é um subconjunto de $\mathbb{F}$ e como esse último é finito segue que a cardinalidade da base também é finita. Vamos denotar por $d$ a dimensão de $\mathbb{F}$ visto como $\mathbb{Z}_{p}$ - espaço vetorial.
Como todo elemento de $\mathbb{F}$ pode ser escrito unicamente como combinação linear de elementos de uma base com cardinalidade $d$ existe pelo Princípio fundamental da contagem $p$ elevado a $d$ combinações lineares distintas possíveis para elementos de $\mathbb{F}$ e portanto $|\mathbb{F}| = p^d$.

(Caio Monteiro)

Exercício 64.18 Se $B$ é o sistema $b_1,\ldots,b_k$ de vetores de $\F^n$, denote por $M_B$ a matriz $k\times n$ cujas linhas são $b_1,\ldots,b_k$.

Seja $V\leq \F^n$. Mostre que $V$ possui uma base $B$ tal que $M_B$ está na forma escalonada reduzida.
Mostre que a base $B$ no item anterior é única para o espaço $V$.

Exercício 64.19 Escreva uma função em uma linguagem de programação (por exemplo, Python) que toma duas matrizes (arrays) $A$ e $B$ com entradas no mesmo corpo e devolva True se os espaços gerados pelas linhas de $A$ e $B$ (respectivamente) são iguais. A função deve devolver False no caso contrário.

Dica:

Use o exercício anterior e ache as formas escalonadas reduzidas de $A$ e $B$ usando alguma implementação da Eliminação de Gauss-Jordan. Se usar Python, pode usar a função rref na biblioteca SymPy.

Exercício 64.20 Seja $V\leq\F^n$ e assuma que $B=\{b_1,\ldots,b_k\}$ é base de $V$ tal que $M_B$ está na forma escalonada reduzida. Assuma que o pivô da linha $i$ está na coluna $p_i$. Seja $v=(v_1,\ldots,v_n)\in \F^n$ arbitrário e defina \[ v_B=v-\sum_{i=1}^kv_{p_i}b_i. \]

Mostre que $v+V=v_B+V$.
Mostre que $(v_B)_{p_i}=0$ para todo $i$.
Mostre, para $v,w\in\F^n$, que $v+V=w+V$ se e somente se $v_B=w_B$.

Exercício 64.21 O exercício anterior pode ser usado para decidir igualdade da forma algorítmica no quociente $\F^n/V$. Escreva uma função em uma linguagem de programação (por exemplo, Python) que toma uma matriz $B$ $(k\times n)$ na forma escalonada reduzida e toma dois vetores $v,w\in\F^n$ e devolve True se e somente se $v+V=w+V$, onde $V$ denota o espaço gerado pelas linhas de $B$.

Dica:

Implemente o procedimento no exercício anterior e verifique se $v_B=w_B$.

Exercício 64.22 Sejam $V$ e $W$ $\F$-espaços vetoriais de dimensão finita com $\dim V=k$ e $\dim W=m$. Assuma que $B=\{b_1,\ldots,b_k\}$ e $C=\{c_1,\ldots,c_m\}$ são bases de $V$ e $W$, respectivamente.

Considere o mapa \[ \psi:\mbox{Hom}(V,W)\to W^{k\oplus},\quad f\mapsto (f(b_1),\ldots,f(b_k)) \] onde $W^{k\oplus}=W\oplus\cdots\oplus W$ (soma direta externa de $k$ cópias de $W$). Mostre que $\psi$ é um isomorfismo.
Mostre que $f\mapsto [f]_C^B$ é um isomorfismo $\mbox{Hom}(V,W)\to M_{m\times k}(\F)$.

Solução:

Para mostrar que $\psi$ é um isomorfismo, precisamos verificar que $\psi$ é linear, injetiva e sobrejetiva.
- Linearidade: Seja $f, g \in \mbox{Hom}(V, W)$ e $\alpha \in \F$. Então: \[ \psi(\alpha f + g) = ((\alpha f + g)(b_1), \ldots, (\alpha f + g)(b_k)). \] Pela definição de $\alpha f+g$, isso se torna: \[ \psi(\alpha f + g) = (\alpha f(b_1) + g(b_1), \ldots, \alpha f(b_k) + g(b_k)). \] Por outro lado: \[ \alpha \psi(f) + \psi(g) = \alpha (f(b_1), \ldots, f(b_k)) + (g(b_1), \ldots, g(b_k)). \] Isso é igual a: \[ (\alpha f(b_1) + g(b_1), \ldots, \alpha f(b_k) + g(b_k)). \] Portanto, $\psi(\alpha f + g) = \alpha \psi(f) + \psi(g)$, mostrando que $\psi$ é linear.
- Injetividade: Para verificar que $\psi$ é injetiva, verificamos que $\ker \psi = \{0\}$. Suponha que $f \in \ker \psi$. Isso significa que: \[ \psi(f) = (f(b_1), \ldots, f(b_k)) = (0, \ldots, 0). \] Portanto, $f(b_i) = 0$ para todo $i = 1, \ldots, k$. Como $B$ é uma base de $V$, qualquer vetor em $V$ pode ser escrito como uma combinação linear dos vetores de $B$. Assim, $f(v) = 0$ para todo $v \in V$, o que implica que $f$ é a transformação nula. Concluímos que $\ker \psi = \{0\}$, mostrando que $\psi$ é injetiva.
- Sobrejetividade: Seja $(w_1, \ldots, w_k) \in W^{k\oplus}$. Defina $f \in \mbox{Hom}(V, W)$ por $f(b_i) = w_i$ para $i = 1, \ldots, k$ e estenda linearmente. Então $\psi(f) = (w_1, \ldots, w_k)$. Portanto, $\psi$ é sobrejetiva.
Concluímos que $\psi$ é um isomorfismo.

Exercício 64.23 Seja $V=\F_3[x]_3$ e considere as bases $B=\{1,x,x^2,x^3\}$ e $C=\{1,1-x,1-x^2,1-x^3\}$. Seja $d:V\to V$ o endomorfismo definido com $d(f)=f'$ (derivado formal).

Ache as matrizes $[\mbox{id}_V]_B^C$ e $[\mbox{id}_V]_C^B$.
Ache as matrizes $[f]_B^B$, $[f]_B^C$, $[f]_C^B$ e $[f]_C^C$.

Exercício 64.24 Sejam $V$ e $W$ espaços vetoriais de dimensão finita sobre $\F$ com bases $B$ e $C$, respetivamente. Denote por $B^∗$ e $C^∗$ as bases duais de $B$ e $C$ em $V^∗$ e $W^∗$, respetivamente. Seja $f : V \to W$ linear e considere o dual $f^∗ : W^∗ \to V^∗$. Mostre que \[ [f^∗]^{C^∗}_{B^*} = ([f]^B_C)^t. \] Dica:

Solução:

Sejam $V$ e $W$ espaços vetoriais de dimensão finita sobre $\F$ com bases $B$ e $C$, respectivamente. Denote por $B^∗$ e $C^∗$ as bases duais de $B$ e $C$ em $V^∗$ e $W^∗$, respectivamente. Seja $f : V \to W$ linear e considere o dual $f^∗ : W^∗ \to V^∗$. Vamos mostrar que \[ [f^∗]^{C^∗}_{B^*} = ([f]^B_C)^t. \]

Definição do dual:
- O dual $f^∗ : W^∗ \to V^∗$ é definido por $f^∗(\varphi) = \varphi \circ f$ para todo $\varphi \in W^∗$.
- Isso significa que $f^∗$ “puxa para trás” os funcionais lineares de $W^∗$ para $V^∗$.
Representação matricial:
- Seja $[f]^B_C$ a matriz que representa $f$ em relação às bases $B$ e $C$.
- Seja $[f^∗]^{C^∗}_{B^*}$ a matriz que representa $f^∗$ em relação às bases duais $C^∗$ e $B^∗$.
Propriedade das bases duais:
- Por definição, as bases duais $B^∗ = \{\beta_1^∗, \ldots, \beta_n^∗\}$ e $C^∗ = \{\gamma_1^∗, \ldots, \gamma_m^∗\}$ satisfazem: \[ \beta_i^∗(b_j) = \delta_{ij}, \quad \gamma_i^∗(c_j) = \delta_{ij}, \] onde $\delta_{ij}$ é o delta de Kronecker.
Cálculo de $[f^∗]^{C^∗}_{B^*}$:
- Para calcular $[f^∗]^{C^∗}_{B^*}$, precisamos determinar as coordenadas de $f^∗(\gamma_j^∗)$ em relação à base $B^∗$.
- Por definição de $f^∗$, temos: \[ f^∗(\gamma_j^∗)(b_i) = \gamma_j^∗(f(b_i)). \]
- Isso significa que a entrada $(i, j)$ de $[f^∗]^{C^∗}_{B^*}$ é dada por $\gamma_j^∗(f(b_i))$.
Relação com $[f]^B_C$:
- A matriz $[f]^B_C$ é definida por $f(b_i) = \sum_{j=1}^m a_{ji} c_j$, onde $a_{ji}$ são as entradas de $[f]^B_C$.
- Portanto, $\gamma_j^∗(f(b_i)) = a_{ji}$.
Conclusão:
- As entradas de $[f^∗]^{C^∗}_{B^*}$ são dadas por $a_{ji}$, que são as entradas transpostas de $[f]^B_C$.
- Assim, temos: \[ [f^∗]^{C^∗}_{B^*} = ([f]^B_C)^t. \]

Exercício 64.25 Seja $V$ um espaço vetorial e $U \leq V$. Deﬁna \[ U^0 =\{\varphi\in V^∗ \mid \varphi(u)=0\mbox{ para todo }u\in U\}. \]

Demonstre que $U^0 \leq V^*$.
Mostre que $\dim U + \dim U^0 = \dim V$ no caso quando $\dim V$ é finita.

Seja $f : V \to W$ uma aplicação linear e considere o dual $f^∗ : W^∗ \to V^∗$.

Mostre que $\ker f^∗ = (\mbox{Im}\,f)^0$.
Mostre que $\mbox{Im}\,f^∗ = (\ker f)^0$.

Solução:

Demonstre que $U^0 \leq V^*$:
- Para mostrar que $U^0$ é um subespaço de $V^*$, verificamos as condições de fechamento para soma e multiplicação escalar:
  - Seja $\varphi_1, \varphi_2 \in U^0$. Então, para todo $u \in U$, temos: \[ (\varphi_1 + \varphi_2)(u) = \varphi_1(u) + \varphi_2(u) = 0 + 0 = 0. \] Logo, $\varphi_1 + \varphi_2 \in U^0$.
  - Seja $\varphi \in U^0$ e $\alpha \in \F$. Então, para todo $u \in U$, temos: \[ (\alpha \varphi)(u) = \alpha \varphi(u) = \alpha \cdot 0 = 0. \] Logo, $\alpha \varphi \in U^0$.
  - Assim, $U^0$ é fechado para soma e multiplicação escalar, e portanto $U^0 \leq V^*$.
Mostre que $\dim U + \dim U^0 = \dim V$ no caso quando $\dim V$ é finita:
- Seja $B = \{b_1, \ldots, b_k\}$ uma base de $U$ e complete $B$ para uma base $B' = \{b_1, \ldots, b_k, b_{k+1}, \ldots, b_n\}$ de $V$.
- Considere a base dual $B^* = \{b_1^*, \ldots, b_n^*\}$ de $V^*$.
- Note que $U^0 = \langle b_{k+1}^*, \ldots, b_n^* \rangle$, pois os funcionais $b_{k+1}^*, \ldots, b_n^*$ anulam todos os vetores de $U$, mas se $\varphi=\sum_{i}\alpha_ib_i^*$ é um funcional com $\alpha_i\neq 0$ com $i\in\{1,\ldots,k\}$ então $\varphi(b_k)=\alpha_i\neq 0$.
- Assim, $\dim U^0 = n - k$ e $\dim U = k$. Como $\dim V = n$, temos: \[ \dim U + \dim U^0 = k + (n - k) = n = \dim V. \]
Mostre que $\ker f^∗ = (\mbox{Im}\,f)^0$:
- Por definição, $\ker f^* = \{\varphi \in W^* \mid f^*(\varphi) = 0\}$.
- Para $\varphi \in W^*$, temos $f^*(\varphi)(v) = \varphi(f(v))$ para todo $v \in V$.
- Assim, $f^*(\varphi) = 0$ significa que $\varphi(f(v)) = 0$ para todo $v \in V$, ou seja, $\varphi$ anula todos os vetores de $\mbox{Im}\,f$.
- Portanto, $\ker f^* = (\mbox{Im}\,f)^0$.
Mostre que $\mbox{Im}\,f^∗ = (\ker f)^0$:
- Por definição, $\mbox{Im}\,f^* = \{f^*(\varphi) \mid \varphi \in W^*\}$.
- Para $\psi \in V^*$, temos $\psi \in \mbox{Im}\,f^*$ se e somente se existe $\varphi \in W^*$ tal que $\psi(v) = \varphi(f(v))$ para todo $v \in V$.
- Isso significa que $\psi$ anula todos os vetores de $\ker f$, pois se $v \in \ker f$, então $f(v) = 0$ e $\psi(v) = \varphi(0) = 0$.
- Assim, $\mbox{Im}\,f^* \subseteq (\ker f)^0$.
- Por outro lado, se $\psi \in (\ker f)^0$, então $\psi$ anula todos os vetores de $\ker f$, e podemos definimos $\varphi \in W^*$ na seguinte forma. Seja $Z$ um complemento de $\mbox{Im}(f)$ em $W$; ou seja $W=\mbox{Im}(f)\oplus Z$. Defina $\varphi$ em $\mbox{Im}(f)$ tal que $\psi(v) = \varphi(f(v))$ para todo $v \in V$ e defina $\vaphi$ em $Z$ tal que $\varphi(z)=0$ para todo $z\in Z$. Note que $\varphi$ está bem definida e $\psi=f^*(\varphi)$.
- Portanto, $\mbox{Im}\,f^* = (\ker f)^0$.

Exercício 64.26 Deduza do exercício anterior que $f$ é injetiva se e somente se $f^∗$ é sobresetiva e que $f$ é sobrejetiva se e somente se $f^∗$ é injetiva.

Solução:

Deduza que $f$ é injetiva se e somente se $f^∗$ é sobrejetiva:
- Se $f$ é injetiva, então $\ker f = \{0\}$. Pelo exercício anterior, temos $\mbox{Im}\,f^∗ = (\ker f)^0$. Como $\ker f = \{0\}$, segue que $(\ker f)^0 = V^∗$. Portanto, $\mbox{Im}\,f^∗ = V^∗$, o que implica que $f^∗$ é sobrejetiva.
- Reciprocamente, se $f^∗$ é sobrejetiva, então $\mbox{Im}\,f^∗ = V^∗$. Pelo exercício anterior, $\mbox{Im}\,f^∗ = (\ker f)^0$. Como $(\ker f)^0 = V^∗$, segue que $\ker f = \{0\}$. Portanto, $f$ é injetiva.
Deduza que $f$ é sobrejetiva se e somente se $f^∗$ é injetiva:
- Se $f$ é sobrejetiva, então $\mbox{Im}\,f = W$. Pelo exercício anterior, $\ker f^∗ = (\mbox{Im}\,f)^0$. Como $\mbox{Im}\,f = W$, segue que $(\mbox{Im}\,f)^0 = \{0\}$. Portanto, $\ker f^∗ = \{0\}$, o que implica que $f^∗$ é injetiva.
- Reciprocamente, se $f^∗$ é injetiva, então $\ker f^∗ = \{0\}$. Pelo exercício anterior, $\ker f^∗ = (\mbox{Im}\,f)^0$. Como $(\mbox{Im}\,f)^0 = \{0\}$, segue que $\mbox{Im}\,f = W$. Portanto, $f$ é sobrejetiva.

Exercício 64.27 [Segundo Teorema de Isomorﬁsmo] Seja $V$ um espaço vetorial e $U,W \leq V$. Mostre, exibindo um isomorﬁsmo, que \[ (U +W)/W \cong U/(U \cap W). \]

Solução:

Para demonstrar o Segundo Teorema de Isomorfismo, considere a aplicação \[ \phi: U \to (U + W)/W, \quad u \mapsto u + W. \] Essa aplicação é bem definida, pois para qualquer $u \in U$, o coset $u + W$ pertence ao quociente $(U + W)/W$.

Agora, verificamos que $\phi$ é linear. Para $u_1, u_2 \in U$ e $\alpha \in \F$, temos: \[ \phi(\alpha u_1 + u_2) = (\alpha u_1 + u_2) + W = \alpha(u_1 + W) + (u_2 + W) = \alpha \phi(u_1) + \phi(u_2). \] Portanto, $\phi$ é uma transformação linear.

Mostremos que $\phi$ é sobrejetiva. Seja $v + W \in (U + W)/W$ um elemento arbitrário do quociente. Como $v \in U + W$, podemos escrever $v = u + w$ para algum $u \in U$ e $w \in W$. Assim: \[ v + W = (u + w) + W = u + W, \] onde usamos o fato de que $w \in W$ implica $w + W = W$. Portanto, $v + W$ é a imagem de $u \in U$ sob $\phi$, o que mostra que $\phi$ é sobrejetiva.

O núcleo de $\phi$ é dado por: \[ \ker \phi = \{u \in U \mid \phi(u) = W\} = \{u \in U \mid u + W = W\}. \] Isso significa que $u \in \ker \phi$ se e somente se $u \in W$. Logo: \[ \ker \phi = U \cap W. \]

Pelo Primeiro Teorema de Isomorfismo, temos: \[ U / \ker \phi \cong \mbox{Im}(\phi). \] Como $\phi$ é sobrejetiva, $\mbox{Im}(\phi) = (U + W)/W$. Assim, obtemos: \[ U / (U \cap W) \cong (U + W)/W. \] Portanto, $(U + W)/W \cong U / (U \cap W)$.

Exercício 64.28 [Terceiro Teorema de Isomorﬁsmo] Seja $V$ um espaço vetorial e $U,W \leq V$ tais que $W \leq U$. Mostre que \[ (V/W)/(U/W)\cong V/U. \]

Solução:

Para demonstrar o Terceiro Teorema de Isomorfismo, considere a aplicação \[ \phi: V/W \to (V/W)/(U/W), \quad v + W \mapsto (v + W) + (U/W). \] Essa aplicação é bem definida, pois para qualquer $v \in V$, o coset $(v + W) + (U/W)$ pertence ao quociente $(V/W)/(U/W)$.

Agora, verificamos que $\phi$ é linear. Para $v_1, v_2 \in V$ e $\alpha \in \F$, temos: \[ \phi(\alpha (v_1 + W) + (v_2 + W)) = \phi((\alpha v_1 + v_2) + W) = ((\alpha v_1 + v_2) + W) + (U/W). \] Por outro lado: \[ \alpha \phi(v_1 + W) + \phi(v_2 + W) = \alpha ((v_1 + W) + (U/W)) + ((v_2 + W) + (U/W)). \] Ambas as expressões são iguais, mostrando que $\phi$ é linear.

Mostremos que $\phi$ é sobrejetiva. Seja $(v + W) + (U/W) \in (V/W)/(U/W)$ um elemento arbitrário do quociente. Por definição, $(v + W) + (U/W)$ é a imagem de $v + W \in V/W$ sob $\phi$. Portanto, $\phi$ é sobrejetiva.

O núcleo de $\phi$ é dado por: \[ \ker \phi = \{v + W \in V/W \mid \phi(v + W) = U/W\}. \] Isso significa que $v + W \in \ker \phi$ se e somente se $(v + W) + (U/W) = U/W$, ou seja, $v + W \in U/W$. Logo: \[ \ker \phi = U/W. \]

Pelo Primeiro Teorema de Isomorfismo, temos: \[ (V/W)/\ker \phi \cong \mbox{Im}(\phi). \] Como $\ker \phi = U/W$, obtemos: \[ (V/W)/(U/W) \cong V/U. \] Portanto, $(V/W)/(U/W) \cong V/U$.

Exercício 64.29 Deduza do Segundo Teorema de Isomorﬁsmo a fórmula para a dimensão de $U +W$.

Solução:

A fórmula para a dimensão de $U + W$ pode ser deduzida do Segundo Teorema de Isomorfismo. Pelo teorema, temos: \[ (U + W)/W \cong U/(U \cap W). \]

Tomando as dimensões de ambos os lados, obtemos: \[ \dim((U + W)/W) = \dim(U/(U \cap W)). \]

Sabemos que, para um quociente de espaços vetoriais, a dimensão é dada por: \[ \dim((U + W)/W) = \dim(U + W) - \dim(W), \] e \[ \dim(U/(U \cap W)) = \dim(U) - \dim(U \cap W). \]

Igualando as duas expressões, obtemos: \[ \dim(U + W) - \dim(W) = \dim(U) - \dim(U \cap W). \]

Rearranjando, temos: \[ \dim(U + W) = \dim(U) + \dim(W) - \dim(U \cap W). \]

Portanto, a fórmula para a dimensão de $U + W$ é: \[ \dim(U + W) = \dim(U) + \dim(W) - \dim(U \cap W). \]

Exercício 64.30 Seja $W$ um espaço vetorial sobre $\F$. Deﬁne o functor $H_W$ com as seguintes regras:

Para um $\F$-espaço vetorial $V$, defina $H_W(V) = \mbox{Hom}(W,V)$.
Para uma transformação linear $f : V \to U$, defina \[ H_W (f):\mbox{Hom}(W,V)\to \mbox{Hom}(W,U),\quad H_W (f)(α)=f\circ α. \]

Demonstre as seguintes afirmações.

Demonstre, para todo $\F$-espaço $V$, que $H_W(\mbox{id}_V) = \mbox{id}_{\textrm{Hom}(W,V)}$.
Demonstre que se $f : V_1 \to V_2$ e $g : V_2 \to V_3$ são transformações lineares, então $H_W(g\circ f) = H_W(g)\circ H_W(f)$.

As propriedades mostram que o functor $H_W$ é um functor covariante na categoria dos $\F$-espaços vetoriais.

Solução:

Para todo $\F$-espaço $V$, temos que $H_W(\mbox{id}_V)$ é a aplicação: \[ H_W(\mbox{id}_V)(\alpha) = \mbox{id}_V \circ \alpha = \alpha, \quad \forall \alpha \in \mbox{Hom}(W, V). \] Isso mostra que $H_W(\mbox{id}_V) = \mbox{id}_{\textrm{Hom}(W,V)}$.
Para $f : V_1 \to V_2$ e $g : V_2 \to V_3$, temos que $H_W(g \circ f)$ é a aplicação: \[ H_W(g \circ f)(\alpha) = (g \circ f) \circ \alpha = g \circ (f \circ \alpha), \quad \forall \alpha \in \mbox{Hom}(W, V_1). \] Por outro lado, $H_W(g) \circ H_W(f)$ é a aplicação: \[ (H_W(g) \circ H_W(f))(\alpha) = H_W(g)(H_W(f)(\alpha)) = H_W(g)(f \circ \alpha) = g \circ (f \circ \alpha). \] Assim, $H_W(g \circ f) = H_W(g) \circ H_W(f)$.

Portanto, o functor $H_W$ é covariante.

Exercício 64.31 Seja $W$ como no Exercício 64.30. Mostre que se $f : V \to U$ é injetiva/sobrejetiva, então \[ H_W(f):\mbox{Hom}(W,V)\to\mbox{Hom}(W,U) \] é injetiva/sobrejetiva (respetivamente).

Solução:

Injetividade: Suponha que $f : V \to U$ é injetiva. Seja $\alpha \in \mbox{Hom}(W, V)$ tal que $H_W(f)(\alpha) = f \circ \alpha = 0$. Isso implica que $f(\alpha(w)) = 0$ para todo $w \in W$. Como $f$ é injetiva, segue que $\alpha(w) = 0$ para todo $w \in W$, ou seja, $\alpha = 0$. Portanto, $H_W(f)$ é injetiva.
Sobrejetividade: Suponha que $f : V \to U$ é sobrejetiva. Seja $\beta \in \mbox{Hom}(W, U)$. Como $f$ é sobrejetiva, para cada $w \in W$, existe $v \in V$ tal que $f(v) = \beta(w)$. Defina $\alpha \in \mbox{Hom}(W, V)$ por $\alpha(w) = v$. Então, $H_W(f)(\alpha) = f \circ \alpha = \beta$. Assim, $H_W(f)$ é sobrejetiva.

Exercício 64.32 O functor $H_W$ está frequentamente escrito como $\mbox{Hom}(W,−)$ e escrevemos também $H_W(V) = \mbox{Hom}(W,V)$ e $H_W(f) = \mbox{Hom}(W,f)$. Deﬁna um functor $\mbox{Hom}(−,W)$. Este outro functor seria um functor covariante ou contravariante?

Exercício 64.33 Seja $\F[[x]]$ o espaço das séries de potências sobre um corpo $\F$; ou seja, \[ \F[[x]]=\left\{\sum_{k\geq 0}\alpha_ix^i\mid \alpha_i\in\F\right\}; \] Demonstre que $\F[x]^*\cong \F[[x]]$.

Solução:

Para demonstrar que $\F[x]^* \cong \F[[x]]$, construiremos um isomorfismo explícito entre os dois espaços.

Definição de $\F[x]^*$:
- O espaço $\F[x]^*$ é o dual de $\F[x]$, ou seja, o espaço de todos os funcionais lineares $\varphi: \F[x] \to \F$.
Definição de $\F[[x]]$:
- O espaço $\F[[x]]$ consiste em todas as séries formais de potências $\sum_{k \geq 0} \alpha_k x^k$, onde $\alpha_k \in \F$.
Construção do isomorfismo:
- Para cada série formal $f(x) = \sum_{k \geq 0} \alpha_k x^k \in \F[[x]]$, definimos um funcional linear $\varphi_f \in \F[x]^*$ como: \[ \varphi_f(x^i) = \alpha_i, \quad \forall i \geq 0. \] Em outras palavras, $\varphi_f$ é o funcional linear que mapeia cada monômio $x^i$ ao coeficiente $\alpha_i$ da série formal $f(x)$. Como os $x^i$ formam uma base para $\F[x]$, este mapeamento pode ser estendido de forma única para um elemento de $\F[x]^*$.
Injetividade:
- Para mostrar que o mapeamento é injetivo, considere o núcleo do mapeamento. Seja $\varphi_f \in \F[x]^*$ tal que $\varphi_f(x^i) = 0$ para todo $i \geq 0$. Isso implica que todos os coeficientes $\alpha_i$ da série formal $f(x) = \sum_{k \geq 0} \alpha_k x^k$ são zero. Portanto, $f(x) = 0$, o que mostra que o núcleo contém apenas o elemento nulo. Assim, o mapeamento é injetivo.
Sobrejetividade:
- Seja $\varphi \in \F[x]^*$. Definimos uma série formal $f(x) = \sum_{k \geq 0} \alpha_k x^k$, onde $\alpha_k = \varphi(x^k)$. É claro pela definição de de $\varphi_f$ que $\varphi_f=\varphi$.
Conclusão:
- O mapeamento $f(x) \mapsto \varphi_f$ é um isomorfismo linear entre $\F[[x]]$ e $\F[x]^*$. Assim, $\F[x]^* \cong \F[[x]]$.

Exercício 64.34 Sejam $V$ e $W$ $\F$-espaços vetoriais, sejam $\Psi_V:V\to V^{**}$ e $\Psi_W:W\to W^{**}$ as funções canônicas definidas no Lema 61.2, e seja $f:V\to W$ uma transformação linear. Mostre que o seguinte diagrama comuta.

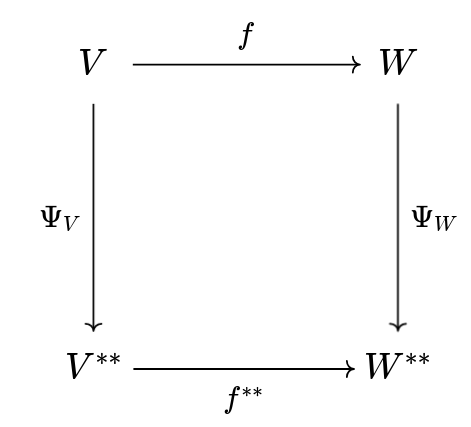
Dica: Consulte esta e esta conversa no Stackexhange.

Este exercícios mostra que a transformação $\Psi_V$ é uma transformação natural entre o functor da identidade e o functor bidual $(-)^{**}$ na categoria dos $\F$-espaços vetoriais.

Solução:

Para mostrar que o diagrama comuta, precisamos verificar que $\Psi_W \circ f = f^{**} \circ \Psi_V$, onde $f^{**}: V^{**} \to W^{**}$ é o mapa dual-dual de $f$.

Definição de $\Psi_V$ e $\Psi_W$:
- Para cada $v \in V$, $\Psi_V(v)$ é o funcional em $V^{**}$ definido por: \[ \Psi_V(v)(\varphi) = \varphi(v), \quad \forall \varphi \in V^*. \]
- Analogamente, para cada $w \in W$, $\Psi_W(w)$ é o funcional em $W^{**}$ definido por: \[ \Psi_W(w)(\psi) = \psi(w), \quad \forall \psi \in W^*. \]
Definição de $f^{**}$:
- Para cada $\Phi \in V^{**}$, $f^{**}(\Phi)$ é o funcional em $W^*$ definido por: \[ f^{**}(\Phi)(\psi) = \Phi(f^*(\psi)), \quad \forall \psi \in W^*, \] onde $f^*: W^* \to V^*$ é o mapa dual de $f$, dado por $f^*(\psi)(v) = \psi(f(v))$.
Verificação da comutatividade:
- Seja $v \in V$. Precisamos mostrar que: \[ (\Psi_W \circ f)(v) = (f^{**} \circ \Psi_V)(v). \]
- Calculando $(\Psi_W \circ f)(v)$: \[ (\Psi_W \circ f)(v) = \Psi_W(f(v)). \] Para $\psi \in W^*$, temos: \[ \Psi_W(f(v))(\psi) = \psi(f(v)). \]
- Calculando $(f^{**} \circ \Psi_V)(v)$: \[ (f^{**} \circ \Psi_V)(v) = f^{**}(\Psi_V(v)). \] Para $\psi \in W^*$, temos: \[ f^{**}(\Psi_V(v))(\psi) = \Psi_V(v)(f^*(\psi)). \] Por definição de $\Psi_V$, temos: \[ \Psi_V(v)(f^*(\psi)) = f^*(\psi)(v). \] Por definição de $f^*$, temos: \[ f^*(\psi)(v) = \psi(f(v)). \]
- Concluímos que: \[ (\Psi_W \circ f)(v)(\psi) = (f^{**} \circ \Psi_V)(v)(\psi), \] para todo $\psi \in W^*$. Portanto, $(\Psi_W \circ f)(v) = (f^{**} \circ \Psi_V)(v)$.
Conclusão:
- O diagrama comuta, ou seja, $\Psi_W \circ f = f^{**} \circ \Psi_V$.

Exercício 64.35 Demonstre Teorema 56.1, Lema 58.1, e resolva Exercício 57.1, Exercício 59.1, Exercício 59.2, Exercício 59.3, Exercício 60.1, Exercício 60.2, Exercício 61.1.

Exercício 64.36 Sejam $U$ e $V$ espaços vetoriais sobre $\F$. Mostre que a aplicação $u\otimes v\mapsto v\otimes u$ ($u\in U$ e $v\in V$) pode ser estendida unicamente para um isomorfismo bem definido $U\otimes V\to V\otimes U$.

Solução:

Definição do mapa bilinear:
- Seja $u \in U$ e $v \in V$. Definimos a aplicação bilinear $f: U \times V \to V \otimes U$ por: \[ f(u, v) = v \otimes u. \]
- Verificamos que $f$ é bilinear:
  - Para $u_1, u_2 \in U$, $v_1, v_2 \in V$, e $\alpha, \beta \in \F$, temos: \[ f(\alpha u_1 + \beta u_2, v) = v \otimes (\alpha u_1 + \beta u_2) = \alpha (v \otimes u_1) + \beta (v \otimes u_2), \] o que mostra a linearidade em $U$.
  - Similarmente, para combinações lineares em $V$, temos: \[ f(u, \alpha v_1 + \beta v_2) = (\alpha v_1 + \beta v_2) \otimes u = \alpha (v_1 \otimes u) + \beta (v_2 \otimes u), \] o que mostra a linearidade em $V$.
Extensão pelo produto tensorial:
- Pela propriedade universal do produto tensorial, existe uma única aplicação linear $T: U \otimes V \to V \otimes U$ tal que: \[ T(u \otimes v) = f(u, v) = v \otimes u. \]
- Assim, $T$ é a extensão linear de $f$ para todo $U \otimes V$.
Verificação de isomorfismo:
- Para verificar que $T$ é um isomorfismo, definimos $T^{-1}: V \otimes U \to U \otimes V$ por: \[ T^{-1}(v \otimes u) = u \otimes v. \]
- É fácil verificar que $T \circ T^{-1}$ e $T^{-1} \circ T$ são a identidade, mostrando que $T$ é um isomorfismo.

Portanto, $T$ é um isomorfismo bem definido entre $U \otimes V$ e $V \otimes U$.

Exercício 64.37 Seja $V$ um espaço vetorial de dimensão dois sobre um corpo $\F$ com base $b_1,b_2$. Mostre que não existem $u,v\in V$ tais que \[ b_1\otimes b_1+b_2\otimes b_2=u\otimes v. \]

Solução:

Para mostrar que não existem $u, v \in V$ tais que $b_1 \otimes b_1 + b_2 \otimes b_2 = u \otimes v$, usaremos o fato de que o produto tensorial é bilinear e que a decomposição de um tensor em um único produto tensorial é única.

Forma geral de $u \otimes v$:
- Seja $u = \alpha_1 b_1 + \alpha_2 b_2$ e $v = \beta_1 b_1 + \beta_2 b_2$, onde $\alpha_1, \alpha_2, \beta_1, \beta_2 \in \F$.
- Então: \[ u \otimes v = (\alpha_1 b_1 + \alpha_2 b_2) \otimes (\beta_1 b_1 + \beta_2 b_2). \]
- Expandindo usando a bilinearidade do produto tensorial: \[ u \otimes v = \alpha_1 \beta_1 (b_1 \otimes b_1) + \alpha_1 \beta_2 (b_1 \otimes b_2) + \alpha_2 \beta_1 (b_2 \otimes b_1) + \alpha_2 \beta_2 (b_2 \otimes b_2). \]
Comparação com $b_1 \otimes b_1 + b_2 \otimes b_2$:
- O tensor $b_1 \otimes b_1 + b_2 \otimes b_2$ não possui termos mistos como $b_1 \otimes b_2$ ou $b_2 \otimes b_1$.
- Para que $u \otimes v = b_1 \otimes b_1 + b_2 \otimes b_2$, os coeficientes de $b_1 \otimes b_2$ e $b_2 \otimes b_1$ devem ser zero. Isso implica: \[ \alpha_1 \beta_2 = 0 \quad \text{e} \quad \alpha_2 \beta_1 = 0. \]
Impossibilidade de satisfazer as condições:
- Se $\alpha_1 \beta_2 = 0$ e $\alpha_2 \beta_1 = 0$, então ou $\alpha_1 = 0$ ou $\beta_2 = 0$, e ou $\alpha_2 = 0$ ou $\beta_1 = 0$. É fácil verificar que nenhuma destas opções resulta no elemento $b_1\otimes b_1+b_2\otimes b_2$.
Conclusão:
- Não existem $u, v \in V$ tais que $b_1 \otimes b_1 + b_2 \otimes b_2 = u \otimes v$.

Exercício 64.38 Sejam $U$, $V$ e $W$ espaços vetoriais sobre $\F$. Mostre que a aplicação $(u\otimes v)\otimes w\mapsto u\otimes (v\otimes w)$ ($u\in U$, $v\in V$ e $w\in W$) pode ser estendida unicamente para um isomorfismo bem definido $(U\otimes V)\otimes W\to U\otimes (V\otimes W)$.

Dica:

Consulte a discussão no StackExchange.

Exercício 64.39 Sejam $U$ e $V$ espaços vetoriais sobre $\F$.

Mostre que a correspondência
\[ \varphi\otimes v\mapsto (u\mapsto \varphi(u)v) \] pode ser estendida a uma aplicação linear bem definida $\psi:U^*\otimes V\to \mbox{Hom}(U,V)$.
Mostre que quando $U$ e $V$ têm dimensão finita, então $\psi$ é um isomorfismo.

Solution:

Definição da aplicação linear $\psi$:
- Para cada $\varphi \in U^*$ e $v \in V$, definimos a aplicação bilinear $\psi: U^* \otimes V \to \mbox{Hom}(U, V)$ por: \[ \psi(\varphi, v)(u) = \varphi(u)v, \quad \forall u \in U. \]
- Verificamos que $\psi$ é bem definida e bilinear:
  - Para $\varphi_1, \varphi_2 \in U^*$, $v_1, v_2 \in V$, e $\alpha, \beta \in \F$, temos: \[ \psi((\alpha \varphi_1 + \beta \varphi_2) \otimes v)(u) = (\alpha \varphi_1(u) + \beta \varphi_2(u))v = \alpha \varphi_1(u)v + \beta \varphi_2(u)v, \] o que mostra a linearidade em $U^*$.
  - Similarmente, para combinações lineares em $V$, temos: \[ \psi(\varphi \otimes (\alpha v_1 + \beta v_2))(u) = \varphi(u)(\alpha v_1 + \beta v_2) = \alpha \varphi(u)v_1 + \beta \varphi(u)v_2, \] o que mostra a linearidade em $V$.
- Usando a propriedade universal do produto tensorial, existe uma aplicação linear $\tilde \psi:U^*\otimes V\to \mbox{Hom}(U,V)$ que estende $\psi$, ou seja, $\tilde\psi(\varphi\otimes v)=\psi(\varphi,v)$ vale para todo $\varphi\in U^*$ e $v\in V$.
$\psi$ é injetiva: Para mostrar que $\psi$ é injetiva, construiremos um inverso à direita para $\psi$. Definimos uma aplicação $\phi: \mbox{Hom}(U, V) \to U^* \otimes V$ da seguinte forma:
- Para cada $T \in \mbox{Hom}(U, V)$, definimos $\phi(T) = \sum_{i=1}^n \varphi_i \otimes T(u_i)$, onde $\{u_1, \ldots, u_n\}$ é uma base de $U$ e $\{\varphi_1, \ldots, \varphi_n\}$ é a base dual correspondente em $U^*$.
Agora, calculamos $\psi(\phi(T))$. Seja $u\in U$ e escreva $u=\alpha_1u_1+\cdots+\alpha_nu_n$. Note que $\alpha_i=\varphi_i(u)$ para todo $i$. Ora, \[ \psi(\phi(T))(u) = \psi\left(\sum_{i=1}^n \varphi_i \otimes T(u_i)\right)(u) = \sum_{i=1}^n \varphi_i(u) T(u_i)=\sum_{i=1}^n \alpha_i T(u_i)=T(u). \] Portanto, $\psi(\phi(T)) = T$, o que mostra que $\phi$ é um inverso à direita de $\psi$. Assim, $\psi$ é injetiva.
Isomorfismo no caso de dimensão finita: Quando $\dim U$ e $\dim V$ são finitas, $\dim (U^*\otimes V)=\dim\mbox{Hom}(U,V)=\dim U\cdot \dim V$ e uma aplicação linear injetiva entre estes dois espaços precisa ser um isomorphism. Logo $U^*\otimes V\cong \mbox{Hom}(U,V)$.

Exercício 64.40 [Adjunção Hom-Tensor] Sejam $U$, $V$ e $W$, vector spaces sobre $\F$. Mostre que \[ \mbox{Hom}(U\otimes V,W)\cong\mbox{Hom}(U,\mbox{Hom}(V,W)). \] [Dica: Defina duas aplicações $\alpha: \mbox{Hom}(U\otimes V,W)\to\mbox{Hom}(U,\mbox{Hom}(V,W))$ e $\beta:\mbox{Hom}(U,\mbox{Hom}(V,W))\to \mbox{Hom}(U\otimes V,W)$ da maneira mais natural possível e mostre que elas são inversas. Confira também a discussão na página math.stackexchange.com/q/1849098.]

Solução:

Definição de $\alpha$:
- Seja $\alpha: \mbox{Hom}(U \otimes V, W) \to \mbox{Hom}(U, \mbox{Hom}(V, W))$ definida por: \[ \alpha(T)(u)(v) = T(u \otimes v), \quad \forall T \in \mbox{Hom}(U \otimes V, W), \, u \in U, \, v \in V. \] A bilinearidade do produto tensorial implica que $\alpha(T)\in \mbox{Hom}(U, \mbox{Hom}(V, W))$ e é fácil verificar que $\alpha$ é linear.
Definição de $\beta$:
- Seja $S\in \mbox{Hom}(U, \mbox{Hom}(V, W))$. Defina a aplicação bilinear $\beta_S:U\times V\to W$ por $\beta_S(u,v)=S(u)(v)$. É fácil verificar que $\beta_S$ é bilinear. Pela propriedade universal do produto tensorial, existe único $\tilde\beta_S:U\otimes V\to W$ que estende $\beta_S$; ou seja $\tilde\beta_S(u\otimes v)=\beta_S(u,v)=S(u)(v)$ para todo $u\in U$ e $v\in V$. Seja $\beta: \mbox{Hom}(U, \mbox{Hom}(V, W)) \to \mbox{Hom}(U \otimes V, W)$ definida por: \[ S\mapsto \tilde \beta_S. \] Note que $\beta(S)(u\otimes v)=S(u)(v)$.
Mostrando que $\alpha$ e $\beta$ são inversas:
- Para $T \in \mbox{Hom}(U \otimes V, W)$, temos: \[ (\beta \circ \alpha)(T)(u \otimes v) = \alpha(T)(u)(v) = T(u \otimes v). \] Assim, $\beta \circ \alpha = \mbox{id}_{\textrm{Hom}(U \otimes V, W)}$.
- Para $S \in \mbox{Hom}(U, \mbox{Hom}(V, W))$, temos: \[ (\alpha \circ \beta)(S)(u)(v) = \beta(S)(u \otimes v) = S(u)(v). \] Assim, $\alpha \circ \beta = \mbox{id}_{\textrm{Hom}(U, \textrm{Hom}(V, W))}$.
Conclusão:
- Como $\alpha$ e $\beta$ são inversas, temos: \[ \mbox{Hom}(U \otimes V, W) \cong \mbox{Hom}(U, \mbox{Hom}(V, W)). \]

Exercício 64.41 [Produto tensorial como functor] Seja $W$ um $\F$-espaço vetorial e defina o functor $T_W$ na categoria de $\F$-espaços vetoriais da seguinte forma: \[ T_W(V)=V\otimes W\quad\mbox{se $V$ é um $\F$-espaço} \] e se $f:U\to V$ é uma transformação linear, então defina \[ T_W(f)=f\otimes \mbox{id}_W:U\otimes W\to V\otimes W \] onde $f\otimes \mbox{id}_W$ está definida como no Teorema 62.4.

O functor $T_W$ é covariante ou contravariante?
Mostre que se $f$ é injetiva/sobrejetiva, então $T_W(f)$ é injetiva/sobrejetiva, respetivamente.

Solução:

O functor $T_W$ é covariante. Isso ocorre porque, para cada transformação linear $f: U \to V$, o mapa $T_W(f) = f \otimes \mbox{id}_W$ preserva a direção da composição. Em outras palavras, se $g: V \to X$ é outra transformação linear, então: \[ T_W(g \circ f) = (g \circ f) \otimes \mbox{id}_W = (g \otimes \mbox{id}_W) \circ (f \otimes \mbox{id}_W) = T_W(g) \circ T_W(f). \] Isso mostra que $T_W$ é um functor covariante.
Injetividade de $T_W(f)$. Se $f$ é injetiva, ela possui uma inversa à esquerda $g: V \to U$ tal que $g(f(u)) = u$ para todo $u \in U$. Defina $T_W(g): V \otimes W \to U \otimes W$ como $g \otimes \mbox{id}_W$. Então, \[ T_W(g) \circ T_W(f) = (g\otimes \mbox{id}_W) \circ (f \otimes \mbox{id}_W) = (g \circ f) \otimes \mbox{id}_W = \mbox{id}_U \otimes \mbox{id}_W = \mbox{id}_{W \otimes W}. \] Assim, $T_W(f)$ possui uma inversa à esquerda e é injetiva. Se $f$ é sobrejetiva, então $T_W(f)$ é também sobrejetiva e isso pode ser verificado de maneira similar, usando inversa à direita.

Exercício 64.42 Sejam $U$, $V$, $X$ e $Y$ espaços vetoriais com bases $B_U$, $B_V$, $B_X$ e $B_Y$, respetivamente. Assuma que $f:U\to X$ e $g:V\to Y$ são lineares. Escreva a matriz \[[f\otimes g]^{B_U\otimes B_V}_{B_X\otimes B_Y} \] em termos das matrizes \[ [f]^{B_U}_{B_X}\quad \mbox{e}\quad [g]^{B_V}_{B_Y}. \] (Dica: Confira o produto de Kronecker de matrizes.)

Exercício 64.43 Seja $\sigma$ uma permutação do conjunto $X=\{1,\ldots,n\}$ e sejam $x_1,\ldots,x_n$ incôgnitas sobre $\Q$. Seja \[ \Phi_n=\prod_{i<j}(x_i-x_j)\in\Q[x_1,\ldots,x_n] \] e seja \[ \sigma(\Phi_n)=\prod_{i<j}(x_{\sigma(i)}-x_{\sigma(j)}). \] Mostre que $\sigma(\Phi_n)=(-1)^\sigma\Phi_n$.

Exercício 64.44 Seja $\sigma$ uma permutação do conjunto $X=\{1,\ldots,n\}$. Demonstre que $\sigma$ é uma permutação par se e somente se \[ |\{(i,j)\in X\times X\mid i<j\mbox{ mas }\sigma(i)>\sigma(j)\}| \] é um número par. Note que um par $(i,j)$ com $i<j$ mas $\sigma(i)>\sigma(j)$ chama-se inversão de $\sigma$. Dica: Use 64.43

Solução:

Para mostrar que $\sigma$ é uma permutação par se e somente se o número de inversões é par, note que cada inversão $(i, j)$ com $i < j$ e $\sigma(i) > \sigma(j)$ troca o sinal de $\sigma$. O número total de inversões determina o sinal de $\sigma$, sendo par para permutações pares e ímpar para permutações ímpares. Assim, a paridade do número de inversões coincide com a paridade de $\sigma$.

Exercício 64.45 Seja $V$ um espaço vetorial. Defina a $k$-ésima potência exterior $\Lambda^kV$ como um espaço vetorial junto com uma aplicação $k$-linear $\lambda:V^k\to \Lambda^kV$ que satisfaz a seguinte propriedade universal: Para todo espaço vetorial $Z$ e toda aplicação $k$-linear $f:V^k\to Z$, existe uma única aplicação linear $\tilde f:\Lambda^kV\to Z$ tal que $f = \tilde f\circ \lambda$.

Desegne o diagrama que corresponde à propriedade universal.
Demonstre que $\Lambda^kV$ é único a menos de isomorfismo.
Demonstre que $\Lambda^kV$ existe. [Dica: considere $W=(V\otimes\cdots\otimes V)/J$ (tomando o produto tensorial $k$-vezes) onde $J$ é o espaço gerado por elementos na forma $v_1\otimes\cdots\otimes v_k$ onde $v_i=v_j$ para algum $i\neq j$ e mostre que este espaço satisfaz a propriedade universal.]

Solução:

Diagrama da propriedade universal: O diagrama que representa a propriedade universal da $k$-ésima potência exterior $\Lambda^kV$ é o seguinte:
```
V^k  ----->  Z
 |            ^
 |            |
 v            |
Λ^kV --------> 
```
Aqui, a seta vertical $V^k \to \Lambda^kV$ é a aplicação $k$-linear $\lambda$, e a seta diagonal $\Lambda^kV \to Z$ é a aplicação linear $\tilde{f}$ que torna o diagrama comutativo, ou seja, $f = \tilde{f} \circ \lambda$.
Unicidade de $\Lambda^kV$: Seja $\Lambda^kV$ e $\Lambda'^kV$ dois espaços vetoriais que satisfazem a propriedade universal com as aplicações $k$-lineares $\lambda: V^k \to \Lambda^kV$ e $\lambda': V^k \to \Lambda'^kV$. Pela propriedade universal de $\Lambda^kV$, existe uma aplicação linear única $\phi: \Lambda^kV \to \Lambda'^kV$ tal que $\lambda' = \phi \circ \lambda$. Analogamente, pela propriedade universal de $\Lambda'^kV$, existe uma aplicação linear única $\psi: \Lambda'^kV \to \Lambda^kV$ tal que $\lambda = \psi \circ \lambda'$.

Compondo as duas aplicações, temos $\psi \circ \phi: \Lambda^kV \to \Lambda^kV$ tal que $\psi \circ \phi \circ \lambda = \lambda$. Pela unicidade da aplicação linear que satisfaz essa propriedade, segue que $\psi \circ \phi = \text{id}_{\Lambda^kV}$. Analogamente, $\phi \circ \psi = \text{id}_{\Lambda'^kV}$. Portanto, $\phi$ é um isomorfismo, mostrando que $\Lambda^kV$ é único a menos de isomorfismo.
Existência de $\Lambda^kV$: Considere o espaço $W = V \otimes \cdots \otimes V$ (produto tensorial $k$ vezes) e seja $J$ o subespaço de $W$ gerado pelos elementos da forma $v_1 \otimes \cdots \otimes v_k$ onde $v_i = v_j$ para algum $i \neq j$. Defina $\Lambda^kV = W / J$ e seja $\lambda: V^k \to \Lambda^kV$ a composição da aplicação canônica $k$-linear $V^k \to W$ com a projeção $W \to W / J$.

Para verificar que $\Lambda^kV$ satisfaz a propriedade universal, seja $f: V^k \to Z$ uma aplicação $k$-linear alternada. Pela propriedade universal do produto tensorial, existe único $\bar f:W\to Z$ que estende $f$. Como $f$ é $k$-linear alternada, $\bar f$ anula nos elementos de $J$. Assim, $\bar f$ induz uma aplicação linear $\tilde{f}: W/J\to Z$ tal que $f = \tilde{f} \circ \lambda$. A unicidade de $\tilde{f}$ segue do fato que os elementos da forma $v_1\otimes\cdots\otimes v_k+J$ geram $W/J$ e $\tilde f$ está determinado nestes tipos de elementos por $f$; de fato, \[ \tilde f(v_1\otimes\cdots\otimes v_k+J)=f(v_1,\ldots,v_k) \]

Exercício 64.46 Seja $V$ um espaço de dimensão finita e seja $B=\{b_1,\ldots,b_n\}$ uma base de $V$. Seja $\Lambda^kV$ a $k$-ésima potência exterior de $V$ com $\lambda:V^k\to \Lambda^kV$ sendo a aplicação $k$-linear canônica. Com $v_1,\ldots,v_k\in V$, denote $v_1\wedge\cdots\wedge v_k=\lambda(v_1,\ldots,v_k)$. Seja \[ \Lambda^kB=\{b_{i_1}\wedge\cdots\wedge b_{i_k}\mid 1\leq i_1<\cdots<i_k\leq n\}. \]

Demonstre que $\Lambda^kB$ é um conjunto gerador de $\Lambda^kV$.
Usando Lema 63.2, mostre que $\Lambda^kB$ é uma base de $\Lambda^kV$.
Determina a dimensão de $\Lambda^k V$ em termos de $n$ e $k$.

Exercício 64.47 Demonstre Lema 63.3.

Solução:

Seja $T \in A^k(V)$. Precisamos mostrar que $f^*T \in A^k(U)$, ou seja, que $f^*T$ é $k$-linear alternada.

$k$-linearidade:
- Seja $u_1, \ldots, u_k \in U$ e suponha que $u_i$ é substituído por $\alpha u_i + \beta u_i'$ para algum $i \in \{1, \ldots, k\}$, com $\alpha, \beta \in \F$ e $u_i' \in U$. Então: \[ f^*T(u_1, \ldots, \alpha u_i + \beta u_i', \ldots, u_k) = T(f(u_1), \ldots, f(\alpha u_i + \beta u_i'), \ldots, f(u_k)). \] Usando a $k$-linearidade de $T$ e a linearidade de $f$, temos: \[\begin{align*} &T(f(u_1), \ldots, \alpha f(u_i) + \beta f(u_i'), \ldots, f(u_k)) \\&= \alpha T(f(u_1), \ldots, f(u_i), \ldots, f(u_k)) + \beta T(f(u_1), \ldots, f(u_i'), \ldots, f(u_k)). \end{align*}\] Assim, $f^*T$ é $k$-linear.
Alternância:
- Seja $u_1, \ldots, u_k \in U$ com $u_i = u_j$ para algum $i \neq j$. Então: \[ f^*T(u_1, \ldots, u_k) = T(f(u_1), \ldots, f(u_k)). \] Como $u_i = u_j$, temos $f(u_i) = f(u_j)$. Como $T$ é alternada, segue que $T(f(u_1), \ldots, f(u_k)) = 0$. Portanto, $f^*T(u_1, \ldots, u_k) = 0$.

Concluímos que $f^*T \in A^k(U)$, e assim a restrição de $f^*$ resulta em uma aplicação linear $f^*_A: A^k(V) \to A^k(U)$.

Exercício 64.48 Usando a Definição 63.3, demonstre as propriedades comuns do determinante.

Se $f,g: V\to V$, então $\det (f\circ g)=\det f\cdot \det g$.
$\det f$ coincide com o determinante da matriz de $f$ em uma base de $V$.
$\det f=0$ se e somente se $f$ não é invertível.

Solução:

Propriedade multiplicativa do determinante:
- Seja $f, g: V \to V$. Pelo Definição 63.3, o determinante de $f$ é definido como o escalar $\delta \in \F$ tal que $f^*_A = \delta \cdot \text{id}_{A^n(V)}$, onde $A^n(V)$ é o espaço das formas $n$-lineares alternadas em $V$. Similarmente, para $g$, temos $g^*_A = \gamma \cdot \text{id}_{A^n(V)}$.
- Considere a composição $f \circ g$. O pullback $(f \circ g)^*_A$ é dado por: \[ (f \circ g)^*_A = g^*_A \circ f^*_A. \] Substituindo as expressões para $f^*_A$ e $g^*_A$, temos: \[\begin{align*} (f \circ g)^*_A &= (\gamma \cdot \text{id}_{A^n(V)}) \circ (\delta \cdot \text{id}_{A^n(V)}) \\&= (\gamma \cdot \delta) \cdot \text{id}_{A^n(V)}. \end{align*}\] Assim, $\det(f \circ g) = \det(f) \cdot \det(g)$.
A ser inserida.