82 Exercícios: Bloco 3

Exercício 82.1 Seja $\F$ um corpo e $\sigma$ um automorfismo de $\F$. Mostre que

$0^\sigma=0$;
$1^\sigma=1$;
$(-a)^\sigma=-(a^\sigma)$ para todo $a\in\F$;
$(b^{-1})^\sigma=(b^\sigma)^{-1}$ para todo $b\in\F\setminus\{0\}$.

Solução:

Mostrar que $0^\sigma = 0$:

Como $\sigma$ é um automorfismo, temos:
\[ 0^\sigma = (0 + 0)^\sigma = 0^\sigma + 0^\sigma. \]
Subtraindo $0^\sigma$ de ambos os lados, obtemos:
\[ 0 = 0^\sigma. \]
Mostrar que $1^\sigma = 1$:

Como $\sigma$ é um automorfismo, temos:
\[ 1^\sigma = (1 \cdot 1)^\sigma = 1^\sigma \cdot 1^\sigma. \]
Como $1^\sigma \neq 0$ (pois $\sigma$ é injetivo pela nossa conta anterior), podemos multiplicar ambos os lados por $(1^\sigma)^{-1}$:
\[ 1 = 1^\sigma. \]
Mostrar que $(-a)^\sigma = -(a^\sigma)$ para todo $a \in \mathbb{F}$:

Sabemos que $a + (-a) = 0$. Aplicando $\sigma$ a ambos os lados:
\[ a^\sigma + (-a)^\sigma = 0^\sigma = 0. \]
Portanto, $(-a)^\sigma$ é o inverso aditivo de $a^\sigma$, ou seja:
\[ (-a)^\sigma = -(a^\sigma). \]
Mostrar que $(b^{-1})^\sigma = (b^\sigma)^{-1}$ para todo $b \in \mathbb{F} \setminus \{0\}$:

Sabemos que $b \cdot b^{-1} = 1$. Aplicando $\sigma$ a ambos os lados:
\[ b^\sigma \cdot (b^{-1})^\sigma = 1^\sigma = 1. \]
Portanto, $(b^{-1})^\sigma$ é o inverso multiplicativo de $b^\sigma$, ou seja:
\[ (b^{-1})^\sigma = (b^\sigma)^{-1}. \]

(Caio Monteiro)

Exercício 82.2 Seja $\F=\Q$ ou $\F=\Z_p$ com $p$ primo. Mostre que o único automorfismo de $\F$ é $\mbox{id}_\F$.

Solução:

Caso $\mathbb{F} = \mathbb{Q}$

Seja $\sigma$ um automorfismo de $\mathbb{Q}$. Então:

Para $n \in \mathbb{Z}^+$, temos: \[ n^\sigma = (\underbrace{1 + \cdots + 1}_{n \text{ vezes}})^\sigma = \underbrace{1^\sigma + \cdots + 1^\sigma}_{n \text{ vezes}} = n \]
Para $-1$ observamos que: \[ 1 = 1^\sigma = (-1)^\sigma (-1)^\sigma \] Logo $((-1)^\sigma)^2 -1 = 0$. A equação $x^2 - 1$ só possui duas raízes sobre $\mathbb{Q}$, nomeadamente $1$ e $-1$. Como já sabemos que $1^\sigma = 1$, isso implica que $(-1)^\sigma = -1$.
Para $n \in \mathbb{Z}^-$, $n = -m$ com $m \in \mathbb{Z}^+$, então: \[ n^\sigma = (-m)^\sigma = (-1)^\sigma m^\sigma = -m = n \]

Logo $\sigma$ fixa todos os números inteiros.
Seja $b$ um número inteiro não nulo e $b^{-1}$ seu inverso em $\mathbb{Q}$. Pelo exercício anterior: \[ (b^{-1})^\sigma = (b^\sigma)^{-1} = b^{-1} \] onde a última igualdade vem das nossas considerações anteriores.
Para qualquer $ab^{-1} \in \mathbb{Q}$: \[ (ab^{-1})^{\sigma} = a^\sigma (b^{-1})^\sigma = ab^{-1} \]

Portanto, $\sigma$ fixa todos os números racionais, ou seja, $\sigma = \text{id}_{\mathbb{Q}}$.

Caso $\mathbb{F} = \mathbb{Z}_p$

Seja $\sigma$ um automorfismo de $\mathbb{Z}_p$. Como $\mathbb{Z}_p$ tem $p$ elementos e $\sigma$ é bijetora:

Temos que $0^\sigma = 0$ e $1^\sigma = 1$ (pelo Exercício 81.1)
Para $k \in \mathbb{Z}_p$, $k$ é igual à soma de $1$ uma quantidade $k$ de vezes: \[ k^\sigma = (\underbrace{1 + \cdots + 1}_{k \text{ vezes}})^\sigma = \underbrace{1^\sigma + \cdots + 1^\sigma}_{k \text{ vezes}} = k \]

Portanto, $\sigma = \text{id}_{\mathbb{Z}_p}$.

(Caio Monteiro)

Exercício 82.3 Seja $\sigma$ um automorfismo de $\R$. Mostre que

$x^\sigma\geq 0$ para $x\geq 0$;
$\sigma$ é crescente;
$\sigma$ é contínua;
$\Q\subseteq\mbox{Fix}(\sigma)$;
usando que $\Q$ é denso em $\R$, deduza que $\sigma=\mbox{id}_\R$.

Solução:

Mostrar que $x^\sigma \geq 0$ para $x \geq 0$

Se $x \geq 0$, então existe $y \in \mathbb{R}$ tal que $x = y^2$. Logo: \[ x^\sigma = (y^2)^\sigma = (y^\sigma)^2 \geq 0 \]
Mostrar que $\sigma$ é crescente

Sejam $a, b \in \mathbb{R}$ com $a < b$. Então:
- $b - a > 0$
- Pelo item anterior, $(b - a)^\sigma \geq 0$
- Mas $(b - a)^\sigma = b^\sigma - a^\sigma \geq 0$ ⇒ $b^\sigma \geq a^\sigma$
Além disso, se $b^\sigma = a^\sigma$, como $\sigma$ é injetiva, teríamos $b = a$, o que é uma contradição. Portanto, $b^\sigma > a^\sigma$.
Mostrar que $\sigma$ é contínua
- $\sigma$ é crescente (pelo item 2)
- Funções crescentes só podem ter descontinuidades do tipo salto
- Mas $\sigma$ é bijetiva, e descontinuidades do tipo salto violariam a sobrejetividade
  - (Imagine o gráfico com um salto: haveria valores no contradomínio que não seriam atingidos)
- Portanto, $\sigma$ não pode ter descontinuidades e é contínua
Mostrar que $\mathbb{Q} \subseteq \text{Fix}(\sigma)$

A demonstração é análoga ao caso $\mathbb{Q}$ no Exercício 81.2:
- Para qualquer $q \in \mathbb{Q}$, temos $q^\sigma = q$
- Portanto, $\mathbb{Q}$ está contido no conjunto dos pontos fixos de $\sigma$
Concluir que $\sigma = \text{id}_\mathbb{R}$

Seja $x \in \mathbb{R}$ arbitrário:
- Como $\mathbb{Q}$ é denso em $\mathbb{R}$, existe $(q_n) \subseteq \mathbb{Q}$ com $q_n \to x$
- Pela continuidade de $\sigma$: \[ x^\sigma = \left(\lim_{n \to \infty} q_n\right)^\sigma = \lim_{n \to \infty} q_n^\sigma = \lim_{n \to \infty} q_n = x \]
- Logo, $\sigma$ fixa todos os reais e portanto $\sigma = \text{id}_\mathbb{R}$

(Caio Monteiro)

Exercício 82.4 Seja $\sigma$ um automorfismo contínuo de $\C$. Mostre que

$\R\subseteq \mbox{Fix}(\sigma)$;
$\sigma=\mbox{id}_\C$ ou $\sigma$ é o conjugado complexo.

[Obs: $\C$ tem automorfismos que não são contínuos; veja a discussão no StackExchange.

Solução:

1. Mostrar que $\mathbb{R} \subseteq \text{Fix}(\sigma)$

Seja $x \in \mathbb{R}$. Como: - $\sigma$ é contínuo - $\sigma$ coincide com a identidade em $\mathbb{Q}$ (pelo Exercício 81.3) - $\mathbb{Q}$ é denso em $\mathbb{R}$

Então, tomando $(q_n) \subseteq \mathbb{Q}$ com $q_n \to x$, temos: \[ x^\sigma = \left(\lim_{n \to \infty} q_n\right)^\sigma = \lim_{n \to \infty} q_n^\sigma = \lim_{n \to \infty} q_n = x \]

Portanto, $\sigma$ fixa todos os números reais.

2. Mostrar que $\sigma = \text{id}_{\mathbb{C}}$ ou $\sigma$ é o conjugado complexo

Para qualquer $z = a + bi \in \mathbb{C}$ com $a,b \in \mathbb{R}$: - Pelo item anterior, $a^\sigma = a$ e $b^\sigma = b$

Para $i$, temos: \[ (i^2)^\sigma = (-1)^\sigma = -1 = (i^\sigma)^2 \] Logo $i^\sigma$ deve satisfazer $x^2 = -1$, portanto $i^\sigma = i$ ou $i^\sigma = -i$.

Caso 1: Se $i^\sigma = i$ \[ z^\sigma = (a + bi)^\sigma = a^\sigma + b^\sigma i^\sigma = a + bi = z \] Portanto $\sigma = \text{id}_{\mathbb{C}}$.

Caso 2: Se $i^\sigma = -i$ \[ z^\sigma = (a + bi)^\sigma = a^\sigma + b^\sigma i^\sigma = a - bi = \overline{z} \] Portanto $\sigma$ é o conjugado complexo.

Não existem outras possibilidades, pois as únicas raízes complexas de $x^2 = -1$ são $i$ e $-i$.

(Caio Monteiro)

Exercício 82.5 Seja $V$ um $\F$-espaço e denote por $\mbox{Bil}(V)$, $\mbox{Bil}_S(V)$, $\mbox{Bil}_A(V)$ os conjuntos das formas bilineares, bilieares simétricas, e bilineares alternadas sobre $V$.

Demonstre que $\mbox{Bil}(V)$, $\mbox{Bil}_S(V)$, $\mbox{Bil}_A(V)$ são espaços vetoriais com a soma e múltiplo escalar óbvia entre formas.
Assumindo que $\dim V=n$, mostre que \[\begin{align*} \mbox{Bil}(V)&\cong M_{n\times n}(\F);\\ \mbox{Bil}_S(V)&\cong \{A\in M_{n\times n}\mid A^t=A\};\\ \mbox{Bil}_A(V)&\cong \{A\in M_{n\times n}\mid A^t=-A\}\mbox{ se car}\,\F\neq 0.\\ \end{align*}\]
Determine $\dim \mbox{Bil}(V)$, $\dim \mbox{Bil}_S(V)$, $\dim\mbox{Bil}_A(V)$.

Esboço da solução:

Espaço vetorial:
Os conjuntos $\mbox{Bil}(V)$, $\mbox{Bil}_S(V)$ e $\mbox{Bil}_A(V)$ são subespaços vetoriais do espaço de todas as funções $V \times V \to \F$, pois a soma e o múltiplo escalar de formas bilineares (simétricas ou alternadas) continuam sendo formas bilineares (simétricas ou alternadas, respectivamente).
Isomorfismos com matrizes:
- Fixe uma base $\{e_1, \ldots, e_n\}$ de $V$. Toda forma bilinear $B$ é determinada pelos valores $B(e_i, e_j)$, que podem ser organizados na matriz de Gram $G_X(B) = (B(e_i, e_j))_{i,j}$. Assim, $\mbox{Bil}(V) \cong M_{n \times n}(\F)$, identificando cada forma bilinear com sua matriz de Gram. É fácil verificar que a identificação $B\mapsto G_X(B)$ é um isomorfismo $\operatorname{Bil}(V)\to M_{n\times n}(\F)$.
- $B$ é simétrica se $B(u, v) = B(v, u)$, o que equivale a $G_X(B)^t = G_X(B)$. Portanto, $\mbox{Bil}_S(V) \cong \{A \in M_{n \times n}(\F) \mid A^t = A\}$.
- $B$ é alternada se $B(v, v) = 0$ para todo $v$, o que implica que a diagonal de $G_X(B)$ é nula e $G_X(B)^t = -G_X(B)$. Assim, $\mbox{Bil}_A(V) \cong \{A \in M_{n \times n}(\F) \mid A^t = -A,\, a_{ii}=0\}$, supondo $\operatorname{car}(\F) \neq 2$.
Dimensões:

$\dim \mbox{Bil}(V) = n^2$, pois $\dim M_{n \times n}(\F)=n^2$.
$\dim \mbox{Bil}_S(V) = \frac{n(n+1)}{2}$, pois uma matriz simétrica é determinada pelos $n$ elementos da diagonal e pelos $\frac{n(n-1)}{2}$ elementos acima (ou abaixo) da diagonal.
$\dim \mbox{Bil}_A(V) = \frac{n(n-1)}{2}$, pois uma matriz alternada (com $a_{ii}=0$ e $a_{ij} = -a_{ji}$) é determinada apenas pelos elementos acima da diagonal, totalizando $\frac{n(n-1)}{2}$ parâmetros (válido se $\operatorname{car}(\F) \neq 2$).

Exercício 82.6 Seja $V$ um $\F$-espaço e denote por $\mbox{Bil}(V)$, $\mbox{Bil}_S(V)$, $\mbox{Bil}_A(V)$ os conjuntos das formas bilineares, bilieares simétricas, e bilineares alternadas sobre $V$.

Mostre que $\mbox{Bil}(V)\cong (V\otimes V)^*$.
Seja $\Lambda^2V$ a potência exterior definida no Exercício 64.45. Mostre que $\mbox{Bil}_A(V)\cong \Lambda^2(V)^*$.
Estude a definição de $\Lambda^2(V)$ no Exercício 64.45, e dê uma construção de um espaço vetorial $S^2(V)$ que satisfaz a mesma propriedade universal que $\Lambda^2(V)$, mas com funções $f:V\times V\to Z$ bilineares simétricas (em vez de alternadas). Mostre que $\mbox{Bil}_S(V)\cong S^2(V)^*$.

Esboço da solução:

Isomorfismo $\mbox{Bil}(V) \cong (V \otimes V)^*$:
Pela propriedade universal do produto tensorial, toda forma bilinear $B: V \times V \to \F$ corresponde unicamente a um funcional linear $\varphi_B: V \otimes V \to \F$ tal que $\varphi_B(v \otimes w) = B(v, w)$. Assim, $\mbox{Bil}(V) \cong (V \otimes V)^*$.
Isomorfismo $\mbox{Bil}_A(V) \cong (\Lambda^2 V)^*$:
Pelo Exercício 64.45, toda forma bilinear alternada $A: V \times V \to \F$ corresponde unicamente a um funcional linear $\psi_A: \Lambda^2 V \to \F$ tal que $\psi_A(v \wedge w) = A(v, w)$. Assim, $\mbox{Bil}_A(V) \cong (\Lambda^2 V)^*$.
Construção de $S^2(V)$ e isomorfismo $\mbox{Bil}_S(V) \cong (S^2 V)^*$:
Defina $S^2(V)$ como o quociente de $V \otimes V$ pelo subespaço gerado pelos elementos $v \otimes w - w \otimes v$. Assim, $S^2(V)$ satisfaz a propriedade universal para formas bilineares simétricas. Toda forma bilinear simétrica $S: V \times V \to \F$ corresponde unicamente a um funcional linear $\phi_S: S^2(V) \to \F$ tal que $\phi_S(v \odot w) = S(v, w)$, onde $v \odot w$ é a classe simétrica de $v \otimes w$. Portanto, $\mbox{Bil}_S(V) \cong (S^2 V)^*$.

Definição 82.1 Seja $\sigma$ um automorfismo de um corpo $\F$. Uma aplicação $f:V\to W$ entre $\F$-espaços vetoriais é chamada $\sigma$-semilinear, se $f(u+v)=f(u)+f(v)$ e $f(\alpha u)=\alpha^\sigma f(u)$ para todo $u,v\in V$ e $\alpha\in\F$.

Exercício 82.7 Seja $V$ um $\F$-espaço vetorial e $\sigma\in\mbox{Aut}(\F)$. Seja $\varphi: V\to V^*$ uma aplicação $\sigma$-semilinear e defina $B_\varphi:V\times V\to \F$ como \[ B_\varphi(u,v)=\varphi(v)(u). \]

Mostre que $B_\varphi$ é $\sigma$-sesquilinear.
Mostre que a aplicação $\varphi\mapsto B_\varphi$ é uma bijeção \[ \{\varphi: V\to V^*\mid \varphi\mbox{ é $\sigma$-semilinear}\}\to \{B: V\times V\to \F\mid B\mbox{ é $\sigma$-sesquilinear}\}. \]
Mostre que $\varphi$ é linear se e somente se $B_\varphi$ é bilinear.

Solução

$B_\varphi$ é $\sigma$-sesquilinear:
Seja $\varphi: V \to V^*$ uma aplicação $\sigma$-semilinear. Para $u, u' \in V$, $v, v' \in V$, $\alpha, \beta \in \F$:

Linearidade na primeira variável: Como $\varphi(v)\in V^*$ é linear, temos \[ B_\varphi(\alpha u + \beta u', v) = \varphi(v)(\alpha u + \beta u') = \alpha \varphi(v)(u) + \beta \varphi(v)(u') = \alpha B_\varphi(u, v) + \beta B_\varphi(u', v). \]
$\sigma$-semilinearidade na segunda variável: Como $\varphi:V\to V^*$ é $\sigma$-semilinear, temos \[ B_\varphi(u, \alpha v + \beta v') = \varphi(\alpha v + \beta v')(u) = (\alpha^\sigma \varphi(v) + \beta^\sigma \varphi(v'))(u) = \alpha^\sigma \varphi(v)(u) + \beta^\sigma \varphi(v')(u) = \alpha^\sigma B_\varphi(u, v) + \beta^\sigma B_\varphi(u, v'). \] Logo, $B_\varphi$ é $\sigma$-sesquilinear.

A aplicação $\varphi \mapsto B_\varphi$ é uma bijeção:

Injetividade: Se $B_\varphi = B_\psi$, então para todo $u, v \in V$, $\varphi(v)(u) = \psi(v)(u)$. Logo, $\varphi(v) = \psi(v)$ para todo $v$, ou seja, $\varphi = \psi$.
Sobrejetividade: Dado $B: V \times V \to \F$ $\sigma$-sesquilinear, defina $\varphi_B: V \to V^*$ por $\varphi_B(v)(u) = B(u, v)$.
- Para $v, v' \in V$, $\alpha, \beta \in \F$: \[ \varphi_B(\alpha v + \beta v')(u) = B(u, \alpha v + \beta v') = \alpha^\sigma B(u, v) + \beta^\sigma B(u, v') = \alpha^\sigma \varphi_B(v)(u) + \beta^\sigma \varphi_B(v')(u). \] Portanto, $\varphi_B$ é $\sigma$-semilinear e $B_{\varphi_B} = B$.
Assim, $\varphi \mapsto B_\varphi$ é uma bijeção entre aplicações $\sigma$-semilineares $V \to V^*$ e formas $\sigma$-sesquilineares $V \times V \to \F$.

$\varphi$ é linear se e somente se $B_\varphi$ é bilinear:

Se $\varphi$ é linear, então na segunda variável temos: \[ B_\varphi(u, \alpha v + \beta v') = \varphi(\alpha v + \beta v')(u) = \alpha \varphi(v)(u) + \beta \varphi(v')(u) = \alpha B_\varphi(u, v) + \beta B_\varphi(u, v'). \] Ou seja, $B_\varphi$ é bilinear.
Reciprocamente, se $B_\varphi$ é bilinear, então para todo $u \in V$: \[ \varphi(\alpha v + \beta v')(u) = B_\varphi(u, \alpha v + \beta v') = \alpha B_\varphi(u, v) + \beta B_\varphi(u, v') = \alpha \varphi(v)(u) + \beta \varphi(v')(u). \] Como isso vale para todo $u$, segue que $\varphi(\alpha v + \beta v') = \alpha \varphi(v) + \beta \varphi(v')$, ou seja, $\varphi$ é linear.

Exercício 82.8 Seja $V$ um espaço de dimensão finita com forma $\sigma$-sesquilinear reflexiva $B$. Seja $G$ a matriz de $B$ em uma base de $V$. Mostre que $\dim\mbox{Rad}(B)=\dim V-\mbox{posto}(G)$. Deduza que $B$ é não degenerada se e somente se $G$ é invertível.

Solução

Seja $V$ um espaço vetorial de dimensão finita e $B$ uma forma $\sigma$-sesquilinear reflexiva sobre $V$. Seja $G$ a matriz de Gram de $B$ em uma base de $V$.

O radical de $B$ é definido por \[ \mbox{Rad}(B) = \{v \in V \mid B(v, w) = 0 \text{ para todo } w \in V\}. \]

Na base escolhida, um vetor $v$ com coordenadas $[v]_X = (\alpha_1, \ldots, \alpha_n)^t$ pertence ao radical se e somente se \[ B(v, w) = ([v]_X)^t G ([w]_X)^\sigma = 0 \quad \text{para todo } w \in V. \] Isso equivale a dizer que $([v]_X)^t G = 0$, ou seja, $[v]_X$ está no núcleo (espaço nulo) da matriz $G^t$. As matrizes $G$ e $G^t$ têm o mesmo posto, portanto, \[ \dim \mbox{Rad}(B) = \dim \ker(G^t) = n - \operatorname{posto}(G^t) = n - \operatorname{posto}(G) = \dim V - \operatorname{posto}(G). \]

Em particular, $B$ é não degenerada se e somente se $\mbox{Rad}(B) = 0$, ou seja, se e somente se $\operatorname{posto}(G) = \dim V$, isto é, se $G$ é invertível.

Exercício 82.9 Denote por $H_2$ o espaço $\R^2$ com forma $B(e_1,e_1)=B(e_2,e_2)=0$ e $B(e_1,e_2)=B(e_2,e_1)=1$ na base canônica $\{e_1,e_2\}$ de $\R^2$.

Mostre que $H_2$ não é isométrico a $\R^2$ equipado com o produto interno usual.
Mostre que $H_2\perp H_2$ é isométrico a $\R^{2+2}$.

Solução

$H_2$ não é isométrico a $\R^2$ com o produto interno usual:

O produto interno usual em $\R^2$ é dado por $B_0(u,v) = u_1 v_1 + u_2 v_2$, cuja matriz na base canônica é a identidade: \[ G_0 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \] Já a matriz de $B$ em $H_2$ é \[ G = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \] O posto de ambas é $2$, mas as formas não são equivalentes: no produto interno usual, $B_0(e_1, e_1) = 1 \neq 0$, enquanto em $H_2$, $B(e_1, e_1) = 0$. Além disso, no produto interno usual, todo vetor não nulo tem $B_0(v, v) > 0$, enquanto em $H_2$ existem vetores não nulos isotrópicos, por exemplo $e_1$ e $e_2$. Portanto, não existe isometria entre $(\R^2, B)$ e $(\R^2, B_0)$.

$H_2 \perp H_2$ é isométrico a $\R^{2+2}$:

Considere $V = H_2 \oplus H_2$ com a forma $B((u_1, u_2), (v_1, v_2)) = B_{H_2}(u_1, v_1) + B_{H_2}(u_2, v_2)$. A matriz de $B$ em relação à base $\{e_1, e_2, f_1, f_2\}$ (onde $\{e_1, e_2\}$ é base do primeiro $H_2$ e $\{f_1, f_2\}$ do segundo) é \[ G' = \begin{pmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix} \] Esta matriz é simétrica e tem posto $4$. A base de $\R^{2+2}$ (ou seja, $\R^4$) na qual a matriz da forma $B$ correspondente a $H_2 \perp H_2$ é diagonal com duas entradas $1$ e duas entradas $-1$ pode ser explicitamente construída como segue:

Considere a base $\{e_1, e_2, f_1, f_2\}$ de $H_2 \perp H_2$, onde $e_1, e_2$ são a base do primeiro $H_2$ e $f_1, f_2$ do segundo. Defina os seguintes vetores: \[ \begin{aligned} u_1 &= \frac{1}{\sqrt{2}}(e_1 + e_2), \\ u_2 &= \frac{1}{\sqrt{2}}(e_1 - e_2), \\ u_3 &= \frac{1}{\sqrt{2}}(f_1 + f_2), \\ u_4 &= \frac{1}{\sqrt{2}}(f_1 - f_2). \end{aligned} \]

Nessa base, a matriz da forma $B$ é diagonal, com duas entradas $1$ e duas entradas $-1$: \[ B(u_1, u_1) = 1, \quad B(u_2, u_2) = -1, \quad B(u_3, u_3) = 1, \quad B(u_4, u_4) = -1, \] e todos os produtos cruzados são zero.

Portanto, a base explícita é $\{u_1, u_2, u_3, u_4\}$ conforme acima. Portanto, $H_2 \perp H_2$ é isométrico a $\R^{2+2}$.

Exercício 82.10 Seja $\F=\Z_p$ com $p\geq 3$ e $a,b \in \F$ com $a\neq 0$. Mostre que existem $u, v \in \F$ tais que $u^2 + a v^2 = b$.

Solução

Seja $Q=\{x^2\mid x\in \F\}$. Como $\F$ possui $p$ elementos com $p$ ímpar, temos que $|Q|=(p+1)/2$ (Lema 23.1). Se $a\neq 0$, então $|aQ|=(p+1)/2$ e $|b-aQ|=(p+1)/2$. Mas como $|\F|=p$, temos que \[ Q\cap (b-aQ)\neq \emptyset. \] Portanto existe elemento na inteerseção. Chamando este elemento de $u^2$, temos que $u^2=b-av^2$ com algum $v\in \F$ e assim \[ u^2+av^2=b. \]

Exercício 82.11 Seja $V$ um espaço vetorial sobre $\Z_p$ de dimensão maior ou igual a $3$ com uma forma bilinear simétrica.

Mostre que $V$ possui vetor não nulo isotrópico.
Mostre que a afirmação no item anterior não é verdadeira se $\dim V=1$ ou $\dim V=2$.

Solução

Assuma que $\dim V\geq 3$ e seja $b_1,\ldots,b_n$ uma base ortogonal de $V$ (existe por Teorema 75.1). Assuma que $a_i=Q(b_i)=B(b_i,b_i)$ para todo $i$. Se $Q(b_i)=0$ com algum $i$, então $b_i$ é vetor isotrópico, e o exercício está resolvido. Assuma que $Q(b_i)\neq 0$ para todo $i$. Sejam $u,v\in \Z_p$ tal que $u^2+(a_2/a_1)v^2=-a_3/a_1$; ou seja $u^2a_1+v_2a_2+a_3=0$ (existem por Exercício 82.11). Como $a_3\neq 0$, $(u,v)\neq (0,0)$. Seja $v=u b_1+vb_2+b_3$. Então \[ Q(v)=u^2a_1+v^2b_2+b_3=0. \] Temos que $v$ é vetor não nulo isotrópico.
Se $\dim V=1$ com base $\{b\}$, então $Q(\alpha b)=\alpha^2 Q(b)$. Então se escolhemos a forma em tal modo que $Q(b)=B(b,b)=1$, então não existe vetor não nulo isotrópico. Assuma que $\dim V=2$ com base $\{b_1,b_2\}$ seja $B$ uma forma bilinear sobre $V$ tal que $B(b_1,b_2)=B(b_2,b_1)=0$ e $B(b_1,b_1)=\delta_1$ e $B(b_2,b_2)=\delta_2$ tal que $-\delta_1/\delta_2$ não é quadrado. Ora, se $(u,v)\neq(0,0)$, então \[ Q(ub_1+vb_2)=u^2Q(b_1)+v^2Q(b_2)=u^2\delta_1+v^2\delta_2. \] Se $Q(ub_1+vb_2)=0$, então $v\neq 0$ e $-\delta_1/\delta_2=(u/v)^2$ que contradiz à escolha de $\delta_1,\delta_2$.

Exercício 82.12 Sejam $U$, $V$, $W$ espaços com formas $\sigma$-hermitianas, $f$ e $g$ transformações lineares tais que existem $f^*$ e $g^*$. Mostre que as seguintes afirmações estão válidas.

Se $\alpha,\beta\in\F$ e $f,g:V\to W$, então existe $(\alpha f+\beta g)^*$ e $(\alpha f+\beta g)^*=\alpha^\sigma f^*+\beta^\sigma g^*$.
Existe $(f^*)^*$ e $(f^*)^*=f$.
Se $f:U\to V$ e $g:V\to W$, então existe $(g\circ f)^*$ e $(g\circ f)^*=f^*\circ g^*$.
Existe $(\mbox{id}_V)^*$ para todo espaço $V$ e $(\mbox{id}_V)^*=\mbox{id}_V$.
Se $f:V\to W$ é invertível e existe $(f^{-1})^*$, então $(f^{-1})^*=(f^*)^{-1}$.

Solução

$(\alpha f+\beta g)^* = \alpha^\sigma f^* + \beta^\sigma g^*$:
Sejam $f, g: V \to W$ transformações lineares com adjuntas $f^*, g^*$. Pela definição de adjunto em espaços hermitianos: \[ B_W((\alpha f + \beta g)(v), w) = \alpha B_W(f(v), w) + \beta B_W(g(v), w) \] Como $B_W(f(v), w) = B_V(v, f^*(w))$ e $B_W(g(v), w) = B_V(v, g^*(w))$, temos: \[ B_W((\alpha f + \beta g)(v), w) = B_V(v, \alpha^\sigma f^*(w) + \beta^\sigma g^*(w))= B_V(v, (\alpha^\sigma f^* + \beta^\sigma g^*)(w)) \] Pela unicidade do adjunto, temos $(\alpha f + \beta g)^* = \alpha^\sigma f^* + \beta^\sigma g^*$.
$(f^*)^* = f$:
Pela definição, $B_W(f(v), w) = B_V(v, f^*(w))$ para todo $v, w$. Temos \[ B_V(f^*(w),v)=B_V(v, f^*(w))^\sigma = B_W(f(v), w)^\sigma=B_W(w,f(v)). \] Pela unicidado do adjunto, $(f^*)^* = f$.
$(g \circ f)^* = f^* \circ g^*$:
Para $f: U \to V$ e $g: V \to W$, temos: \[ B_W(g(f(u)), w) = B_V(f(u), g^*(w)) = B_U(u, f^*(g^*(w))) \] Logo, pela unicidade do adjunto, $(g \circ f)^* = f^* \circ g^*$.
$(\mbox{id}_V)^* = \mbox{id}_V$:
Para a identidade, $B_V(v, w) = B_V(v, w)$, então o adjunto da identidade é a própria identidade.
$(f^{-1})^* = (f^*)^{-1}$:
Segue do item anterior, pois \[ \mbox{id}_V=(\mbox{id}_V)^*=(f\circ f^{-1})^*=(f^{-1})^*\circ f^*. \] Obtemos por conta similar, que $\mbox{id}_V=f^*\circ (f^{-1})^*$. Portanto, $(f^{-1})^*=(f^*)^{-1}$.

Exercício 82.13 Sejam $\K$ e $\F$ corpos tais que $\K\subseteq \F$. Assuma que $V$ é um $\F$-espaço vetorial.

Mostre que $\F$ é um $\K$-espaço vetorial.
Mostre que $V$ é um $\K$-espaço vetorial.
Seja $B_\F$ uma base de $\F$ sobre $\K$ e seja $B_V$ uma base de $V$ sobre $\F$. Mostre que \[ \{\alpha b\mid \alpha \in B_\F\mbox{ e }b\in B_V\} \] é uma base de $V$ sobre $\K$.
Deduza que $\dim_\K V=\dim_\K \F\cdot \dim_\F V$.

Solução

$\F$ é um $\K$-espaço vetorial:
A soma e a multiplicação por escalares de $\K$ em $\F$ são herdadas da estrutura de corpo, e $\K \subseteq \F$. Assim, $\F$ é um espaço vetorial sobre $\K$.
$V$ é um $\K$-espaço vetorial:
Como $V$ é um $\F$-espaço vetorial e $\K\subseteq \F$, o múltiplo escalar com os elementos de $\K$ satisfaz os axiomas na definição de espaços vetoriais. Logo $V$ é um $\K$-espaço vetorial.
A família $\{\alpha b \mid \alpha \in B_\F,\, b \in B_V\}$ é base de $V$ sobre $\K$: Seja $B_\F$ uma base de $\F$ sobre $\K$ e $B_V$ uma base de $V$ sobre $\F$.

Gerador: Todo $v \in V$ pode ser escrito como $v = \sum_{i=1}^n \lambda_i b_i$ com $\lambda_i \in \F$, $b_i \in B_V$. Cada $\lambda_i$ pode ser escrito como combinação linear de elementos de $B_\F$ com coeficientes em $\K$, ou seja, $\lambda_i = \sum_{j=1}^m \alpha_{ij} \alpha_j$ com $\alpha_{ij} \in \K$, $\alpha_j \in B_\F$. Assim, \[ v = \sum_{i=1}^n \sum_{j=1}^m \alpha_{ij} (\alpha_j b_i), \] ou seja, $v$ é combinação linear sobre $\K$ dos elementos $\alpha_j b_i$.
Linearmente independente: Suponha $\sum_{i,j} \beta_{ij} (\alpha_j b_i) = 0$ com $\beta_{ij} \in \K$. Reescreva como $\sum_{i} \left( \sum_j \beta_{ij} \alpha_j \right) b_i = 0$. Como $B_V$ é base sobre $\F$, cada coeficiente $\sum_j \beta_{ij} \alpha_j = 0$ em $\F$. Como $B_\F$ é base de $\F$ sobre $\K$, segue que todos os $\beta_{ij} = 0$. Portanto, $\{\alpha b \mid \alpha \in B_\F,\, b \in B_V\}$ é base de $V$ sobre $\K$.

Fórmula das dimensões:
Se $m = \dim_\K \F$ e $n = \dim_\F V$, então \[ \dim_\K V = m \cdot n = \dim_\K \F \cdot \dim_\F V. \]

Exercício 82.14 Seja $f:V\to W$ uma aplicação $\sigma$-semilinear e assuma que $\dim_\F V=\dim_\F W$ e $\dim_{\textrm{Fix}(\sigma)}\F$ são todas finitas. Mostre que $f$ é sobrejetiva se e somente se $f$ é injetiva.

Solução

Seja $\K=\textrm{Fix}(\sigma)$. A aplicação $f$ é $\K$-linear. Além disso $\dim_{\K}V=\dim_\K\F\cdot \dim_\F V$ é finita. Ora, a afirmação segue pelo Teorema de Núcleo e Imagem para aplicações $\K$-lineares.

Exercício 82.15 Suponha que $V$ e $W$ são espaços vetoriais com formas $B_V$ e $B_W$ $\sigma$-hermitianas não degeneradas e seja $\alpha: V\to W$ uma transformação linear que possui adjunta $\alpha^\#:W\to V$. Na aula, definimos $\Phi_V:V\to V^*$ com a regra $v\mapsto B(-,v)$ e defina $\Phi_W$ na maneira análoga. Seja $\alpha^*:W^*\to V^*$ a transformação dual de $\alpha$. Mostre que o seguinte diagrama comuta:

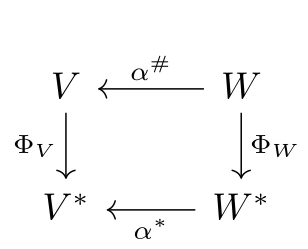
[Este exercício explica o comportamento similar do adjunto $\alpha^\#$ e o dual $\alpha^*$.]

Solução

Seja $B_V$ uma forma bilinear não degenerada em $V$ e $B_W$ uma forma bilinear não degenerada em $W$. Defina $\Phi_V: V \to V^*$ por $\Phi_V(v) = B_V(-, v)$ e $\Phi_W: W \to W^*$ por $\Phi_W(w) = B_W(-, w)$. Seja $\alpha: V \to W$ uma transformação linear com adjunta $\alpha^\#: W \to V$, isto é, \[ B_W(\alpha(v), w) = B_V(v, \alpha^\#(w)) \quad \text{para todo } v \in V,\, w \in W. \] Seja $\alpha^*: W^* \to V^*$ o dual de $\alpha$, isto é, $\alpha^*(\varphi) = \varphi \circ \alpha$ para $\varphi \in W^*$.

Queremos mostrar que o seguinte diagrama comuta: \[ \begin{array}{ccc} W & \xrightarrow{\Phi_W} & W^* \\ \alpha^\# \downarrow & & \downarrow \alpha^* \\ V & \xrightarrow{\Phi_V} & V^* \end{array} \] Ou seja, \[ \alpha^* \circ \Phi_W = \Phi_V \circ \alpha^\#. \]

Demonstração:

Para $w \in W$ e $v \in V$, \[ \begin{align*} (\alpha^* \circ \Phi_W)(w)(v) &= \alpha^*(\Phi_W(w))(v) \\ &= \Phi_W(w)(\alpha(v)) \\ &= B_W(\alpha(v), w) \end{align*} \] Por outro lado, \[ \begin{align*} (\Phi_V \circ \alpha^\#)(w)(v) &= \Phi_V(\alpha^\#(w))(v) \\ &= B_V(v, \alpha^\#(w)) \end{align*} \] Mas, pela definição de adjunto, $B_W(\alpha(v), w) = B_V(v, \alpha^\#(w))$ para todo $v \in V$, $w \in W$.

Portanto, \[ (\alpha^* \circ \Phi_W)(w) = (\Phi_V \circ \alpha^\#)(w) \] para todo $w \in W$, ou seja, o diagrama comuta.

Exercício 82.16 Seja $f:V\to W$ tal que $f$ possui adjunto $f^*$. Assumindo que $\dim V$ e $\dim W$ são finitas, mostre que $\ker f=\mbox{Im}(f^*)^\perp$ e $\mbox{Im}(f)=(\ker f^*)^\perp$. Quais destas afirmações vale nos casos quando a dimensão de $V$ ou a dimensão de $W$ é infinita?

Solução

Assuma que $f:V\to W$ é linear e possui adjunto $f^*:W\to V$, com $\dim V$ e $\dim W$ finitas. Seja $B_V$ e $B_W$ formas não degeneradas em $V$ e $W$.

Provar que $\ker f = \operatorname{Im}(f^*)^\perp$: Seja $v \in V$. Então \[\begin{align*} v \in \ker f&\Leftrightarrow\\ f(v) = 0&\Leftrightarrow\\ B_W(f(v),w)=0\mbox{ para todo }w\in W \mbox{($B_W$ é não degenerada) }&\Leftrightarrow\\ B_V(v,f^*(w))=0\mbox{ para todo }w\in W &\Leftrightarrow\\ v\perp f^*(w)\mbox{ para todo }w\in W &\Leftrightarrow\\ v\in \mbox{Im}(f^*)^\perp \end{align*}\]
Provar que $\operatorname{Im}(f) = (\ker f^*)^\perp$: Seja $y=f(v) \in \mbox{Im}(f)$. Se $w\in \ker{f^*}$, então \[ B_W(y,w)=B_W(f(v),w)=B_V(v,f^*(w))=B_V(v,0)=0. \] Logo $y\in (\ker{f^*})^\perp$ e obtemos que $\mbox{Im}(f)\leq (\ker{f^*})^\perp$. Afirmamos que quando $\dim V$ e $\dim W$ são finitas, então $\dim \mbox{Im}(f)=\dim (\ker{f^*})^\perp$. Segue do item 1. que, \[ \dim V-\dim \mbox{Im}(f)=\dim \ker f=\dim \operatorname{Im}(f^*)^\perp=\dim V-\dim \mbox{Im}(f^*). \] Ou seja, $\dim \mbox{Im}(f)=\dim \mbox{Im}(f^*)$. Por outro lado, \[ \dim (\ker f^*)^\perp=\dim W-\dim \ker f^*=\dim \mbox{Im}(f^*). \]
Caso de dimensão infinita:: A demonstração do item 1. não precisa que a dimensão seja finita. O argumento do item 2. precisa que as dimensões são finitas. Logo, item 1. vale com espaços de dimensão finita, enquanto item 2. pode não valer.

Exercício 82.17 Seja $f:V\to W$ uma transformação linear que possui adjunto e assuma que $\dim V$ e $\dim W$ são finitas. O espaço $\mbox{coker}(f)=W/\mbox{Im}(f)$ é chamado de conúcleo de $f$. Mostre que $\ker f\cong\mbox{coker}(f^*)$. Assumindo que $\dim V$ e $\dim W$ são finitas, deduza que \[\begin{align*} \dim \ker f&=\dim \ker f^*+\dim V-\dim W\\ \dim \mbox{Im}(f)&=\dim\mbox{Im}(f^*). \end{align*}\]

Solução

Seja $f:V\to W$ uma transformação linear entre espaços de dimensão finita, com adjunto $f^*:W\to V$. O conúcleo de $f$ é $\operatorname{coker}(f) = W/\operatorname{Im}(f)$.

Isomorfismo $\ker f \cong \operatorname{coker}(f^*)$: Segue do item 1. do Exercício 82.16 que \[ \dim \ker f=\dim \mbox{Im}(f^*)^\perp=V-\dim\mbox{Im}(f^*)= \dim V/\mbox{Im}(f^*)=\dim \mbox{coker}(f^*). \] Logo $\ker f\cong \mbox{coker}(f^*)$.
Fórmulas das dimensões: Temos que \[ \dim \ker f=\dim \mbox{coker}(f^*)=\dim V-\dim \mbox{Im}(f^*)=\dim V-\dim W+\dim\ker f^*. \] Ora, \[ \dim\mbox{Im}(f)=V-\dim\ker f=V-(\dim V-\dim W+\dim\ker f^*)=\dim W-\dim\ker f^*=\dim \mbox{Im}(f^*). \]

Exercício 82.18 Deduza do Exercício 82.17 que o posto coluna de uma matriz $m\times n$ com entradas em um corpo $\F$ é a mesma que o posto linha.

Solução

Seja $A$ uma matriz $m \times n$ com entradas em um corpo $\F$. Considere $A$ como a matriz na base canônica da transformação linear $f: \F^n \to \F^m$ dada por $f(x) = Ax$. O posto coluna de $A$ é $\dim \operatorname{Im}(f)$. O posto linha de $A$ coincide com o posto coluna de $A^t$ que é a matriz de $f^*$, onde $f^*: \F^m \to \F^n$ é o adjunto de $f$, considerando $\F^n$ e $\F^m$ com as formas bilineares standard. O posto coluna de $A^t$ é igual a $\dim \operatorname{Im}(f^*)$ Pelo Exercício 82.17, temos que $\dim \operatorname{Im}(f) = \dim \operatorname{Im}(f^*)$. Assim, o posto coluna de $A$ é igual ao posto linha de $A$.

Exercício 82.19 Seja $f:V\to W$ uma isometria de espaços de dimensão finita que possui adjunto. Mostre que $f\circ f^*=\mbox{id}_W$ e $f^*\circ f=\mbox{id}_V$.

Solução

Seja $f:V\to W$ uma isometria entre espaços de dimensão finita, com adjunto $f^*$. Como $f$ é isometria, temos para todo $v \in V$ e $w \in W$: \[ B_W(f(v), f(w)) = B_V(v, w). \]

Pela definição de adjunto, para todo $v \in V$ e $w \in W$: \[ B_W(f(v), w) = B_V(v, f^*(w)). \]

Agora, substitua $w$ por $f(u)$: \[ B_W(f(v), f(u)) = B_V(v, f^*(f(u))). \] Mas, pela isometria, \[ B_W(f(v), f(u)) = B_V(v, u). \] Logo, \[ B_V(v, f^*(f(u))) = B_V(v, u) \] para todo $v, u \in V$. Como $B_V$ é não degenerada, segue que $f^* \circ f = \operatorname{id}_V$.

Analogamente, trocando os papéis de $f$ e $f^*$, para todo $w, w' \in W$ existe $v \in V$ tal que $f(v) = w'$, e então: \[ B_W(w, w') = B_W(w, f(v)) = B_V(f^*(w), v) = B_W(f(f^*(w)), w'). \] Como isso vale para todo $w'$, segue que $f \circ f^* = \operatorname{id}_W$.

Portanto, \[ f^* \circ f = \operatorname{id}_V \quad \text{e} \quad f \circ f^* = \operatorname{id}_W. \]

Exercício 82.20 Considere \[ V=\{f:[-1,1]\to \R\mid f\mbox{ é contínua}\} \] com o forma bilinear \[ \langle f,g\rangle = \int_{-1}^1 f(t)g(t)\,dt. \] Mostre que as funções $\mbox{sen}(n\pi x)$, $\cos(n\pi x)$ com $n\in \Z$ formam um sistema ortonormal.

Exercício 82.21 Seja $V$ um $\C$-espaço vetorial de dimensão maior ou igual a $2$ e seja $B$ uma forma bilinear simétrica sobre $V$. Mostre que $V$ possui vetor isotrópico não nulo.

Solução

Seja $V$ um $\C$-espaço vetorial de dimensão maior ou igual a $2$ e $B$ uma forma bilinear simétrica sobre $V$. Seja $U\leq V$ um subespaço de dimensão $2$ e escolha uma base ortogonal $\{e_1, e_2\}$ de $U$ (existe por Teorema 75.1). Assuma que $B(e_i, e_i) = a_i$ para $i\in\{1,2\}$. Se $a_i = 0$ para algum $i$, então $e_i$ é isotrópico, e o exercício está resolvido.

Caso contrário, suponha que $a_i \neq 0$ para todo $i$. Considere o vetor $v = \alpha e_1 + \beta e_2$, onde $\alpha, \beta \in \C$. Temos: \[ B(v, v) = \alpha^2 a_1 + \beta^2 a_2. \] Queremos encontrar $\alpha, \beta \in \C$ não ambos nulos tais que $B(v, v) = 0$. Isso equivale a resolver a equação: \[ \alpha^2 a_1 + \beta^2 a_2 = 0. \] Dividindo por $a_1$, obtemos: \[ \alpha^2 + \frac{a_2}{a_1} \beta^2 = 0. \] Como $\C$ é algebricamente fechado, existe $\beta \neq 0$ tal que $\beta^2 = -a_1/a_2$. Escolha $\alpha = 1$. Assim, temos: \[ \alpha^2 + \frac{a_2}{a_1} \beta^2 = 1^2 -1 = 0. \] Logo, o vetor $v = e_1 + \beta e_2$ é isotrópico e não nulo.

Portanto, $V$ possui vetor isotrópico não nulo.

Exercício 82.22 Seja $\F$ um corpo de caraterística diferente de 2, denote por $I_{p+q+r}$ a matriz diagonal sobre $\F$ que tem $p$ entradas $−1$, $q$ entradas $1$ e $r$ entradas zero (nesta ordem) na diagonal principal. Seja $\sigma$ um automorfismo de $\F$ com $\sigma^2=\mbox{id}_\F$; no caso de $\F = \C$, seja $\bar z$ o conjugado complexo. Demonstre as seguintes afirmações:

Se $A \in M_{n\times n}(\F)$ com $A^t = A^\sigma$ , então existe uma matriz $X \in M_{n\times n}(\F)$ tal que $X^{σt}AX$ é diagonal.
Se $A \in M_{n\times n}(\F)$ com $A^t = A$, então existe uma matriz $X \in M_{n×n}(\F)$ tal que $X^tAX$ é diagonal.
Se $A \in M_{n×n}(\C)$ com $A^t = A$, então existe uma matriz $X \in M_{n×n}(\C)$ tal que $X^tAX = I_{0+q+r}$.
Se $A \in M_{n×n}(\C)$ com $A^t = \overline A$, então existe uma matriz $X \in M_{n×n}(\C)$ tal que $\overline X^tAX = I_{p+q+r}$.
Se $A \in M_{n×n}(\R)$ com $A^t = A$, então existe uma matriz $X \in M_{n×n}(\C)$ tal que $X^tAX = I_{p+q+r}$.

[Dica: Considere $A$ como matriz de Gram de alguma forma em $\F^n$ e seja $X$ uma matriz mudança debase.]

Solução

Seja $A \in M_{n \times n}(\F)$ com $A^t = A^\sigma$. Considere $V = \F^n$ com a forma $\sigma$-sesquilinear $B$ dada por $B(v, w) = v^t A w^\sigma$. Ora, \[ B(w,v)=w^tAv^\sigma=(w^tAv^\sigma)^t=v^{\sigma t}A^tw=v^{\sigma t}A^\sigma w=(v^t A^\sigma w^\sigma)^\sigma =B(v,w)^\sigma; \] ou seja $B$ é $\sigma$-hermitiana. Pelo Teorema 75.1, existe uma base ortogonal $\{e_1, \ldots, e_n\}$ de $V$ tal que $B(e_i, e_j) = 0$ para $i \neq j$. Seja $\overline X$ a matriz cujas colunas são os vetores da base ortogonal. Então, na nova base, a matriz de $B$ é diagonal e por Lema 74.3, $\overline X^{t} A \overline X^\sigma$ é diagonal. Ora, tome $X=X^\sigma$ e lembre que $\sigma^2=\mbox{id}_\F$.

A solução dos outros itens é similar.

Exercício 82.23 Seja $V$ um espaço vetorial com uma forma $\sigma$-sesquilinear simétrica $B$.

Assuma que $X$ é um sistema ortogonal composto por vetores não isotrópicos. Mostre que $X$ é L.I.
Seja $B$ uma base ortogonal de $V$ composta por vetores não isotrópicos e seja $v \in V$. Mostre que \[ v = \sum_{b∈B} \frac{B(v, b)}{B(b, b)} b \] e que a soma na linha anterior tem um número finito de somandos não nulos mesmo quando $\dim V$ é infinita.

Solução

$X$ é L.I.:
Seja $X$ um sistema ortogonal composto por vetores não isotrópicos. Suponha que $\sum_{i=1}^n \alpha_i x_i = 0$, com $\alpha_i \in \F$ e $x_i\in X$. Para cada $j$, temos: \[ B\left(\sum_{i=1}^n \alpha_i x_i, x_j\right) = B(0, x_j) = 0. \] Por linearidade de $B$, isso implica: \[ \sum_{i=1}^n \alpha_i B(x_i, x_j) = 0. \] Como $X$ é ortogonal, $B(x_i, x_j) = 0$ para $i \neq j$, e $B(x_j, x_j) \neq 0$ (pois $x_j$ não é isotrópico). Assim: \[ \alpha_j B(x_j, x_j) = 0. \] Como $B(x_j, x_j) \neq 0$, segue que $\alpha_j = 0$. Portanto, todos os $\alpha_i = 0$, e $X$ é L.I.
Representação de $v$:
Seja $X$ uma base ortogonal composta por vetores não isotrópicos. Se $v\in V$, então $v$ é combinação linear de vetores de $X$: \[ v=\sum_{i=1}^n \alpha_i b_i \tag{82.1}\] onde $\alpha_i\in \F$ e $b_i\in X$. Para cada $b \in X$, temos: \[ B(v, b) = B\left(\sum_{i=1}^n \alpha_ib_i,b\right)=\left\{\begin{array}{ll} \alpha_i B(b_i,b_i) & \mbox{se $b=b_i$ com algum $i$}\\ 0 & \mbox{caso contrário.}\end{array}\right. \] Ou seja, o coeficiente de $b\in X$ na combinação linear para $v$ na base $X$ é \[ \frac{B(v,b)}{B(b,b)}. \] Em particular, \[ v=\sum_{b\in X}\frac{B(v,b)}{B(b,b)} b \] e esta soma é finita, o coeficiente de $b$ será não nula apenas para os $b$ que aparecem na combinação linear na Equação 82.1.

Exercício 82.24 Revise o procedimento de ortogonalização de Gram-Schmidt e reflita se ele pode ser usado no contexto mais geral de formas $\sigma$-hermitianas não degeneradas.

Exercício 82.25 Seja $V = \R^4$ com formas alternadas $B_1$ e $B_2$ dadas pelas seguintes matrizes na base canônica: \[ G(B_1) = \begin{pmatrix} 0 & 1 & 1 & 1 \\ −1 & 0 & 1 & 1\\ −1 & −1 & 0 & 1\\ −1 & −1 & −1 & 0 \end{pmatrix} \quad \mbox{e}\quad G(B_2) = \begin{pmatrix} 0 & −1 & 0 & 0\\ 1 & 0 & −1 & 0\\ 0 & 1 & 0 & −1\\ 0 & 0 & 1 & 0\\ \end{pmatrix}. \] Mostre que $(V, B_1)$ e $(V, B_2)$ são isométricas.

Solução

Seja $e_1,e_2,e_3,e_4$ a base canônica de $\R^4$ e considere os seguintes vetores: \[\begin{align*} b_1&=(1,0,0,0);\\ b_2&=(1,1,0,0);\\ b_3&=(1,1,1,0);\\ b_4&=(1,1,1,1).\\ \end{align*}\] É fácil verificar que $b_1,b_2,b_3,b_4$ são l.i. e então eles formam uma base $X$ de $\R^4$. É uma conta fácil que a matriz de $B_2$ nesta base coincide com $G(B_1)$. Portanto \[ B_2(b_i,b_j)=B_1(e_i,e_j)\quad\mbox{para todo}\quad i,j\in\{1,\ldots,4\}. \] Considerando o isomorfismo $f$ que manda $b_i\mapsto e_i$ para todo $i$, temos que
$f$ é uma isometria $(\R^4,B_2)\to (\R^4,B_1)$.

Solução alternativa: Como $\det G(B_1)=\det G(B_2)=1$, temos que $B_1$ e $B_2$ são formas alternadas não degeneradas. Segue do Exercício 82.26 que $(\R^4,B_1)$ e $(\R^4,B_2)$ são somas diretas de dois planos hyperbólicos. Portanto, $(\R^4,B_1)$ e $(\R^4,B_2)$ são isométricos com o espaço $(\R^4,B)$ tal que a matriz de Gram de $B$ é \[ \begin{pmatrix} 0 & 1 & 0 & 0 \\ -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & -1 & 0\end{pmatrix} \] Como a isometria é uma relação de equivalência, temos que $(\R^4,B_1)$ e $(\R^4,B_2)$ são isométricos.

Exercício 82.26 Seja $V$ um $\F$-espaço vetorial de dimensão $2$ com forma alternada $B$. Um par hipérbólico é um par $e,f\in V$ tal que $B(e,e)=B(f,f)=0$ e $B(e,f)=1$. Um plano hiperbólico é um subespaço $H$ gerado por um par hiperbólico.

Mostre que quando $\dim V=2$ e $B$ é não degenerada, então $V$ é um plano hipérbólico.
Mostre que quando $\dim V$ é finita e $B$ é não degenerada, então $V$ é uma soma direta de planos hiperbólicos ortogonais 2 a 2.
Deduza que na situação do item 2., $\dim V$ é par.
Deduza que quando $n$ é par, existe uma única classe de isometria de $\F$-espaços de dimensão $n$ com formas alternadas não degeneradas.

Solução

$V$ é um plano hiperbólico quando $\dim V = 2$ e $B$ é não degenerada:
Seja $V$ um espaço vetorial de dimensão 2 com forma alternada não degenerada $B$. Escolha $e \in V$ não nulo
e note que $B(e, e) = 0$ (pois $B$ é alternada). Como $B$ é não degenerada, existe $f \in V$ tal que $B(e, f) \neq 0$. Multiplicando $f$ por um escalar apropriado, podemos assumir que $B(e, f) = 1$. Como $B$ é alternada, temos $B(f, f) = 0$. Assim, $\{e, f\}$ é um par hiperbólico, e $V$ é o plano hiperbólico gerado por $e$ e $f$.
$V$ é soma direta de planos hiperbólicos ortogonais quando $\dim V$ é finita e $B$ é não degenerada:
Seja $V$ um espaço vetorial de dimensão finita com forma alternada não degenerada $B$. Procedemos por indução em $\dim V$. Se $\dim V=1$ então $B$ é degenerada e o resultado segue do fato que a premissa é falsa. Se $\dim V=2$, então o resultado vale por item 1. Assuma que o resultado vale para espaços de dimensão menor que $\dim V$. Seja $e_1\in V$ não nulo e note que $B(e_1,e_1)=0$. Como $B$ é não degenerada, existe $f_1\in V$ tal que $B(e_1,f_1)\neq 0$. Tomando um múltiplo escalar adequado de $f_1$, podemos assumir que $B(e_1,f_1)=1$ e $B(f_1,f_1)=0$ (pois $B$ é alternada). Portanto $e_1,f_1$ é um par hiperbólico. Seja $H_1=\left<e_1,f_1\right>$. Como a restrição de $B$ para $H_1$ é não degenerada, temos que $V=H_1\oplus H_1^\perp$. Além disso, a restrição de $B$ para $H_1^\perp$ é alternada e não degenerada e por hipótese de indução, $H_1^\perp$ é soma direta de planos hiperbólicos \[ H_1^\perp=H_2\oplus\cdots \oplus H_m \] dois a dois ortogonais. Ora, temos que \[ V=H_1\oplus H_1^\perp =H_1\oplus H_2\oplus\cdots \oplus H_m \] onde os $H_i$ são planos hiperbólicos dois a dois ortogonais.
$\dim V$ é par:
Se $V$ é soma direta de $m$ planos hiperbólicos, então $\dim V = 2m$, que é par.
Única classe de isometria para $\dim V = n$ par:
Se $\dim V = n$ é par e $B$ é alternada e não degenerada, então $V$ é soma direta de $n/2$ planos hiperbólicos. Qualquer outro espaço vetorial de dimensão $n$ com forma alternada não degenerada também será soma direta de $n/2$ planos hiperbólicos. Assim, todos esses espaços são isométricos, e existe uma única classe de isometria.

Exercício 82.27 Seja $V$ um espaço vetorial de dimensão finita sobre $\Z_p$ com forma simétrica e não degenerada $B$ e assuma que $\dim V \geq 2$. Mostre que $V$ possui um elemento $v \in V$ tal que $Q(v) = B(v, v) = 1$. [Dica: Toma dois elementos $u, v \in V$ ortogonais não isotrópicos (justificando que eles existem). Vai precisar que $1$ pode ser escrito como combinação linear de quadrados; veja Exercício 82.10.]

Solução

Seja $V$ um espaço vetorial de dimensão finita sobre $\Z_p$ com forma simétrica e não degenerada $B$. Como $\dim V$ é finita, existe uma base ortogonal $\{e_1, e_2, \ldots, e_n\}$ de $V$ (pelo Teorema da Base Ortogonal). Assuma que $B(e_i, e_i) = a_i$ para todo $i$. Como $B$ é não degenerada, tem-se que $a_i\neq 0$ para todo $i$.

Escolha dois vetores ortogonais $e_1, e_2$ na base com $B(e_1, e_1) = a_1$ e $B(e_2, e_2) = a_2$. Como a base é ortogonal, temos $B(e_1, e_2) = 0$. Considere o vetor $v = u e_1 + v e_2$, onde $u, v \in \Z_p$. Temos: \[ B(v, v) = u^2 a_1 + v^2 a_2. \] Queremos encontrar $u, v \in \Z_p$ tais que $B(v, v) = 1$. Isso equivale a resolver a equação: \[ u^2 + v^2 \frac{a_2}{a_1} = \frac 1{a_1}. \] Esta equação tem solução por Exercício 82.10.

Exercício 82.28 Seja $V$ como no Exercício 82.27. Seja $a \in \Z_p$ um elemento fixo em $\Z_p \setminus \{x^2 \mid x \in \Z_p\}$. Mostre que existe uma base $X$ de $V$ tal que $G_X(B)$ é diagonal e as entradas na diagonal são ou $(1,\ldots, 1)$ ou $(1, \ldots , 1, a)$.

Solução

Note que se $x\in \Z_p\setminus\{0\}$, então $x=x_0^2$ ou $x=ax_0^2$ com algum $x_0$ (veja Lema 23.1).

Base da indução:
Para $\dim V = 1$, seja $b'$ base de $v$ e assuma que $B(b',b')=x\neq 0$ Escreva $x=x_0^2$ ou $x=ax_0^2$ com algum $x_0\in \Z_p$ e seja $b=x_0^{-1}b'$. Então $B(b,b)=1$ ou $B(b,b)=a$.

Passo indutivo:
Assuma que o resultado é válido para espaços de dimensão $n-1$. Seja $V$ um espaço vetorial de dimensão $n$ sobre $\Z_p$ com forma simétrica e não degenerada $B$. Escolha $v_1 \in V$ tal que $Q(v_1) = 1$ (existe por Exercício 82.27). Seja $H = \langle v_1 \rangle^\perp$, o subespaço ortogonal a $v_1$. Como $B$ é não degenerada, a restrição de $B$ a $H$ é uma forma simétrica e não degenerada, e $\dim H = n-1$. Pelo passo indutivo, existe uma base ortogonal $\{v_2, \ldots, v_{n}\}$ de $H$ tal que os valores de $B(v_i,v_i)$ são $1$ para $i\leq n-1$ e $B(v_n,v_n)=1$ ou $B(v_n,v_n)=a$.

Agora, considere a base $\{v_1, v_2, \ldots, v_{n}\}$ de $V$. A matriz de Gram de $B$ nesta base é diagonal com entradas $1, \ldots, 1$ ou $1, \ldots, 1, a$.

Exercício 82.29 Seja $f:V\to V$ um operador normal de um $\C$-espaço $V$ de dimensão finita. Assuma que todos os autovalores de $f$ são reais.

Mostre que $f$ é autoadjunto.
Deduza que quando $f:V\to V$ é um operador normal diagonalizável de um $\R$-espaço de dimensão finita, então ele é autoadjunto.

Solução

Mostrar que $f$ é autoadjunto:
Seja $f: V \to V$ um operador normal em um $\C$-espaço de dimensão finita, com todos os autovalores reais. Como $f$ é normal, existe uma base ortonormal de autovetores de $f$. Seja $X=\{v_1, \ldots, v_n\}$ essa base, com autovalores $\{\lambda_1, \ldots, \lambda_n\} \subseteq \R$. Logo a matriz de $f$ nesta base é \[ D=\begin{pmatrix} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_n \end{pmatrix} \] Como a base $X$ é ortonormal, a matriz de $f^*$ na base $X$ é $D^*=\overline D^t=D$. Portanto $f=f^*$ e $f$ é autoadjunto.
Deduza que operadores normais diagonalizáveis em $\R$ são autoadjuntos:
Seja $f: V \to V$ um operador normal diagonalizável em um $\R$-espaço de dimensão finita. Como $f$ é diagonalizável, seus autovalores são reais. Pelo item anterior, isso implica que $f$ é autoadjunto.

Exercício 82.30 Considere o operador $f:\C^2\to \C^2$ dada pela seguinte matriz na base canônica: \[ \begin{pmatrix} 1 & i \\ i & 1\end{pmatrix}. \]

Mostre que $f$ é normal, mas não é autoadjunto.
Ache uma matriz $P$ unitária, tal que $P^*AP$ é diagonal.

Solução

Mostrar que $f$ é normal, mas não autoadjunto:
A matriz de $f$ é: \[ A = \begin{pmatrix} 1 & i \\ i & 1 \end{pmatrix}. \] Para verificar se $f$ é normal, calculamos $AA^*$ e $A^*A$, onde $A^*$ é o conjugado transposto de $A$: \[ A^* = \begin{pmatrix} 1 & -i \\ -i & 1 \end{pmatrix}. \] \[ AA^* = \begin{pmatrix} 1 & i \\ i & 1 \end{pmatrix} \begin{pmatrix} 1 & -i \\ -i & 1 \end{pmatrix} = \begin{pmatrix} 2 & 0 \\ 0 & 2 \end{pmatrix}. \] \[ A^*A = \begin{pmatrix} 1 & -i \\ -i & 1 \end{pmatrix} \begin{pmatrix} 1 & i \\ i & 1 \end{pmatrix} = \begin{pmatrix} 2 & 0 \\ 0 & 2 \end{pmatrix}. \] Como $AA^* = A^*A$, $f$ é normal. Para verificar se $f$ é autoadjunto, verificamos se $A = A^*$. Como $A \neq A^*$, $f$ não é autoadjunto.
Encontrar uma matriz unitária $P$ tal que $PAP^*$ seja diagonal:
Os autovalores de $A$ são obtidos resolvendo $\det(A - \lambda I) = 0$: \[ \det\left(\begin{pmatrix} 1-\lambda & i \\ i & 1-\lambda \end{pmatrix}\right) = (1-\lambda)^2 - (-1) = \lambda^2 - 2\lambda+2. \] Os autovalores são $\lambda_1 = 1+i$ e $\lambda_2 = 1-i$. Os autovetores correspondentes são $v_1=(1,1)$ (para $\lambda_1$) e $v_2=(1,-1)$ (para $\lambda_2$).

Normalize os autovetores para obter uma matriz unitária $P$: \[ P = \frac 1{\sqrt 2}\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}. \] Então: \[ P^*AP = \begin{pmatrix} 1+i & 0 \\ 0 & 1-i \end{pmatrix}. \]

Exercício 82.31 Mostre que todo operador $f$ de um $\F$-espaço vetorial $V$ de dimensão finita com forma hermitiana não degenerada pode ser escrito como \[ f = f_1+f_2 \] onde $f_1$ é autoadjunto e $f_2$ é anti-autoadjunto (ou seja, $f_2^*=-f_2$).

Solução

Seja $f: V \to V$ um operador em um $\F$-espaço vetorial de dimensão finita. Podemos escrever $f$ como: \[ f = \frac{1}{2}(f + f^*) + \frac{1}{2}(f - f^*), \] onde $f^*$ é o adjunto de $f$.

$f_1 = \frac{1}{2}(f + f^*)$ é autoadjunto:
Para verificar que $f_1$ é autoadjunto, calculamos: \[ f_1^* = \left(\frac{1}{2}(f + f^*)\right)^* = \frac{1}{2}(f^* + (f^*)^*) = \frac{1}{2}(f^* + f) = f_1. \] Logo, $f_1$ é autoadjunto.
$f_2 = \frac{1}{2}(f - f^*)$ é anti-autoadjunto:
Para verificar que $f_2$ é anti-autoadjunto, calculamos: \[ f_2^* = \left(\frac{1}{2}(f - f^*)\right)^* = \frac{1}{2}(f^* - (f^*)^*) = \frac{1}{2}(f^* - f) = -f_2. \] Logo, $f_2$ é anti-autoadjunto.

Portanto, podemos decompor $f$ como: \[ f = f_1 + f_2, \] onde $f_1$ é autoadjunto e $f_2$ é anti-autoadjunto.

Exercício 82.32 Seja $V$ um espaço com forma $\sigma$-hermitiana não degenerada e $f:V\to V$ uma projeção (ou seja, $f^2=f$). Mostre que $f$ é autoadjunto se e somente se $V=\ker f\oplus \mbox{Im}(f)$ e $\ker f\perp \mbox{Im}(f)$. [Eu acho que $V$ não precisa ser de dimensão finita, mas se seu argumento precisar desta condição, pode assumir.]

Solução

Seja $f: V \to V$ uma projeção, ou seja, $f^2 = f$. Pelo Lema 67.1, temos que $V=\ker f\oplus \mbox{Im}(f)$. Assuma que $f$ é autoadjunto, ou seja, $f^* = f$. Segue do Exercício 82.16 que $\ker f=\mbox{Im}(f)^\perp$ então vale a decomposição de $V$.

Reciprocamente, assuma que $V = \ker f \oplus \operatorname{Im}(f)$ com $\ker f \perp \operatorname{Im}(f)$. Sejam $v=v_1+v_2$ e $w=w_1+w_2$ elementos de $V$ tais que $v_1,w_1\in\ker f$ e $v_2,w_2\in\mbox{Im}(f)$. Tem-se que \[ B(f(v),w)=B(v_2,w_1+w_2)=B(v_2,w_2) \] e, similarmente, \[ B(v,f(w))=B(v_1+v_2,w_2)=B(v_2,w_2). \] Logo, a unicidade do adjunto implica que $f=f^*$.

Exercício 82.33 Seja $\ell^2$ o $\R$-espaço de sequências $a=(a_1,a_2,a_3,\ldots)$ reais tal que \[ \sum_{i\geq 1}a_i^2< \infty \] considerado com produto interno \[ \left< a,b\right>=\sum_{i\geq 1}a_ib_i. \] (Não precisa provar fato que $\ell^2$ é um espaço vetorial com produto interno, mas quero que reflita sobre nisso pensando porque está certo.) Considere o operador \[ f:\ell^2\to \ell^2,\quad (a_1,a_2,a_3,\ldots)\mapsto (a_1,a_2/2,a_3/3,\ldots ). \]

Mostre que $f$ é autoadjunto.
Mostre que $f$ é injetivo.
Mostre que $f$ não é sobrejetivo. [Dica: a sequência $(1/n)_{n\geq 1}\in\ell^2$ não está na imagem de $f$.]
Deduza que o adjunto de um operador injetivo não precisa ser sobrejetivo em espaços de dimensão infinita. [Achei o exemplo na página math.stackexchange.com/q/269105.]

Solução

Mostrar que $f$ é autoadjunto:
Seja $f: \ell^2 \to \ell^2$ definido por $f(a_1, a_2, a_3, \ldots) = (a_1, a_2/2, a_3/3, \ldots)$. Para verificar se $f$ é autoadjunto, calculamos: \[ \langle f(a), b \rangle = \sum_{i \geq 1} \frac{a_i}{i} b_i = \sum_{i \geq 1} a_i \frac{b_i}{i} = \langle a, f(b) \rangle. \] Logo, $f$ é autoadjunto.
Mostrar que $f$ é injetivo:
Seja $f(a) = 0$. Isso implica que $\frac{a_i}{i} = 0$ para todo $i \geq 1$, ou seja, $a_i = 0$ para todo $i$. Portanto, $a = 0$, e $f$ é injetivo.
Mostrar que $f$ não é sobrejetivo:
Considere a sequência $b = (1/n)_{n \geq 1} \in \ell^2$. Suponha que existe $a \in \ell^2$ tal que $f(a) = b$. Isso implica que $\frac{a_n}{n} = \frac{1}{n}$ para todo $n \geq 1$, ou seja, $a_n = 1$ para todo $n$. No entanto, a sequência $(1, 1, 1, \ldots)$ não pertence a $\ell^2$, pois $\sum_{n \geq 1} a_n^2 = \sum_{n \geq 1} 1 = \infty$. Portanto, $b \notin \operatorname{Im}(f)$, e $f$ não é sobrejetivo.
Dedução:
Como $f$ é autoadjunto e injetivo, mas não sobrejetivo, concluímos que o adjunto de um operador injetivo não precisa ser sobrejetivo em espaços de dimensão infinita.

Exercício 82.34 Seja $\ell^2$ o mesmo espaço vetorial que no exercício anterior e seja \[ f:\ell^2\to \ell^2,\quad (a_1,a_2,a_3,\ldots)\mapsto (0,a_1,a_2,\ldots) \] o operador right shift.

Mostre que $f$ possui adjunto.
Mostre que $f$ é injetiva, enquanto $f^*$ é sobrejetiva.
Verifique se $f$ é normal.

Solução

Mostrar que $f$ possui adjunto:
Seja $f: \ell^2 \to \ell^2$ definido por $f(a_1, a_2, a_3, \ldots) = (0, a_1, a_2, \ldots)$. Para verificar se $f$ possui adjunto, consideramos o operador $f^*: \ell^2 \to \ell^2$ definido por $f^*(a_1, a_2, a_3, \ldots) = (a_2, a_3, a_4, \ldots)$. Para todo $x, y \in \ell^2$, temos: \[ \langle f(x), y \rangle = \sum_{i \geq 1} (f(x))_i y_i = \sum_{i \geq 2} x_{i-1} y_i = \sum_{i \geq 1} x_i y_{i+1} = \langle x, f^*(y) \rangle. \] Logo, $f^*$ é o adjunto de $f$.
Mostrar que $f$ é injetivo e $f^*$ é sobrejetivo:

Para verificar que $f$ é injetivo, suponha que $f(x) = 0$. Isso implica que $(0, x_1, x_2, \ldots) = 0$, ou seja, $x_i = 0$ para todo $i \geq 1$. Portanto, $x = 0$, e $f$ é injetivo.
Para verificar que $f^*$ é sobrejetivo, seja $y \in \ell^2$. Defina $x \in \ell^2$ por $x_i = y_{i+1}$ para todo $i \geq 1$. Então: \[ f^*(x) = (x_2, x_3, x_4, \ldots) = (y_1, y_2, y_3, \ldots) = y. \] Logo, $f^*$ é sobrejetivo.

Verificar se $f$ é normal:
Para verificar se $f$ é normal, calculamos $f f^*$ e $f^* f$: \[ f f^*(a_1, a_2, a_3, \ldots) = f(a_2, a_3, a_4, \ldots) = (0, a_2, a_3, \ldots), \] \[ f^* f(a_1, a_2, a_3, \ldots) = f^*(0, a_1, a_2, \ldots) = (a_1, a_2, a_3, \ldots). \] Como $f f^* \neq f^* f$, $f$ não é normal.

Exercício 82.35 Seja $\overline \ell^2$ o $\R$-espaço de sequências infinitas nas duas direções. Ou seja \[ \overline\ell^2=\{(a_i)_{i\in \Z}\mid a_i\in \R,\ \sum_{i\in\Z}a_i^2< \infty\}. \] O produto interno de $\overline\ell^2$ está definido como \[ \left<a,b\right>=\sum_{i\in \Z}a_ib_i. \] Defina $f$ como o operador right shift em $\overline\ell^2$: \[ f:\overline \ell^2\to \overline \ell^2,\quad (a_i)_{i\in \Z}\mapsto (a_{i-1})_{i\in \Z}. \]

Mostre que $f$ possui adjunto.
Mostre que $f$ é normal, mas não é autoadjunto.

Solução

Mostrar que $f$ possui adjunto:
Seja $f: \overline{\ell}^2 \to \overline{\ell}^2$ definido por $f((a_i)_{i \in \mathbb{Z}}) = (a_{i-1})_{i \in \mathbb{Z}}$. Para verificar se $f$ possui adjunto, consideramos o operador $f^*: \overline{\ell}^2 \to \overline{\ell}^2$ definido por $f^*((a_i)_{i \in \mathbb{Z}}) = (a_{i+1})_{i \in \mathbb{Z}}$. Para todo $x, y \in \overline{\ell}^2$, temos: \[ \langle f(x), y \rangle = \sum_{i \in \mathbb{Z}} (f(x))_i y_i = \sum_{i \in \mathbb{Z}} x_{i-1} y_i = \sum_{i \in \mathbb{Z}} x_i y_{i+1} = \langle x, f^*(y) \rangle. \] Logo, $f^*$ é o adjunto de $f$.
Mostrar que $f$ é normal, mas não autoadjunto:
Para verificar se $f$ é normal, calculamos $f f^*$ e $f^* f$: \[ f f^*((a_i)_{i \in \mathbb{Z}}) = f((a_{i+1})_{i \in \mathbb{Z}}) = (a_i)_{i \in \mathbb{Z}}, \] \[ f^* f((a_i)_{i \in \mathbb{Z}}) = f^*((a_{i-1})_{i \in \mathbb{Z}}) = (a_i)_{i \in \mathbb{Z}}. \] Como $f f^* = f^* f$, $f$ é normal.

Para verificar se $f$ é autoadjunto, verificamos se $f = f^*$. Como $f((a_i)_{i \in \mathbb{Z}}) = (a_{i-1})_{i \in \mathbb{Z}}$ e $f^*((a_i)_{i \in \mathbb{Z}}) = (a_{i+1})_{i \in \mathbb{Z}}$, temos $f \neq f^*$. Logo, $f$ não é autoadjunto.

Exercício 82.36 Seja $T:\R^3\to\R^3$ uma transformação ortogonal com $\det T=-1$. Mostre que

$T$ é uma reflexão em relação a um plano que passa pela origem; ou
$T$ é uma rotoreflexão (ou seja uma rotação por um eixo $k$ e ângulo $\vartheta$ seguida por uma reflexão em relação a um plano perpendicular a $k$).

Dê exemplo explícito para os dois casos.

Solução

Como $TT^*=T^*T=\mbox{id}_V$, temos que $T$ é normal e assim é diagonalizável. Sejam $\lambda_1,\lambda_2,\lambda_3$ os autovaores complexos de $T$. Sabemos que

$|\lambda_i|=1$;
$\lambda_1\lambda_2\lambda_3=-1$;
se $\lambda\in \C$ é autovalor então o conjugado $\overline\lambda$ é também autovalor.

As possibilidades para os autovalores de $T$ são

$\lambda_1=-1$ e $\lambda_2=\lambda_3=1$.
$\lambda_1=-1$, $\lambda_2=\cos \vartheta +i\sen\vartheta$, $\lambda_3=\cos \vartheta -i\sen\vartheta$.

Além disso, os autoespaços são ortogonais.

No caso 1, $T$ é reflexão em relação ao plano $V_1$ (autoespaço com autovalor 1). No caso 2, $T$ é a composição de uma reflexão pelo plano $V_{-1}^\perp$ e uma rotação por ângulo $\vartheta$ no redor da reta $V_{-1}$.

Exercício 82.37 Descreeve as possibilidades para os autovalores de um operador ortogonal de $\R^4$. Dê exemplo para todos os casos e destaque as possibilidades para as operadores de $\operatorname{SO}_4$.

Solução

Autovalores de operadores ortogonais em $\R^4$:

Os autovalores de um operador ortogonal $T: \R^4 \to \R^4$ têm módulo 1, pois $T$ preserva normas. Além disso, os autovalores podem ser reais ($\pm 1$) ou complexos conjugados ($e^{i\theta}, e^{-i\theta}$). As possibilidades são: - Quatro autovalores reais: $\{1,1,1,1\}$, $\{1,-1,-1,-1\}$, $\{1, 1, -1, -1\}$, $\{1, 1, 1, -1\}$, $\{-1,-1,-1,-1\}$. - Dois autovalores reais e dois complexos conjugados: $\{1,1,e^{i\theta}, e^{-i\theta}\}$, $\{1, -1, e^{i\theta}, e^{-i\theta}\}$, ou $\{-1, -1, e^{i\theta}, e^{-i\theta}\}$. - Quatro autovalores complexos conjugados: $\{e^{i\theta_1}, e^{-i\theta_1}, e^{i\theta_2}, e^{-i\theta_2}\}$.

82.0.1 Exemplos para cada caso de operadores ortogonais em $\R^4$

82.0.1.1 Caso especial para $\operatorname{SO}_4$

Para $\operatorname{SO}_4$, o determinante é $1$, então os autovalores devem satisfazer a condição de produto $\lambda_1 \lambda_2 \lambda_3 \lambda_4 = 1$.

Exercício 82.38 Assista os vídeos de 3Blue1Brown nos links youtu.be/d4EgbgTm0Bg e youtu.be/zjMuIxRvygQ sobre os quaternions e sua ligação com $SO_3$. [Se precisar, pode ligar as legendas auto-geradas em português.]

Exercício 82.39 Denote por $SU_2$ o grupo de matrizes unitárias $2\times 2$ com entradas em $\C$ e com determinante $1$. Para cada quatérnio unitário $q=a+bi+cj+dk$, denote por $A_q$ a matriz \[ \begin{pmatrix} a+ib & c+id \\ -c+id & a-ib\end{pmatrix}. \]

Verifique que $A_q\in SU_2$.
Verifique que $\psi:q\mapsto A_q$ é um homomorfismo de grupos; ou seja, $A_{q_1q_2}=A_{q_1}A_{q_2}$.
Demonstre que o mapa $\psi: q\mapsto A_q$ é uma bijeção entre o grupo de quatérnios unitários e $SU_2$.

Exercício 82.40 Seja $f:\R^n\to\R^n$ uma isometria (ou seja $f$ preserva distância em $\R^n$) tal que $f(0)=0$.

Mostre que $f$ preserva norma.
Mostre que $f$ é linear e deduza que $f$ é uma transformação ortogonal. [Dica, mostre que $\|f(\alpha v)-\alpha f(v)\|=0$ e $\|f(u+v)-f(u)-f(v)\|=0$ para todo $u,v\in \R^n$ e $\alpha\in \R$.]

Dica

Consulta as notas da aula.

Exercício 82.41 Seja $f:\R^n\to \R^n$ uma isometria. Mostre que $f$ é a composição de uma translação ($T_w:\R^n\to\R^n$, $v\mapsto v+w$ para todo $v$) e uma transformação ortogonal.

Solução

Seja $f: \R^n \to \R^n$ uma isometria. Por definição, $f$ preserva distâncias, ou seja, para todo $u, v \in \R^n$: \[ \|f(u) - f(v)\| = \|u - v\|. \]

Decomposição de $f$:

Seja $w = f(0)$. Defina $T_w: \R^n \to \R^n$ como a translação por $w$, ou seja: \[ T_w(v) = v + w. \] Considere a função $g: \R^n \to \R^n$ dada por: \[ g(v) = f(v) - w. \] Então, para todo $u, v \in \R^n$: \[ \|g(u) - g(v)\| = \|f(u) - w - (f(v) - w)\| = \|f(u) - f(v)\| = \|u - v\|. \] Logo, $g$ preserva distâncias e satisfaz $g(0) = 0$.

$g$ é uma transformação ortogonal:

Pelo Exercício 82.40, toda isometria que fixa a origem é linear e ortogonal. Assim, $g$ é uma transformação ortogonal.

Conclusão:

Como $f(v) = g(v) + w$, temos que $f$ é a composição de uma translação $T_w$ e uma transformação ortogonal $g$: \[ f(v) = T_w(g(v)). \]

82 Exercícios: Bloco 3

82.0.1 Exemplos para cada caso de operadores ortogonais em \(\R^4\)

82.0.1.1 Caso especial para \(\operatorname{SO}_4\)