56 Computações com Python III

56.1 O espaço de funções analíticas

Sejam \(a,b\in\R\) com \(a<b\) e considere e espaço vetorial \(C^\infty[a,b]\) de funções analíticas no intervalo \([a,b]\). O espaço \(C^\infty[a,b]\) é espaço com produto interno onde o produto interno para \(f,g\in C^\infty[a,b]\) é definido como \[ \left<f,g\right>=\int_a^b fg\, dx. \tag{56.1}\] Hoje, nós vamos fazer algumas computações no espaço \(C^\infty[a,b]\).

Exemplo 56.1 Ponha, por exemplo, \(a=-1\), \(b=1\). Vamos verificar que as funções \(f(x)=x\) e \(g(x)=x^2\) são ortogonais.

from sympy import integrate, var, cos, sin, pi, Integral, plot
x = var('x')
f, g = x, x**2
integrate( f*g, (x,-1,1))
0

Observe como a função integrate está usada para calcular a integral.

Exercício 56.1 Escreva uma função inner_product(f, g, var, a, b) que devolve o produto interno das funções \(f\) e \(g\) sobre o intervalo \([a,b]\). A sua função deve verificar os seguintes valores.

inner_product( x, x**2, x, -1, 1 )
0
inner_product( 1, x**2, x, -1, 1 )
2/3
inner_product( cos(x), sin(x), x, -pi, pi )
0
inner_product( cos(x), cos(x), x, -pi, pi )
𝜋

Exercício 56.2 Escreva uma função orthogonal_projection(f, g, var, a, b) para calcular a projeção ortogonal de \(f\) sobre \(g\) (Proposição 51.1) considerando o produto interno na Equação 56.1. Use a função inner_product que escreveu no Exercício 56.1. A sua implementação deve verificar as seguintes computações.

orthogonal_projection( x, x**2, x, -1, 1 )
0
orthogonal_projection( 1, x**2, x, -1, 1 )
5x^2/3
orthogonal_projection( x**2, cos(x), x, -pi, pi )
−4cos(𝑥)

56.2 Ortogonalização de Gram-Schmidt

O processo de ortogonalização de Gram-Schmidt está descrita na demonstração do Teorema 51.1. Vamos revisar o processo aqui rapidamente. Assuma que \(v_1,\ldots,v_n\) é um sistema L.I. em um espaço vetorial \(V\) com produto interno. Defina os vetores \(w_1,\ldots,w_n\) da seguinte forma: \[\begin{align*} w_1&=v_1;\\ w_2&=v_2-\mbox{proj}_{w_1}(v_2);\\ w_3&=v_3-\mbox{proj}_{w_1}(v_3)-\mbox{proj}_{w_2}(v_3);\\ &\vdots\\ w_n&=v_n-\mbox{proj}_{w_1}(v_n)-\mbox{proj}_{w_2}(v_n)-\cdots-\mbox{proj}_{w_{n-1}}(v_n). \end{align*}\] Então o sistema \(w_1,\ldots,w_n\) é ortogonal e os subespaços \(\left<v_1,\ldots,v_i\right>\), \(\left<w_1,\ldots,w_i\right>\) são iguais para todo \(i\in\{1,\ldots,n\}\).

Exercício 56.3 Escreva uma função gram_schmidt(funcs, var, a, b) que, dada uma lista funcs de funções (assumindo que elas são L.I.), aplica o processo de ortogonalização de Gram-Schmidt para esta lista. A sua função deve verificar as seguintes computações.

gram_schmidt([1,x,x**2], x, -1, 1)
[1, x, x**2 - 1/3]
gram_schmidt([1,x,x**2], x, 0, 1)
[1, x - 1/2, x**2 - x + 1/6]
gram_schmidt([1,cos(x),sin(x)], x, -pi, pi)
[1, cos(x), sin(x)]

Dica: Cria uma lista ws para guardar as funções \(w_1,\ldots,w_n\). Assumindo que as funções \(w_1,\ldots,w_{k}\) foram calculadas e estão na lista ws, o próximo elemento de ws pode ser calculado com

f - sum(orthogonal_projection(f, w, var, a, b) for w in ws)

onde f é o elemento atual de funcs.

Exercício 56.4 Usando a função gram_schmidt no Exercício 56.3, calcule uma base ortogonal para o espaço \(\R_4[x]\) considerando o produto interno na Equação 56.1 sobre o intervalo \([-1,1]\) e sobre o intervalo \([0,1]\). Verifique com a função inner_product escrita no Exercício 56.1 que as funções no output são de fato ortogonais.

56.3 As séries de Fourier

Para calcular as séries de Fourier de algumas funções como no Teorema 52.1, vamos primeiro aprender como calcular integrais numericamente.

integrate( cos(x)*sin(x), (x, -2, 1))
-sin^2(2)/2+sin(1)/2
integrate( cos(x)*sin(x), (x, -2, 1)).evalf()
−0.0593741960791174
Integral(cos(x)*sin(x),(x,-2,1))
...integral object...
Integral( cos(x)*sin(x), (x, -2, 1)).evalf()
−0.0593741960791174

Consulte o manual para mais informações.

Exercício 56.5 Modifique a sua implementação do produto interno e projeção ortogonal no Exercício 56.1 e no Exercício 56.2 tal que elas devolvam aproximações numéricas em vez de valores exatos.

Exercício 56.6 Escreva uma função fourier(f) em Python que dada uma função \(f\in C^\infty[a,b]\), calcula a aproximação de Fourier para a função \(f\) até grau \(5\). Use a função orthogonal_projection modificada no Exercício 56.5. A sua função deve verificar as seguintes computações.

fourier(x)
2.0sin(𝑥)−1.0sin(2𝑥)+0.666666666666667sin(3𝑥)−0.5sin(4𝑥)+0.4sin(5𝑥)
fourier(x**2)
−4.0cos(𝑥)+1.0cos(2𝑥)−0.444444444444444cos(3𝑥)+0.25cos(4𝑥)−0.16cos(5𝑥)+3.28986813369645
fourier(abs(x))
−1.27323954473516cos(𝑥)−0.141471060526129cos(3𝑥)−0.0509295817894065cos(5𝑥)+1.5707963267949

Exercício 56.7 Verifique visualmente a qualidade destas aproximações. Por exemplo

f = abs(x)
plot(f, xlim=(-3,3), ylim=(-1,4))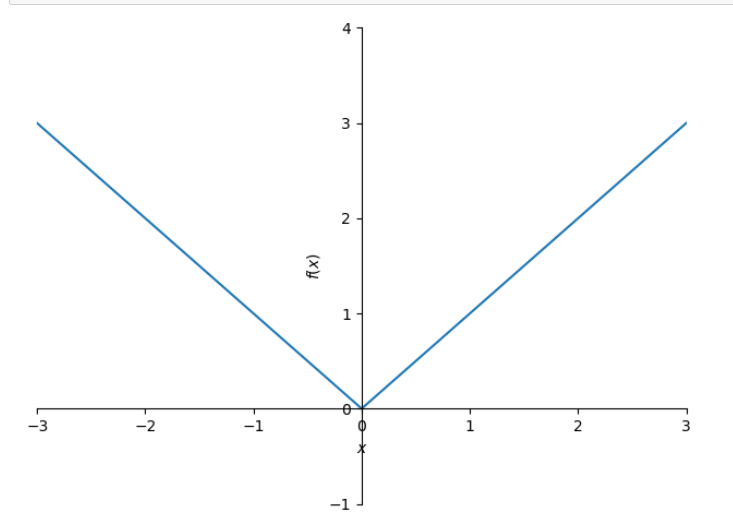

ff = fourier(f)
plot(ff, xlim=(-3,3), ylim=(-1,4))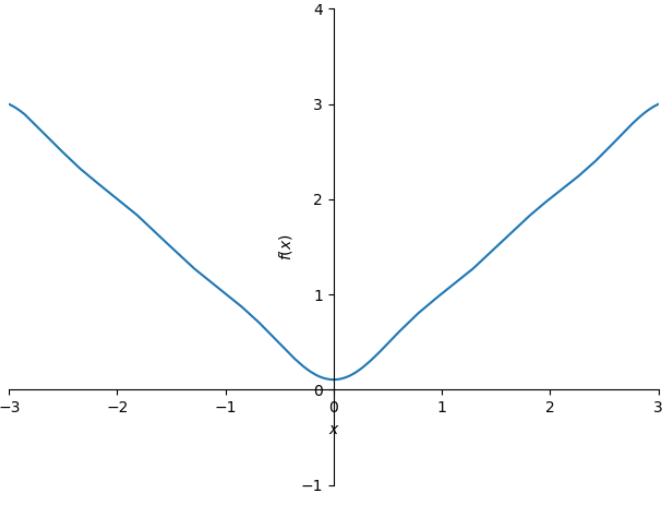

Faça a mesma coisa com outras funções, tais como \(x\), \(x^2\), \(\exp(x)\), etc.
Modifique a sua função fourier tal que seja capaz de calcular as aproximações até grau \(10\) ou até um grau \(k\) arbitrário fornecido pelo usuário.
Verifique se a qualidade das aproximações melhora assim que \(k\) aumenta.