\[ \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\R}{\mathbb R} \newcommand{\C}{\mathbb C} \newcommand{\F}{\mathbb F} \newcommand{\K}{\mathbb K} \newcommand{\L}{\mathbb L} \newcommand{\N}{\mathbb N} \newcommand{\sym}[1]{\operatorname{Sym}(#1)} \newcommand{\GLV}[1]{\operatorname{GL}(#1)} \newcommand{\SLV}[1]{\operatorname{SL}(#1)} \newcommand{\GL}[2]{\operatorname{GL}(#1,#2)} \newcommand{\SL}[2]{\operatorname{SL}(#1,#2)} \newcommand{\lxor}{\dot\lor} \newcommand{\cond}{\Rightarrow} \newcommand{\bicond}{\Leftrightarrow} \newcommand{\mdc}[2]{\operatorname{mdc}(#1,#2)} \newcommand{\grau}[1]{\operatorname{grau}(#1)} \newcommand{\real}[1]{\mathfrak R(#1)} \newcommand{\imag}[1]{\mathfrak I(#1)} \newcommand{\argz}[1]{\mbox{arg}(#1)} \DeclareMathOperator{\sen}{sen} \newcommand{\cis}[1]{\cos #1+i\sen #1} \newcommand{\E}{\mathbb E} \newcommand{\aut}[1]{\textrm{Aut}(#1)} \newcommand{\fix}[1]{\textrm{Fix}(#1)} \newcommand{\gal}[2]{\textrm{Gal}(#1:#2)} \newcommand{\overbar}[1]{\mkern 1.5mu\overline{\mkern-1.5mu#1\mkern-1.5mu}\mkern 1.5mu} \newcommand{\ul}[1]{\underline{#1}} \newcommand{\tn}[1]{\textnormal{#1}} \]
107 O Teorema Fundamental da Teoria de Galois
107.1 Evariste Galois
107.2 O Teorema Fundamental
Teorema 107.1 (Teorema Fundamental da Teoria de Galois) Seja \(\E:\F\) uma extensão de Galois finita. Seja \(\K\) um subcorpo de \(\E\) tal que \(\F\subseteq\K\).
- \(\E:\K\) é uma extensão de Galois finita e \(\gal\E\K\) é um subgrupo de \(\gal\E\F\).
- O mapa \(\gal{\E}-\) é uma bijeção do conjunto de corpos \(\K\) tais que \(\F\subseteq\K\subseteq\E\) para o conjunto de subgrupos de \(\gal\E\F\). Esta bijeção preserva normalidade (de subgrupos e extensões) e reverte inclusão no sentido que \(\K_1\subseteq \K_2\) se e somente se \(\gal\E{\K_1}\supseteq\gal\E{\K_2}\).
- A extensão \(\K:\F\) é normal se e somente se \(\gal\E\K\) é um subgrupo normal de \(\gal\E\F\). Neste caso \(\gal\K\F\cong \gal\E\F/\gal\E\K\).
Comprovação.
A primeira afirmação foi provada no Lema 106.7. Observe que \[ \gal\E\K=\{\varphi\in\aut \E\mid \K\subseteq\fix\varphi\}\leq \gal\E\F. \]
Seja \(G=\gal\E\F\) e ponha \[ \mathcal K=\{\K\subseteq \E\mid \F\subseteq \K\}\quad \mbox{e}\quad \mathcal G=\{H\leq G\}. \] Note que \(\gal\E-\) é uma aplicação \(\mathcal K\to \mathcal G\). Considere a aplicação \(\fix -:\mathcal G\to \mathcal K\). Mostremos que \(\gal\E-\circ \fix- = \mbox{id}_{\mathbb G}\) e \(\fix -\circ \gal\E-=\mbox{id}_{\mathcal K}\). O fato que \(\fix -\circ \gal\E-=\mbox{id}_{\mathcal K}\) segue to Teorema 106.2. Precisa-se provar que \(\gal\E-\circ \fix- = \mbox{id}_{\mathbb G}\); ou seja, se \(H\leq G\), então \(\gal \E{\fix H}=H\). Claramente, \(H\leq \gal \E{\fix H}\). Por outro lado, assuma que \(\E=\fix H(\alpha)\) com algum \(\alpha\in\E\) (Lema 106.5). O Lema 106.6 implica que \(\dim_{\fix H}\E\leq |H|\), portanto \[ |\gal \E{\fix H}|\leq \dim_{\fix H}\E\leq |H|. \] Todo isso implica que \(\gal \E{\fix H}=H\). O resto da afirmação 3. agora segue destas considerações.
Sejam \(G=\gal\E\F\) e \(H=\gal\E\K\). Seja \[ \fix H=\{\alpha\in\E\mid \sigma(\alpha)=\alpha\mbox{ para todo }\sigma\in H\}. \] Afirmamos que para \(g\in G\), \(\fix {gHg^{-1}}=g(\fix H)\). De fato, se \(g(\alpha)\in g(\fix H)\) com algum \(\alpha\in \fix H\), e \(h\in H\), então \[ ghg^{-1}g(\alpha)=gh(\alpha)=g(\alpha). \] Logo \(g(\fix H)\subseteq \fix{gHg^{-1}}\). A outra inclusão pode ser verificada por argumento similar. Ora temos pelo Lema 106.7 que \(\K:\F\) é normal se e somente se \(\sigma(\K)=\K\) para todo \(\sigma\in\gal\E\F\) que vale se e somente se \(\sigma(\fix H)=\fix H\) que vale pela afirmação anterior é equivalente a \(\fix{\sigma H\sigma^{-1}}=\fix{H}\) (Teorema 106.2); essa última afirmação é equivalente a \(\sigma H\sigma^{-1}=H\) para todo \(\sigma\in G\) que ocorre se e somente se \(H\unlhd G\) (Exercício 92.1). Assuma que \(\K:\F\) é normal e seja \(r:\gal\E\F\to\gal\K\F\) a restrição para \(\K\) (usamos que \(\K:\F\) é normal e assim \(\sigma(\K)=\K\) para todo \(\sigma\in\gal\E\F\)). Em outras palavras, \(r(\sigma)=\sigma|_\K\) para todo \(\sigma\in\gal\E\F\). A aplicação \(r\) é um homomorfismo com núcleo \(\gal\E\K\). A sobrejetividade de \(r\) segue do Lema 106.4. Portanto, usando o Teorema de Isomorfismo (Teorema 92.1), obtemos que \[ \gal\K\F\cong \gal\E\F/\gal\E\K. \]
107.3 Exemplos
Exemplo 107.1 Revisitamos o Exemplo 106.4. Seja \(\E\) o corpo de decomposição do polinômio \(x^3-2\in\Q[x]\) e considere a extensão \(\E:\Q\). Esta extensão é normal. As raízes do polinômio são \(\sqrt[3]2\), \(\xi\sqrt[3]2\) e \(\xi^2\sqrt[3]2\) onde \(\xi=\exp(2\pi i/3)\) é uma terceira raíz da unidade. Como \(\E\) é gerado por estas raízes sobre \(\Q\), temos que \[ \E=\Q(\sqrt[3]2, \xi\sqrt[3]2,\xi^2\sqrt[3]2)=\Q(\sqrt[3]2, \xi). \] Além disso, \(m_{\sqrt[3]2}(x)=x^3-2\) e \(m_{\xi}(x)=x^2+x+1\) e temos que \[ \dim_\Q\E=\dim_\Q\Q(\sqrt[3]2)\cdot\dim_{\Q(\sqrt[3]2)}\E=3\cdot 2=6. \] Pelo Teorema 106.3, \(|\gal\E\F|=6\). Se \(\varphi\in\gal\E\Q\), então \(\varphi\) está determinado pelas imagens \(\varphi(\sqrt[3]2)\) e \(\varphi(\xi)\). Note que \(\sqrt[3]2\) e \(\xi\) são raízes dos polinômios irredutíveis \(x^3-2\) e \(x^2+x+1\) (respetivamente), então \(\varphi(\sqrt[3]2)\) e \(\varphi(\xi)\) precisam ser raízes do mesmo polinômio. Temos então que \[ \varphi(\sqrt[3]2)\in\{\sqrt[3]2,\xi\sqrt[3]2,\xi^2\sqrt[3]2\}\quad\mbox{e}\quad \varphi(\xi)\in\{\xi,\xi^2\}. \] Isso dá seis possibilidades para o automorfismo \(\varphi\) e como já deduzimos que \(|\gal\E\Q|=6\), todas destas possibilidades precisam resultar em um elemento de \(\gal\E\F\). Na verdade, todo elemento de \(\gal\E\F\) induz uma permutação do conjunto \(R=\{\sqrt[3]2, \xi\sqrt[3]2,\xi^2\sqrt[3]2\}\) das raízes do polinômio \(x^3-2\) e convêm considerar \(\gal\E\Q\) como um grupo de permutações de \(R\). Como \(|R|=3\), toda permutação das três raízes resulta em um elemento de \(\gal\E\F\). Em particular \(\gal\E\F\cong\mbox{Sym}\,R\cong S_3\).
Na seguinte tabela, nós apresentamos explicitamente a correspondência entre os subgrupos de \(\mbox{Sym}\,R\) e os subcorpos de \(\E\).
| Subgrupo | Subcorpo | Normal? |
|---|---|---|
| \(1\) | \(\E=\Q(\xi,\sqrt[3]2)\) | Sim |
| \(\left<(\sqrt[3]2,\xi\sqrt[3]2)\right>\) | \(\Q(\xi^2\sqrt[3]2)\) | Não |
| \(\left<(\sqrt[3]2,\xi^2\sqrt[3]2)\right>\) | \(\Q(\xi\sqrt[3]2)\) | Não |
| \(\left<(\xi\sqrt[3]2,\xi^2\sqrt[3]2)\right>\) | \(\Q(\sqrt[3]2)\) | Não |
| \(\left<(\sqrt[3]2,\xi\sqrt[3]2,\xi^2\sqrt[3]2)\right>\) | \(\Q(\xi)\) | Sim |
| \(S_3\) | \(\Q\) | Sim |
Nós podemos ilustrar a posição destes corpos e grupo no seguinte desenho. 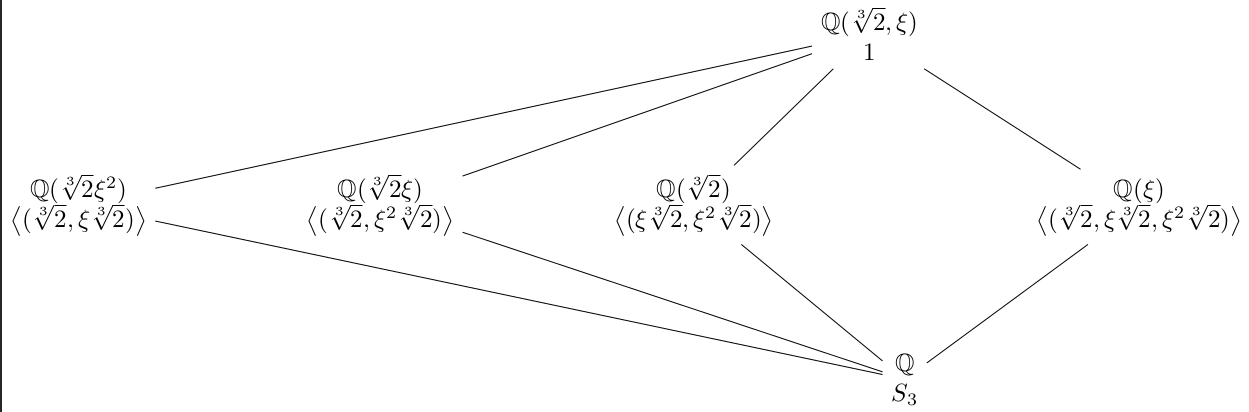
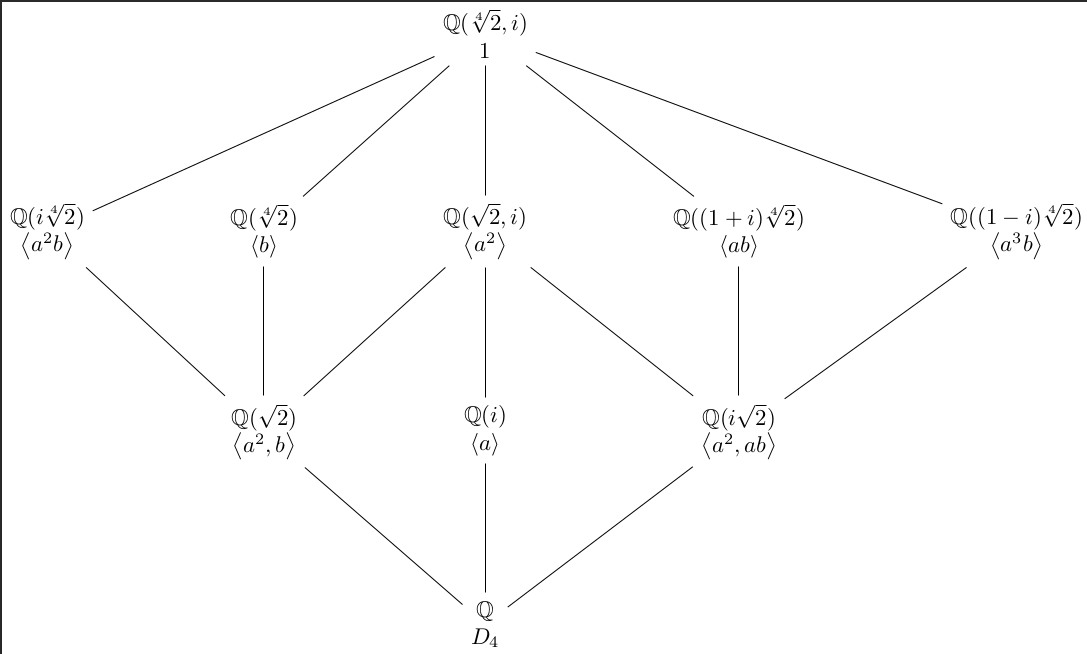
Exemplo 107.2 Considere o corpo de decomposição \(\E\) do polinômio \(x^4-2\) sobre \(\Q\). Similarmente ao exemplo anterior, temos que \[ \E=\Q(\sqrt[4]2,i) \] e \[ \dim_\Q\E=\dim_\Q\Q(\sqrt[4]2)\cdot\dim_{\Q(\sqrt[4]2)}\E=4\cdot 2=8 \] que implica que \(|\gal\E\Q|=8\). Além disso, um elemento \(\varphi\in\gal\E\Q\) é determinado pelas imagens \[ \varphi(\sqrt[4]2)\in\{\sqrt[4]2,-\sqrt[4]2,i\sqrt[4]2,-i\sqrt[4]2\}\quad\mbox{e}\quad \varphi(i)\in\{i,-i\}. \] Há oito opções na linha anterior, e o fato que \(|\gal\E\Q|=8\) implica que todas destas opções resultam em um automorfismo de \(\gal\E\Q\). Como no exemplo anterior, convêm considerar os elementos de \(\gal\E\Q\) como permutações do conjunto \(R=\{\sqrt[4]2,-\sqrt[4]2,i\sqrt[4]2,-i\sqrt[4]2\}\) das raízes de \(x^4-2\). Os automorfismos \[ \varphi_1:\sqrt[4]2\mapsto i\sqrt[4]2,\ i\mapsto i\quad\mbox{e}\quad\varphi_2:\sqrt[4]2\mapsto \sqrt[4]2,\ i\mapsto -i \] correspondem às permutações \[ a=(\sqrt[4]2,i\sqrt[4]2,-\sqrt[4]2,-i\sqrt[4]2)\quad\mbox{e}\quad b=(i\sqrt[4]2,-i\sqrt[4]2) \] e estas duas permutações geram um subgrupo de \(S_4\) isomorfo a \(D_4\).
Na seguinte tabela, nós apresentamos explicitamente a correspondência entre os subgrupos de \(\mbox{Sym}\,R\) e os subcorpos de \(\E\).
| Subgrupo | Subcorpo | Normal? |
|---|---|---|
| \(1\) | \(\E=\Q(\sqrt[4]2,i)\) | Sim |
| \(\left<b\right>\) | \(\Q(\sqrt[4]2)\) | Não |
| \(\left<a^2b\right>\) | \(\Q(i\sqrt[4]2)\) | Não |
| \(\left<a^2\right>\) | \(\Q(\sqrt 2,i)\) | Sim |
| \(\left<ab\right>\) | \(\Q((1+i)\sqrt[4]2)\) | Não |
| \(\left<a^3b\right>\) | \(\Q((1-i)\sqrt[4]2)\) | Não |
| \(\left<a^2,b\right>\) | \(\Q(\sqrt 2)\) | Sim |
| \(\left<a\right>\) | \(\Q(i)\) | Sim |
| \(\left<a^2,ab\right>\) | \(\Q(i\sqrt 2)\) | Sim |
| \(D_4\) | \(\Q\) | Sim |
O reticulado destes corpos está ilustrado no seguinte desenho.