39 Combinações lineares e geradores

39.1 Combinações lineares

Se lembre que nossos espaços vetoriais são sobre \(\R\).

Definição 39.1 Sejam \(\ul{v_1},\ldots,\ul{v_n}\) elementos do espaço vetorial \(V\). Uma combinação linear de \(\ul{v_1}, \ldots, \ul{v_n}\) é um elemento de \(V\) da forma \[\lambda_1\ul{v_1} + \cdots + \lambda_n\ul{v_n},\] com \(\lambda_1,\ldots,\lambda_n\) elementos de \(\R\).

Teorema 39.1 Seja \(X\) um conjunto de elementos do espaço vetorial \(V\). Então o conjunto \[W = \left\{\lambda_1\ul{v_1} + \cdots + \lambda_n\ul{v_n}\,|\,n\in \N\,,\,\lambda_1,\ldots,\lambda_n\in \R\,,\, \ul{v_1},\ldots,\ul{v_n}\in X\right\}\] de todas as combinações lineares (finitas!) de elementos de \(X\) é um subespaço de \(V\). Diremos que \(W\) é gerado por \(X\) e que os elementos de \(X\) são geradores de \(W\).

Vamos às vezes usar a notação \([X]\) para denotar o subespaço de \(V\) gerado por \(X\).

Comprovação. Proof. Exercício! É fácil mas muito importante. ◻

Exemplo 39.1

Considere o seguinte subconjunto de \(M_{2,3}(\R)\): \[X = \left\{ \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1\end{pmatrix}\,,\, \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix}\,,\, \begin{pmatrix} 0 & 0 & 2 \\ 0 & 1 & 0 \end{pmatrix} \right\}.\] Uma combinação linear geral de elementos de \(X\) tem a forma \[a\begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix} + b\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix}+ c\begin{pmatrix} 0 & 0 & 2 \\ 0 & 1 & 0 \end{pmatrix} = \begin{pmatrix} a & b & 2c \\ 0 & c & a \end{pmatrix},\] então o subespaço de \(M_{2,3}(\R)\) gerado por \(X\) é \[\left\{\left. \begin{pmatrix} a & b & 2c \\ 0 & c & a \end{pmatrix}\,\right|\, a,b,c\in \R \right\}.\]
Seja \(\R[x]\) o conjunto \[\{ a_nx^n + a_{n-1}x^{n-1} + \cdots + a_1x + a_0\,|\,n\in \N, a_0,\ldots,a_n\in \R\}\] dos polinômios com coeficientes em \(\R\). Afirmamos que \(\R[x]\) é um espaço vetorial (sobre \(\R\)). Para verificar esta afirmação, vamos definir a soma e o produto por escalar para polinômios.

SOMA: Pegue dois polinômios \(f(x), g(x)\). Já que uns coeficientes poderiam ser \(0\), podemos escrevê-las como: \[f(x) = a_nx^n + \cdots + a_1x + a_0\] \[g(x) = b_nx^n + \cdots + b_1x + b_0.\] onde o graus de \(f,g\) são no máximo \(n\). A soma de \(f\) e \(g\) é \[\begin{aligned} f(x) + g(x) & = (a_nx^n + \cdots + a_1x + a_0) + (b_nx^n + \cdots + b_1x + b_0) \\ & = (a_n+b_n)x^n + \cdots + (a_1+b_1)x + (a_0+b_0) \in \R[x] \end{aligned}\]

MÚLTIPLO ESCALAR: Dado \(f(x) = a_nx^n + \cdots + a_1x + a_0 \in \R[x]\) e \(\lambda\in \R\), temos \[\begin{aligned} \lambda\cdot f(x) & = \lambda(a_nx^n + \cdots + a_1x + a_0) \\ & = \lambda a_nx^n + \cdots + \lambda a_1x + \lambda a_0 \in \R[x]. \end{aligned}\] É fácil verificar que esta soma e produto escalar satisfazem as propriedades exigidas na definição de espaços vetoriais e portanto o conjunto \(\R[x]\) é um espaço vetorial.

Note que todo polinômio \(f(x)\in\R[x]\) determina uma função polinomial, nomeadamente, a função \[f\colon \R\to \R,\quad \alpha\mapsto f(\alpha),\] e polinômios distintos definem funções distintas (esta afirmação não é totalmente óbvia e você deve pensar em uma justificativa). Além disso a soma e o produto por escalar de polinômios correspondem à soma e ao produto escalar de funções. Considerando \(\R[x]\) como o conjunto de funções polinomiais, \(\R[x]\) pode ser visto como um subespaço do espaço de funções \(\mathcal F(\R,\R)\).

Considere o seguinte conjunto dos polinomios mais fáceis: \[X = \{1, x, x^2, x^3, \ldots\}.\] Observe que qualquer elemento \[f(x) = a_nx^n + a_{n-1}x^{n-1} + \cdots + a_1x + a_0\cdot 1\] de \(\R[x]\) é uma combinação linear dos elementos de \(X\), e que toda combinação linear de elementos de \(X\) é um elemento de \(\R[x]\). Então, \(\R[x]\) é gerado pelo conjunto \(X\).

Interseções e somas de subespaços

Sejam \(V\) um espaço vetorial e \(W,Y\) dois subespaços de \(V\).

A interseção \(W\cap Y\) de \(W\) e \(Y\) é mais um subespaço de \(V\).

Comprovação. Proof. Temos que confirmar que as propriedades de subespaço estão satisfeitas. Primeiro, \(\ul{0}\in W\) e \(\ul{0}\in Y\), logo \(\ul{0}\in W\cap Y\), mostrando que \(W\cap Y\neq\varnothing\).

Sejam \(\ul{u}, \ul{v}\in W\cap Y\). Então
- \(\ul{u}, \ul{v}\in W\) e \(W\) é subespaço, logo \(\ul{u}+\ul{v}\in W\),
- \(\ul{u}, \ul{v}\in Y\) e \(Y\) é subespaço, logo \(\ul{u}+\ul{v}\in Y\).
Segue que \(\ul{u} + \ul{v} \in W\cap Y\).
Exercício! A ideia é similar à primeira parte.

◻

Noutro lado, a união de dois subespaços de \(V\) geralmente não é um subespaço. Por exemplo, considere os seguintes subespaços de \(\R^2\): \[X = \{(x,0)\,|\, x\in \R\}\,,\quad Y = \{(0,y)\,|\,y\in \R\}\] (informalmente, \(X\) é o “eixo \(x\)” e \(Y\) é o “eixo \(y\)”). Os elementos \[(1,0)\,,\, (0,1)\in X\cup Y,\] mas \((1,0) + (0,1) = (1,1)\) não pertence nem a \(X\) nem a \(Y\), logo \((1,1)\not\in X\cup Y\):

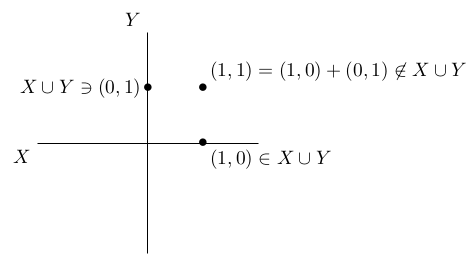
O jeito correto para “juntar” dois subespaços é o seguinte:

Definição 39.2 Sejam \(W,Y\) dois subespaços do espaço vetorial \(V\). A soma de \(W\) e \(Y\) é \[W + Y := \{\ul{w} + \ul{y}\,|\,\ul{w}\in W\,,\, \ul{y}\in Y\}.\]

Exercício 39.1 Confirme que \(W+Y\) é sempre um subespaço de \(V\).

Exemplo 39.2 Seja \(V = \R^3\) e considere os subespaços \[W = \{(x,y,0)\,|\,x, y\in \R\}\,,\quad Y = \{(0,y,z)\,|\,y,z\in \R\}.\] O subespaço \(W + Y\) é o próprio \(V\): dado \(\ul{v} = (x,y,z)\in V\), podemos escrever \[(x,y,z) = (x,y,0) + (0,0,z) \in W + Y.\]

Observe que esta soma não foi muito “eficiente”, no sentido que para obter \(V\) como soma, a gente podia ter usada subespaços menores. Por exemplo, pega \[Y' = \{(0,0,z)\,|\,z\in \R\} \subsetneq Y.\] Ainda temos \[W + Y' = \{(x,y,0) + (0,0,z)\,|\,x,y,z\in \R\} = \{(x,y,z)\,|\,x,y,z\in \R\} = \R^3.\] Temos \[W\cap Y = \{(0,y,0)\,|\,y\in \R\},\] enquanto \[W\cap Y' = \{\ul{0}\}.\] A não eficiencia de \(W+Y\) surge do fato que \(W\cap Y\neq \{\ul{0}\}\). Damos nome especial para somas eficientes:

Definição 39.3 Sejam \(W,Y\) subespaços de \(V\). Diremos que \(V\) é a soma direta de \(W\) e \(Y\) se

\(W+Y = V,\)
\(W\cap Y = \{\ul{0}\}\).

Neste caso, escrevemos \(V = W\oplus Y\).

Uma propriedade útil das somas diretas:

Sejam \(W,Y\) subespaços de algum espaço vetorial e \(V = W+Y\). Então \(V = W\oplus Y\) se, e somente se, cada elemento de \(V\) pode ser escrito unicamente como \(\ul{w}+\ul{y}\), com \(\ul{w}\in W, \ul{y}\in Y\).

Comprovação. Proof. Temos duas coisas para mostrar:

\(W\cap Y = \{\ul{0}\}\implies\)todo elemento pode ser escrito únicamente:

Suponha que algum \(\ul{v}\in V\) pode ser escrito como \(\ul{w} + \ul{y}\) E como \(\ul{w}' + \ul{y}'\) (com \(\ul{w}, \ul{w}'\in W, \ul{y}, \ul{y}'\in Y\)). Para mostrar unicidade da expressão, temos que confirmar que \(\ul{w}=\ul{w}'\) e \(\ul{y}=\ul{y}'\). Temos \[\ul{w}+\ul{y} = \ul{v} = \ul{w}' + \ul{y}' \implies \ul{w}-\ul{w}' = \ul{y}'-\ul{y} \in W\cap Y.\] Mas \(W\cap Y = \{\ul{0}\}\), então \(\ul{w} - \ul{w}' = \ul{0}\), logo \(\ul{w}=\ul{w}'\), e similarmente \(\ul{y}=\ul{y}'\).
todo elemento pode ser escrito únicamente\(\implies W\cap Y = \{\ul{0}\}\):

Pegue \(\ul{v}\in W\cap Y\), logo \(-\ul{v}\in W\cap Y\) já que \(W\cap Y\) é subespaço. Em particular, \(\ul{v}\in W\) e \(-\ul{v}\in Y\), e assim \[\ul{0} = \ul{0} + \ul{0} = \ul{v} - \ul{v}\] são duas expressões de \(\ul{0}\) como soma de alguém em \(W\) mais alguém em \(Y\). Já que todo elemento pode ser escrito unicamente assim, segue que \(\ul{v} = \ul{0}\). Mas \(\ul{v}\in W\cap Y\) foi arbitrário, então \(W\cap Y = \{\ul{0}\}\).

◻

Exemplo 39.3 Seja \(\mathcal{P}_2\) o subespaço de \(\R[x]\) gerado pelo conjunto \(\{1,x,x^2\}\). Então, \(\mathcal{P}_2\) é o conjunto dos polinômios da forma \(ax^2 + bx + c\) (\(a,b,c\in \R\)). Considere os subespaços \[D = \{ax^2 + ax + a\,|\,a\in \R\}\,,\quad E = \{bx + c\,|\, b,c\in \R\}.\] Vamos mostrar que \(\mathcal{P}_2 = D\oplus E\). Seja \(\alpha x^2 + \beta x + \gamma\) um elemento qualquer de \(\mathcal{P}_2\). Vamos tentar expressar este elemento como um elemento de \(D+E\): \[\alpha x^2 + \beta x + \gamma = (ax^2 + ax + a) + (bx + c) = ax^2 + (a+b)x + (a+c).\] Obtemos que \[\begin{aligned} \alpha & = a. \\ \beta & = a+b = \alpha + b \implies b = \beta - \alpha. \\ \gamma & = a+c = \alpha + c \implies c = \gamma - \alpha. \end{aligned}\] Seguem duas coisas:

todo elemento de \(\mathcal{P}_2\) pode ser escrito como soma de um elemento de \(D\) e um elemento de \(E\), logo \(\mathcal{P}_2 = D + E\).
essa expressão é única (\(a=\alpha\,,\, b = \beta - \alpha\,,\, c = \gamma - \alpha\), não temos escolha).

Segue pela proposição então que \(\mathcal{P}_2 = D \oplus E\).

Dependência Linear

Definição 39.4 O conjunto \(X\) de vetores no espaço vetorial \(V\) é linearmente dependente (LD) se existem \(\ul{v_1},\ldots,\ul{v_n}\in X\) e \(\lambda_1,\ldots,\lambda_n\in \R\), nem todos \(0\), tais que \[\lambda_1\ul{v_1} + \cdots + \lambda_n\ul{v_n} = \ul{0}.\] Se \(X\) não é linearmente dependente, então \(X\) é linearmente independente (LI). Logo \(X\) é LI se dados \(\ul{v_1}, \ldots,\ul{v_n}\in X\), \[\lambda_1\ul{v_1} + \cdots + \lambda_n\ul{v_n} = \ul{0}\,\,\implies\,\, \lambda_i = 0\,\,\forall i\in \{1,\ldots,n\}.\]

Exemplo 39.4

Seja \(\ul{v}\neq \ul{0}\) um vetor. Então \(X = \{\ul{v}\}\) é LI, pois a equação \[\lambda\ul{v} = \ul{0}\] está satisfeita somente quando \(\lambda = 0\).
Qualquer conjunto \(X\) que contém o vetor \(\ul{0}\) é LD, pois \[1\cdot \ul{0} = \ul{0}\quad\hbox{mas}\quad 1\neq 0.\]
O subconjunto \(\{(1,1), (1,-1)\}\subseteq \R^2\) é LI: suponha que \[\lambda (1,1) + \mu(1,-1) = \ul{0}.\] Temos que confirmar que \(\lambda = \mu = 0\). Mas \[\lambda (1,1) + \mu(1,-1) = (\lambda + \mu, \lambda - \mu) = (0,0).\] O segundo componente diz que \(\lambda - \mu = 0\), então \(\lambda = \mu\). O primeiro componente diz que \(0 = \lambda + \mu = \lambda + \lambda = 2\lambda\), então \(\lambda = \mu = 0\), logo \(\{(1,1),(1,-1)\}\) é LI.
Exercício: Sejam \(\ul{u}, \ul{v}\) vetores não nulos. Mostre que \(\{\ul{u}, \ul{v}\}\) é LD se, e somente se, \(\ul{u}\) é múltiplo escalar de \(\ul{v}\).
Sejam \(V = \R^3\) e \[X = \left\{ (1,2,5)\,,\, (7,-1,5)\,,\,(1,-1,-1)\right\}.\] Para ver se \(X\) é LD ou LI, temos que decidir se a equação \[x_1 (1,2,5) + x_2 (7,-1,5) + x_3 (1,-1,-1) = (0,0,0)\] possui solução não trivial ou não. A matriz do sistema linear correspondente é \[\begin{pmatrix}%[ccc|c] 1 & 7 & 1 & 0 \\ 2 & -1 & -1 & 0 \\ 5 & 5 & -1 & 0 \end{pmatrix}\] cuja forma escalonada reduzida é \[\begin{pmatrix}%[ccc|c] 1 & 0 & -2/5 & 0 \\ 0 & 1 & 1/5 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}.\] A terceira coluna não possui pivô, então \(x_3\) é livre. Em particular, o sistema possui soluções não triviais. Segue da definição que \(X\) é linearmente dependente.

Um subconjunto \(X\) é LD se existir uma dependência linear entre os elementos de \(X\). Mais precisamente:

Seja \(X\) um subconjunto de \(V\) com pelo menos dois elementos. Então \(X\) é LD se, e somente se, pelo menos um dos vetores \(\ul{v}\) de \(X\) pode ser escrito como combinação linear dos outros.

Comprovação. Proof. Exercício. Dicas:

Suponha que \(X\) é LD. Então existem \(\ul{v_1}, \ldots,\ul{v_n}\in X\) tais que \[\lambda_1\ul{v_1} + \cdots + \lambda_n\ul{v_n} = \ul{0}\] com nem todo \(\lambda_i = 0\). Pegue um \(\ul{v_i}\) com \(\lambda_i\neq 0\). Isole ele de um lado para expressar ele como combinação linear dos outros.
Expresse algum \(\ul{v}\in X\) como combinação linear de outros vetores em \(X\). Rearrange.

◻