47 Produtos internos e formas bilineares

47.1 Produtos internos

Nossos espaços vetoriais têm mais estrutura do que a gente está usando. Em $\R^2$ por exemplo aqui são duas bases diferentes:

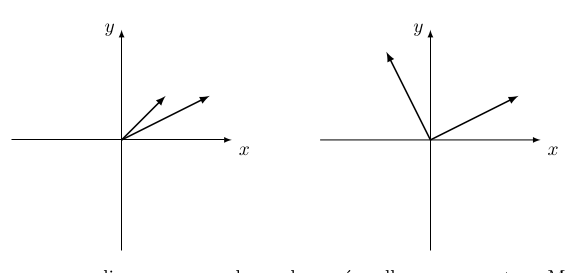
Até agora, não temos como dizer que uma dessas bases é melhor que a outra. Mas, esteticamente pelo menos, a segunda base parece mais legal, pois:

Os comprimentos dos dois vetores da segunda base são iguais,
O ângulo entre os vetores da segunda base é $90^{\tn{o}}$.

Vamos ver que de fato, na prática, a segunda base é bem mais útil do que a primeira. O conceito que estamos faltando para distinguir entre as duas é o produto interno.

Sejam $V,W$ dois espaços vetoriais. Se lembre que o produto cartesiano $V\times W$ é o conjunto dos pares \[V\times W = \{(\ul{v},\ul{w})\,|\,\ul{v}\in V,\,\ul{w}\in W\}.\]

Definição 47.1

Seja $V$ um espaço vetorial. Um produto interno sobre $V$ é uma função \[\begin{aligned} \langle-,-\rangle : V\times V & \to \,\,\,\,\R \\ (\ul{u},\ul{v}) & \mapsto \langle\ul{u},\ul{v}\rangle \end{aligned}\]

que satisfaz as seguintes propriedades:

(SIM): $\langle \ul{u},\ul{v}\rangle = \langle \ul{v},\ul{u}\rangle\quad\forall\,\ul{u},\ul{v}\in V$,
(LIN1): $\langle \ul{u},\ul{v}+\ul{w}\rangle = \langle \ul{u},\ul{v}\rangle + \langle \ul{u},\ul{w}\rangle\quad\forall \ul{u},\ul{v},\ul{w}\in V$,
(LIN2): $\langle \ul{u},\lambda\ul{v}\rangle = \lambda\langle \ul{u},\ul{v}\rangle\quad \forall \lambda\in \R, \forall \ul{u},\ul{v}\in V$.
(PD1): $\langle \ul{v},\ul{v}\rangle \geqslant 0\,\forall \ul{v}\in V$
(PD2): $\langle \ul{v},\ul{v}\rangle = 0\Longleftrightarrow \ul{v} = \ul{0}$.

Condição SIM diz que um produto interno é simétrico, pelas condições LIN1–LIN2, ele é linear no segundo componente (a gente vai ver que vai ser linear também no primeiro componente também), e finalmente as condições PD1–PD2 dizem que um produto interno é positivo definido.

Exemplo 47.1 O exemplo mais comum. Seja $V = \R^n$ e considere o produto conhecido de GAAL: Dados \[\ul{u} = (a_1,a_2,\ldots,a_n)\quad,\quad \ul{v} = (b_1,b_2,\ldots,b_n),\] então \[\langle \ul{u},\ul{v}\rangle = \ul{u}\cdot \ul{v} = a_1b_1 + a_2b_2 + \cdots + a_nb_n = \sum_{i=1}^n a_ib_i.\] Tratando vetores de $\R^n$ como matrizes colunas, $\ul{u}\cdot \ul{v}$ pode ser interpretado como produto de matrizes: \[\ul{u}\cdot \ul{v} = \ul{u}^t\ul{v} = \begin{pmatrix} a_1 & \cdots & a_n \end{pmatrix} \begin{pmatrix} b_1 \\ \vdots \\ b_n \end{pmatrix}.\]

Afirmo que este produto satisfaz todas as propriedades da definição. Vamos confirmar, então sejam \[\ul{u} = (a_1,\ldots,a_n),\quad \ul{v} = (b_1,\ldots,b_n),\quad \ul{w} = (c_1,\ldots,c_n)\] vetores em $\R^n$ e $\lambda\in \R$:

$\ul{u}\cdot \ul{v} = \sum_{i=1}^n a_ib_i = \sum_{i=1}^n b_ia_i = \ul{v}\cdot \ul{u}\quad\checkmark$
\[\begin{aligned} \ul{u}\cdot (\ul{v}+\ul{w}) & = (a_1,\ldots,a_n)\cdot (b_1+c_1,\ldots,b_n+c_n) \\ & = \sum_{i=1}^n a_i(b_i+c_i) \\ & = \sum_{i=1}^n a_ib_i + a_ic_i \\ & = \sum_{i=1}^n a_ib_i + \sum_{i=1}^n a_ic_i \\ & = \ul{u}\cdot \ul{v} + \ul{u}\cdot \ul{w}. \end{aligned}\]
Exercício.
$\ul{v}\cdot \ul{v} = \sum_{i=1}^n b_ib_i = \sum_{i=1}^n {b_i}^2 \geqslant 0$.
$0 = \ul{v}\cdot \ul{v} = \sum_{i=1}^n {b_i}^2 \implies b_i = 0\,\forall i\implies \ul{v} = \ul{0}$.

Então, o produto acima é um produto interno.

Na definiçao de produto interno, focamos no segundo componente. Mas, já que o produto é simétrico, as mesmas propriedades valem no primeiro componente:

Proposição 47.1 Seja $\langle-,-\rangle:V\times V \to \R$ um produto interno. Então

(LIN1’) $\langle \ul{u}+\ul{v},\ul{w}\rangle = \langle \ul{u},\ul{w}\rangle + \langle \ul{v},\ul{w}\rangle\quad \forall \ul{u},\ul{v},\ul{w}\in V$,
(LIN2’) $\langle\lambda \ul{u},\ul{v}\rangle = \lambda\langle \ul{u},\ul{v}\rangle\quad\forall \lambda\in \R, \forall \ul{u},\ul{v}\in V$.

Comprovação.

Temos \[\begin{aligned} \langle \ul{u}+\ul{v},\ul{w}\rangle & = \langle\ul{w},\ul{u}+\ul{v}\rangle\qquad\qquad (\hbox{por \textit{SIM}}) \\ & = \langle\ul{w},\ul{u}\rangle + \langle \ul{w},\ul{v}\rangle\qquad (\hbox{por \textit{LIN1}}) \\ & = \langle\ul{u},\ul{w}\rangle + \langle \ul{v},\ul{w}\rangle\qquad (\hbox{por \textit{SIM}})\,\,\checkmark \end{aligned}\]
Exercício.

◻

47.2 Formas bilineares

As condições LIN1, LIN2, LIN1’, LIN2’ dizem que um produto interno é bilinear. Isto é:

Proposição 47.2

Fixa $\ul{u}_0\in V$. As funções \[\begin{aligned} \langle -,\ul{u}_0\rangle : V &\to\,\,\,\, \R \\ \ul{v}\, & \mapsto \langle \ul{v},\ul{u}_0\rangle \end{aligned} \begin{aligned} \langle \ul{u}_0,-\rangle : V &\to\,\,\,\, \R \\ \ul{v}\, & \mapsto \langle\ul{u}_0,\ul{v}\rangle \end{aligned}\]

são transformações lineares.

Comprovação.

\[\begin{aligned} \langle\ul{u}_0,-\rangle (\ul{v}+\ul{w}) & = \langle\ul{u}_0,\ul{v}+\ul{w}\rangle \\ & = \langle\ul{u}_0,\ul{v}\rangle + \langle\ul{u}_0,\ul{w}\rangle\qquad\qquad (\hbox{por \textit{LIN1}}) \\ & = \langle\ul{u}_0,-\rangle(\ul{v}) + \langle\ul{u}_0,-\rangle(\ul{w})\quad\checkmark \end{aligned}\] e similarmente \[\begin{aligned} \langle\ul{u}_0,-\rangle (\lambda\ul{v}) & = \langle\ul{u}_0,\lambda\ul{v}\rangle \\ & = \lambda\langle\ul{u}_0,\ul{v}\rangle\qquad\quad (\hbox{por \textit{LIN2}}) \\ & = \lambda\langle\ul{u}_0,-\rangle(\ul{v}).\quad\checkmark \end{aligned}\]

◻

Definição 47.2

Seja $V$ um espaço vetorial. Uma forma bilinear sobre $V$ é uma função \[\begin{aligned} \langle-,-\rangle : V\times V & \to \,\,\,\,\R \\ (\ul{u},\ul{v}) & \mapsto \langle\ul{u},\ul{v}\rangle \end{aligned}\]

que satisfaz as propriedades LIN1, e LIN2, LIN1’ e LIN2’. Uma forma bilinear é dita simétrica se ela satisfaz a propriedade SIM.

Pode-se dizer então que um produto interno sobre um espaço vetorial $V$ é uma forma bilinear simétrica que também é positiva definida.

Exemplo 47.2

Sejam $A$ uma matriz $n\times n$ e $V$ um espaço vetorial de dimensão $n$ com base $B = \{\ul{b_1},\ldots,\ul{b_n}\}$. Se lembre que para $v\in V$, $[v]_B$ denota o vetor (coluna) das coordenadas de $v$ na base $B$. A função $\langle-,-\rangle_A : V\times V \to \R$ dada por \[\langle \ul{u},\ul{v}\rangle_A = {[\ul{u}]_B}^tA[\ul{v}]_B\] é uma forma bilinear: \[\begin{aligned} \langle \ul{u},\ul{v}+\ul{w}\rangle_A & = {[\ul{u}]_B}^tA[\ul{v}+\ul{w}]_B \\ & = {[\ul{u}]_B}^tA([\ul{v}]_B+[\ul{w}]_B)\qquad \mbox{($v\mapsto [v]_B$ é linear)}\\ & = {[\ul{u}]_B}^tA[\ul{v}]_B + {[\ul{u}]_B}^tA[\ul{w}]_B \qquad (\hbox{propriedades de matrizes}) \\ & = \langle \ul{u},\ul{v}\rangle_A + \langle \ul{u},\ul{w}\rangle_A\qquad\checkmark \end{aligned}\] \[\begin{aligned} \langle \ul{u},\lambda\ul{v}\rangle_A & = {[\ul{u}]_B}^tA[\lambda\ul{v}]_B \\ & = {[\ul{u}]_B}^tA(\lambda[\ul{v}]_B)\qquad \mbox{($v\mapsto [v]_B$ é linear)}\\ & = {\lambda[\ul{u}]_B}^tA[\ul{v}]_B\qquad (\hbox{propriedades de matrizes}) \\ & = \lambda\langle \ul{u},\ul{v}\rangle_A\qquad\checkmark \end{aligned}\]

Exercício: Confirme que a função é linear no primeiro componente também.

47.3 Formas bilineares simétricas

Em geral, esta forma não vai ser simétrica. Por exemplo, pegue $A = \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}$, $\ul{u} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \ul{v} = \begin{pmatrix} 1 \\ 1 \end{pmatrix}$. Temos \[\langle\ul{u},\ul{v}\rangle_A = \ul{u}^tA\ul{v} = \begin{pmatrix} 1 & 0 \end{pmatrix}\begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}\begin{pmatrix} 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 \end{pmatrix}\begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \end{pmatrix} = \ul{\ul{1}}\] enquanto \[\langle\ul{v},\ul{u}\rangle_A = \ul{v}^tA\ul{u} = \begin{pmatrix} 1 & 1 \end{pmatrix}\begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}\begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 & 1 \end{pmatrix}\begin{pmatrix} 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \end{pmatrix} = \ul{\ul{0}}.\] De fato, temos o seguinte lema.

Lema 47.1 A forma bilinear $\langle-,-\rangle_A$ é simétrica se, e somente se, a matriz $A = (a_{ij})$ é simétrica (isto é, se $A = A^t$).

Comprovação. $A = A^t$. Pegue $\ul{u}, \ul{v}\in V$ quaisquer. Já que $[\ul{u}]_B^tA[\ul{v}]_B$ é uma matriz $1\times 1$, temos $[\ul{u}]_B^tA[\ul{v}]_B = ([\ul{u}]_B^tA[\ul{v}]_B)^t$. Agora \[\langle \ul{u},\ul{v}\rangle_A = [\ul{u}]_B^tA[\ul{v}]_B = ([\ul{u}]_B^tA[\ul{v}]_B)^t = [\ul{v}]_B^tA^t{[\ul{u}]_B^t}^t = [\ul{v}]_B^tA[\ul{u}]_B = \langle \ul{v},\ul{u}\rangle_A,\] mostrando que a forma é simétrica.

Suponha que a forma é simétrica. Tem-se que $[b_i]_B=\begin{pmatrix} 0 & \cdots & 1 & \cdots & 0 \end{pmatrix}$. Temos \[\langle \ul{b_i},\ul{b_j}\rangle_A = [\ul{b_i}]_B^tA[\ul{b_j}]_B = [\ul{b_i}]_B^t\begin{pmatrix} a_{1j} \\ a_{2j} \\ \vdots \\ a_{nj} \end{pmatrix} = a_{ij},\] enquanto \[\langle \ul{b_j},\ul{b_i}\rangle_A = [\ul{b_j}]_B^tA[\ul{b_i}]_B = [\ul{b_j}]_B^t\begin{pmatrix} a_{1i} \\ a_{2i} \\ \vdots \\ a_{ni} \end{pmatrix} = a_{ji}.\] Já que a forma é simétrica, obtemos que \[a_{ij} = \langle \ul{b_i},\ul{b_j}\rangle_A = \langle \ul{b_j},\ul{b_i}\rangle_A = a_{ji}\quad \forall\, i,j.\] Isto é, $A$ é simétrica. ◻

Então, no fim das contas, dada uma matriz simétrica $A$, a função $V\times V \to \R$ dada por $\langle \ul{u},\ul{v}\rangle_A = \ul{u}^tA\ul{v}$ é uma forma bilinear simétrica (pois satisfaz propriedades SIM, LIN1, LIN2, LIN1’, LIN2’ da definição).

47.4 Positividade de formas

Ainda temos que decidir quando esta forma é positiva definida. Vamos voltar para esta questão mais para frente. Por enquanto, seguem dois exemplos de matrizes simétricas cujas formas bilineares correspondentes são positivas definidas:

Exemplo 47.3

Sejam $V = \R^n$ e $A = I$, a matriz identidade. Neste caso, \[\langle\ul{u},\ul{v}\rangle_I = \ul{u}^tI\ul{v} = \ul{u}^t\ul{v} = \ul{u}\cdot \ul{v}.\] Então este produto interno é o produto escalar conhecido de GAAL. Já confirmamos que ele é positivo definido.
\[A = \begin{pmatrix} 2 & -1 \\ -1 & 2 \end{pmatrix}.\] Pegando $\ul{v} = \begin{pmatrix} x \\y \end{pmatrix}$ qualquer, temos \[\langle \ul{v},\ul{v}\rangle_A = \ul{v}^t\begin{pmatrix} 2 & -1 \\ -1 & 2 \end{pmatrix}\ul{v} = \begin{pmatrix} x & y \end{pmatrix}\begin{pmatrix} 2 & -1 \\ -1 & 2 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} = 2x^2 - 2xy + 2y^2.\] Mas observe que \[2x^2 - 2xy + 2y^2 = (x^2 - 2xy + y^2) + x^2 + y^2 = (x-y)^2 + x^2 + y^2.\] Já que este valor é uma soma de números quadrados, segue que
- ele é $\geqslant 0$ para quaisquer valores $x,y$,
- ele é $0$ se, e somente se, todos os termos são $0$. Ou seja se, e somente se, $x=y=0$.
Concluímos que $\langle-,-\rangle_A$ é um produto interno (sendo simétrico e positivo definido).

Nesta disciplina, vamos ter interesse principalmente em produtos internos, mas nas diversas áreas da matemática, as formas bilineares também exercem um papel importante.

Seguem várias utilidades e aplicações dos produtos internos.

47.5 Norma e distância

Um espaço vetorial $V$, junto com um produto interno \[V\times V\to \R\] será chamado de espaço vetorial com produto interno.

Definição 47.3 Seja $V$ um espaço vetorial com produto interno $\langle-,-\rangle$. A norma do vetor $\ul{v}\in V$ é o número \[\|\ul{v}\| = \sqrt{\langle\ul{v},\ul{v}\rangle}.\]

A norma de um vetor representa o comprimento dele.

Exemplo 47.4 A norma de um vetor com respeito ao produto escalar normal de $\R^n$ é simplesmente o comprimento do segmento que representa o vetor. Por exemplo, em $\R^2$, a norma do vetor $\ul{v} = (x,y)$ é \[\|\ul{v}\| = \sqrt{(x,y)\cdot (x,y)} = \sqrt{x^2 + y^2},\] que é, pelo teorema de Pitágoras, o comprimento do segmento que representa $\ul{v}$:

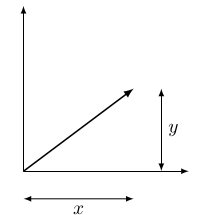
Então, por exemplo $\|(3,4)\| = \sqrt{3^2 + 4^2} = 5$ com respeito ao produto escalar normal.

Mas a norma de um vetor depende do produto interno. Por exemplo, considere $\R^2$ com o produto interno $\langle -,-\rangle_A$ dada pela matriz \[A = \begin{pmatrix} 2 & -1 \\ -1 & 2 \end{pmatrix}.\] A norma de $(x,y)$ com respeito a este produto interno é \[\|(x,y)\| = \sqrt{\begin{pmatrix} x & y \end{pmatrix}\begin{pmatrix} 2 & -1 \\ -1 & 2 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}} = \sqrt{2(x^2 - xy + y^2)}.\] Por exemplo, \[\|(3,4)\| = \sqrt{2(3^2 - 3\cdot 4 + 4^2)} = \sqrt{26}\,\, (\neq 5).\]

A norma de um vetor não deve ser negativo e a norma de um vetor não nulo deve ser positiva. Isso é uma das razões para exigir que o produto interno seja positivo definido:

Proposição 47.3 Seja $V$ um espaço vetorial com produto interno.

$\|\ul{v}\|\geqslant 0\, \forall \ul{v}\in V$, e $\|\ul{v}\| = 0 \Longleftrightarrow \ul{v} = \ul{0}$,
Dado um escalar $\lambda\in \R$, $\|\lambda\ul{v}\| = |\lambda|\cdot \|\ul{v}\|$.

Comprovação.

Imediato, já que o produto interno é positivo definido.
$\|\lambda \ul{v}\| = \sqrt{\langle\lambda\ul{v},\lambda\ul{v}\rangle} = \sqrt{\lambda\langle \ul{v},\lambda\ul{v}\rangle} = \sqrt{\lambda^2\langle \ul{v},\ul{v}\rangle} = |\lambda|\sqrt{\langle\ul{v},\ul{v}\rangle} = |\lambda|\cdot \|\ul{v}\|$.

◻

Um vetor $\ul{v}$ num espaço vetorial com produto interno é unitário se $\|\ul{v}\| = 1$. Para qualquer vetor não nulo $\ul{v}$, $\|\ul{v}\|\neq 0$ e o vetor $\frac{1}{\|\ul{v}\|}\ul{v}$ é unitário: \[\left\|\frac{1}{\|\ul{v}\|}\ul{v}\right\| = \frac{1}{\|\ul{v}\|}\|\ul{v}\| = 1\quad\checkmark\] Diremos que o vetor unitário $\ul{v}/\|\ul{v}\|$ é a normalização do vetor $\ul{v}$, ou o vetor $\ul{v}$ normalizado.

47.6 A desigualdade de Cauchy-Schwarz

Umas propriedades mais sutis:

Proposição 47.4 Sejam $\ul{u}, \ul{v}$ dois vetores num espaço vetorial com produto interno. Então \[|\langle\ul{u},\ul{v}\rangle| \leqslant \|\ul{u}\|\cdot \|\ul{v}\|.\]

Comprovação.

A desigualdade é imediata se $\ul v=\ul 0$. (confirme!), então vamos supor que $\ul{v}\neq \ul{0}$. Para qualquer número $\lambda$, temos \[0\leqslant\|\ul{u} - \lambda\ul{v}\|^2 = \langle\ul{u}-\lambda\ul{v},\ul{u}-\lambda\ul{v}\rangle = \langle \ul{u},\ul{u}\rangle - 2\lambda\langle\ul{u},\ul{v}\rangle + \lambda^2\langle\ul{v},\ul{v}\rangle.\] Escolhemos um $\lambda$ espertamente. Pegue \[\lambda = \frac{\langle \ul{u},\ul{v}\rangle}{\|\ul{v}\|^2}.\] Obtemos \[\begin{aligned} 0 & \leqslant \langle \ul{u},\ul{u}\rangle - 2\lambda\langle\ul{u},\ul{v}\rangle + \lambda^2\langle\ul{v},\ul{v}\rangle \\ & = \|\ul{u}\|^2 - 2\lambda\langle\ul{u},\ul{v}\rangle + \lambda^2\|\ul{v}\|^2 \\ & = \|\ul{u}\|^2 - 2\frac{\langle\ul{u},\ul{v}\rangle^2}{\|\ul{v}\|^2} + \frac{\langle\ul{u},\ul{v}\rangle^2}{\|\ul{v}\|^2} \\ & = \|\ul{u}\|^2 - \frac{\langle\ul{u},\ul{v}\rangle^2}{\|\ul{v}\|^2}. \end{aligned}\]

Rearranjando, obtemos \[\langle\ul{u},\ul{v}\rangle^2 \leqslant \|\ul{u}\|^2\cdot \|\ul{v}\|^2,\] e finalmente pegando raiz quadradas, \[|\langle\ul{u},\ul{v}\rangle| \leqslant \|\ul{u}\|\cdot \|\ul{v}\|.\] ◻

Exemplo 47.5

Vamos pegar dois vetores $\ul{u} = (1,-4), \ul{v} = (2,3)$ de $\R^2$ com produto interno dado pela matriz \[A = \begin{pmatrix} 2 & -1 \\ -1 & 2 \end{pmatrix}\] e confirmar que a desigualdade está satisfeita. Temos \[|\langle\ul{u},\ul{v}\rangle| = \left|\begin{pmatrix} 1 & -4 \end{pmatrix}\begin{pmatrix} 2 & -1 \\ -1 & 2 \end{pmatrix}\begin{pmatrix} 2 \\ 3 \end{pmatrix}\right| = \left|\begin{pmatrix} 1 & -4 \end{pmatrix}\begin{pmatrix} 1 \\ 4 \end{pmatrix}\right| = |-15| = 15,\] enquanto \[\begin{aligned} \|\ul{u}\|\cdot\|\ul{v}\| & = \sqrt{\begin{pmatrix} 1 & -4 \end{pmatrix}\begin{pmatrix} 2 & -1 \\ -1 & 2 \end{pmatrix}\begin{pmatrix} 1 \\ -4 \end{pmatrix}}\cdot\sqrt{\begin{pmatrix} 2 & 3 \end{pmatrix}\begin{pmatrix} 2 & -1 \\ -1 & 2 \end{pmatrix}\begin{pmatrix} 2 \\ 3 \end{pmatrix}} \\ & = \sqrt{42}\cdot \sqrt{14} = 14\sqrt{3}\approx 24 \geqslant 15.\quad\checkmark \end{aligned}\]

47.7 A desigualdade triangular

Se lembre de GAAL que a soma de dois vetores $\ul{u} + \ul{v}$ em $\R^n$ pode ser visualizada por colocar um representante de $\ul{v}$ começando no ponto final de um representante de $\ul{u}$. O vetor $\ul{u}+\ul{v}$ tem representante começando no ponto inicial de $\ul{u}$ e indo pro ponto final de $\ul{v}$:

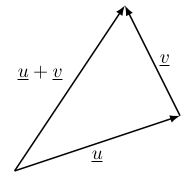
A desigualdade triangular diz que o comprimento de $\ul{u}+\ul{v}$ não pode ser maior do que a soma dos comprimentos de $\ul{u}$ e $\ul{v}$. De fato, esta desigualadae também vale em geral:

Proposição 47.5 Sejam $\ul{u}, \ul{v}$ dois vetores num espaço vetorial com produto interno. Então \[\|\ul{u}+\ul{v}\| \leqslant \|\ul{u}\| + \|\ul{v}\|.\]

Comprovação.

\[\|\ul{u}+\ul{v}\|^2 \leqslant \left(\|\ul{u}\| + \|\ul{v}\|\right)^2.\] Temos \[\begin{aligned} \|\ul{u}+\ul{v}\|^2 & = \langle \ul{u}+\ul{v},\ul{u}+\ul{v}\rangle \\ & = \langle \ul{u},\ul{u}\rangle + 2\langle \ul{u},\ul{v}\rangle + \langle \ul{v},\ul{v}\rangle \\ & = \|\ul{u}\|^2 + 2\langle \ul{u},\ul{v}\rangle + \|\ul{v}\|^2 \\ & \leqslant \|\ul{u}\|^2 + 2\|\ul{u}\|\cdot\|\ul{v}\| + \|\ul{v}\|^2 \qquad (\hbox{Cauchy-Schwarz}) \\ & = \left(\|\ul{u}\| + \|\ul{v}\|\right)^2.\qquad\checkmark \end{aligned}\]

◻

Mais uma definição. A distância entre dois vetores $\ul{u}, \ul{v}$ do espaço vetorial com produto interno $V$ é o número $\|\ul{u} - \ul{v}\|$. Por exemplo, a distância entre um vetor $\ul{u}$ e ele mesmo é \[\|\ul{u} - \ul{u}\| = \|\ul{0}\| = 0.\] A distância entre $\ul{u}$ e $-\ul{u}$ é \[\|\ul{u} - (-\ul{u})\| = \|2\ul{u}\| = 2\|\ul{u}\|.\]