\[ \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\R}{\mathbb R} \newcommand{\C}{\mathbb C} \newcommand{\F}{\mathbb F} \newcommand{\K}{\mathbb K} \newcommand{\L}{\mathbb L} \newcommand{\N}{\mathbb N} \newcommand{\sym}[1]{\operatorname{Sym}(#1)} \newcommand{\GLV}[1]{\operatorname{GL}(#1)} \newcommand{\SLV}[1]{\operatorname{SL}(#1)} \newcommand{\GL}[2]{\operatorname{GL}(#1,#2)} \newcommand{\SL}[2]{\operatorname{SL}(#1,#2)} \newcommand{\lxor}{\dot\lor} \newcommand{\cond}{\Rightarrow} \newcommand{\bicond}{\Leftrightarrow} \newcommand{\mdc}[2]{\operatorname{mdc}(#1,#2)} \newcommand{\grau}[1]{\operatorname{grau}(#1)} \newcommand{\real}[1]{\mathfrak R(#1)} \newcommand{\imag}[1]{\mathfrak I(#1)} \newcommand{\argz}[1]{\mbox{arg}(#1)} \DeclareMathOperator{\sen}{sen} \newcommand{\cis}[1]{\cos #1+i\sen #1} \newcommand{\E}{\mathbb E} \newcommand{\aut}[1]{\textrm{Aut}(#1)} \newcommand{\fix}[1]{\textrm{Fix}(#1)} \newcommand{\gal}[2]{\textrm{Gal}(#1:#2)} \newcommand{\overbar}[1]{\mkern 1.5mu\overline{\mkern-1.5mu#1\mkern-1.5mu}\mkern 1.5mu} \newcommand{\ul}[1]{\underline{#1}} \newcommand{\tn}[1]{\textnormal{#1}} \]
54 Computações com Python II
Vamos resolver alguns problemas numéricos usando as bibliotecas SymPy e NumPy da linguagem de programação Python.
54.1 Grafos e matrizes
Um grafo é uma coleção de vértices ligados com arestas. Por exemplo,
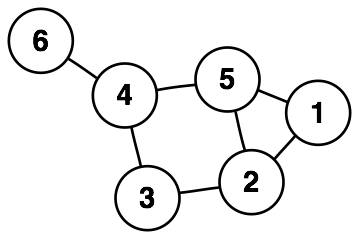
é um grafo. Nossos grafos serão não direcionados (ou seja, as arestas não são direcionadas), eles não terão arestas múltiplas ou laços (laço é uma aresta que tem o mesmo ponto inicial e ponto final). Este tipo de grafo chama-se grafo simples na literatura.
A matriz de adjecência de um grafo \(\Gamma\) é a matriz cujas linhas e colunas estão indexadas pelos vértices do grafo e a entrada na \(i\)-ésima linha e \(j\)-ésima coluna é \(1\) se \(v_i\) e \(v_j\) são adjacentes; caso contrário, a entrada é nula. Por exemplo, a matriz de adjacência do grafo \(\Gamma\) na imagem é a matriz \[ A(\Gamma)=\begin{pmatrix} 0 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \end{pmatrix}. \] A matriz de grau de um grafo é a matriz diagonal \(n\times n\) que contém o grau dos vértices (ou seja, o número de vizinhos) nas entradas diagonais. A matriz de grau do grafo \(\Gamma\) em cima é \[ G(\Gamma)=\begin{pmatrix} 2 & 0 & 0 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 & 0 \\ 0 & 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{pmatrix}. \] A laplaciana de um grafo \(\Gamma\) é a matriz \(G(\Gamma)-A(\Gamma)\). A laplaciana do grafo na imagem é \[ A(\Gamma)=\begin{pmatrix} 2 & -1 & 0 & 0 & -1 & 0 \\ -1 & 3 & -1 & 0 & -1 & 0 \\ 0 & -1 & 2 & -1 & 0 & 0 \\ 0 & 0 & -1 & 3 & -1 & -1 \\ -1 & -1 & 0 & -1 & 3 & 0 \\ 0 & 0 & 0 & -1 & 0 & 1 \end{pmatrix}. \]
Exercício 54.1 Escreva funções em Python para calcular as matrizes de adjacência, a matriz de grau e a laplaciana de um grafo. Assuma que o grafo está dado como uma lista de arestas na forma (i,j) indicando que \(v_i\) e \(v_j\) são adjacentes. Por exemplo o grafo na imagem pode ser definido com a lista
edge_list = [(0,1),(0,4),(1,2),(1,4),(2,3),(3,4),(3,5)]Note que os vértices estão indexados por 0,...,5 em vez de 1,...,6 seguindo as convenções da linguagem Python.
Para definir as matrizes do grafo, use o pacote SymPy como no Capítulo 47.
As funções podem aceitar um argumento adicional indicando o número de vértices do grafo; alternativamente, este número pode ser calculado também usando a lista de arestas, mas tenha cuidado, pois neste último caso o grafo não poderá ter vértices isolados.
A sua função deve funcinar na maneira seguinte.
edge_list = [(0,1),(0,4),(1,2),(1,4),(2,3),(3,4),(3,5)]
adjacency_matrix( 6, edge_list )
Matrix([
[0, 1, 0, 0, 1, 0],
[1, 0, 1, 0, 1, 0],
[0, 1, 0, 1, 0, 0],
[0, 0, 1, 0, 1, 1],
[1, 1, 0, 1, 0, 0],
[0, 0, 0, 1, 0, 0]])
degree_matrix( 6, edge_list )
Matrix([
[2, 0, 0, 0, 0, 0],
[0, 3, 0, 0, 0, 0],
[0, 0, 2, 0, 0, 0],
[0, 0, 0, 3, 0, 0],
[0, 0, 0, 0, 3, 0],
[0, 0, 0, 0, 0, 1]])
laplacian( 6, edge_list )
Matrix([
[ 2, -1, 0, 0, -1, 0],
[-1, 3, -1, 0, -1, 0],
[ 0, -1, 2, -1, 0, 0],
[ 0, 0, -1, 3, -1, -1],
[-1, -1, 0, -1, 3, 0],
[ 0, 0, 0, -1, 0, 1]])DICA: Para construir a matriz de adjacência, pode começar por construir uma matriz nula, usando a função Matrix.zeros. Depois use um laço for correndo sobre os elementos da lista de arestas. Para construir a matriz de grau, pode começar por construir a matriz de adjacência (chamando a função já escrita) e usar sum( m[i,:]) para calcular a soma da \(i\)-ésima linha.
Exercício 54.2 Construe as matrizes de adjacência dos grafos dados com as seguintes listas de arestas.
[(0, 4), (0, 10), (0, 17), (1, 7), (1, 8), (1, 10), (1, 11), (1, 13), (1, 14), (2, 8), (2, 16), (3, 10), (4, 7), (4, 14), (4, 19), (6, 18), (7, 9), (7, 15), (7, 18), (8, 19), (9, 13), (11, 16), (12, 15)][(0, 3), (0, 5), (0, 12), (0, 14), (1, 4), (1, 17), (1, 19), (2, 6), (2, 8), (2, 15), (2, 16), (3, 11), (3, 12), (3, 14), (3, 15), (4, 8), (4, 9), (4, 10), (4, 11), (4, 18), (5, 6), (5, 7), (5, 11), (5, 13), (6, 15), (6, 17), (7, 9), (7, 14), (7, 16), (8, 9), (10, 13), (10, 16), (11, 19), (12, 14), (12, 16), (12, 19), (13, 15), (14, 15), (14, 17), (15, 18)][(2, 4), (4, 16), (6, 7), (7, 10), (7, 14), (7, 15), (7, 16), (8, 10), (9, 14), (9, 18), (9, 19), (12, 18), (14, 16)]54.2 Autovalores dos grafos
Os autovalores das várias matrizes associados com um grafo tem relação com a estrutura do grafo.
Lema 54.1 Seja \(\Gamma\) um grafo e sejam \(A(\Gamma)\) e \(L(\Gamma)\) a sua matriz de adjacência e laplaciana. Temos que
- O número \(0\) é autovalor de \(L(\Gamma)\) e a sua multiplicidade (a dimensão do autoespaço) é igual ao número de componentes conexos do grafo.
- A entrada \((i,j)\) em \(A(\Gamma)^k\) é o número dos caminhos de comprimento \(k\) do vértice \(v_i\) até o vértice \(v_j\). Em particular, a entrada \((i,i)\) na diagonal de \(A(\Gamma)^k\) é o número de caminhnos fechados de comprimento \(k\) que começam e terminam no vértice \(v_i\).
- Consequentemente,
\[ \frac 16\mbox{Tr}(A^3)=\mbox{o número de triângulos em $\Gamma$.} \]
Exercício 54.3
- Calcule o número de componentes conexos dos grafos que apareceram no Exercício 54.1 calculando a multiplicidade do autovalor \(0\). Use a função
m.eigenvals(). - Calcule o número dos triângulos dos grafos no Exercício 54.1 calculando
- o traço de \(A^3\);
- a soma \(\sum_{i=1}^n\lambda_i^3\) onde \(\lambda_1,\ldots,\lambda_n\) são os autovalores. Explique porque os dois números são iguais.
- Escreva funções
nr_connected_components( nr_verts, edge_list )enr_triangles( nr_verts, edge_list )para calcular o número de componentes conexos e o número de triângulos de um grafo dado por lista de arestas.
DICA: Use m.eigenvals(). O output desta função é um dicionário na forma { v1: m1,...,vk: mk } onde os vi são os autovalores e mi é a sua multiplicade. Quando calcular a soma no item 2(b), vai ter calcular \(\lambda_i^3\) \(m_i\) vezes.
54.3 Calculando um autovetor
Um método usando na prática para calcular autovetores de uma matriz quadrada \(M\) de tamanho \(n\times n\) é o seguinte.
- Escolha um vetor coluna \(v\) de tamanho \(n\times 1\) não nula aleatoriamente.
- Ponha \[ v := \frac{M v}{\|M v\|}. \]
- Repita passo (2) até a diferença entre dois vetores em duas iterações seguidas é suficientemente pequena.
Exercício 54.4 Escreva uma função eigen_iter( m, v ) que, dados \(M\) e \(v\), executa o algoritmo descrito em cima. Escreva duas versões desta função. Na primeira, o usuário pode especificar o número de iterações feitas na computação, enquanto na segunda o usuário pode colocar um argumento epsilon e a computação para quando norma da diferença de dois vetores em duas iterações seguidas é menor ou igual a epsilon.
Neste exercício, use NumPy em vez de SymPy.
Você vai ter que transformar a sua matriz para array de NumPy. A sua função deve se comportar como no exemplo eigen_iter abaixo. Note que a função eigen_iter foi escrita para aceitar os argumentos nr_iter e epsilon opcionais que determinam o número de iterações ou o valor de epsilon. Você pode escrever duas funções separadas se assim for mais fácil.
import numpy as np
edge_list = [(0,1),(0,4),(1,2),(1,4),(2,3),(3,4),(3,5)]
m = adjacency_matrix( 6, edge_list )
m = np.array( m, dtype = float )
v = np.array( [1,0,0,0,0,0] )
eigen_iter( m, v, nr_iter = 5 )
array([0.47723999, 0.47723999, 0.35792999, 0.41758499, 0.47723999,
0.11931 ])
eigen_iter( m, v, nr_iter = 20 )
array([0.40105562, 0.50149968, 0.35920242, 0.40649925, 0.51716627,
0.16100772])
eigen_iter( m, v, nr_iter = 100 )
array([0.40109752, 0.50232899, 0.35830714, 0.40758615, 0.51625165,
0.16049961])
eigen_iter( m, v, epsilon = 0.1 )
array([0.37722842, 0.51868907, 0.35365164, 0.37722842, 0.54226585,
0.16503743])
eigen_iter( m, v, epsilon = 0.01 )
array([0.40122823, 0.50426669, 0.35618752, 0.41016543, 0.51405838,
0.15927888])
eigen_iter( m, v, epsilon = 0.001 )
array([0.40108736, 0.50212094, 0.35853196, 0.40731368, 0.5164812 ,
0.1606271 ])DICA: Para calcular a norma de um vetor (array), use np.linalg.norm. Em NumPy, o produto de matrizes está escrito com A@B.
Exercício 54.5 Calcule um autovalor e um autovetor para as matrizes de adjacência e matrizes laplacianas calculadas no Exercício 54.1.