38 Espaços vetoriais

38.1 Introdução

Álgebra Linear 1 é uma continuação de GAAL. Em GAAL, estudamos propriedades de:

Matrizes com entradas em \(\R\)
Vetores (geralmente em \(\R^2\) ou \(\R^3\))

Em Álgebra Linear 1 vamos re-estudar os conceitos de vetor e matriz. Umas ideias principais:

Um espaço vetorial \(V\) será uma coleção de todos os vetores de um dado tipo (por exemplo, \(\R^2, \R^3\) são espaços vetoriais). Vamos considerar espaços do tipo \(\R^n\) com \(n\) maior, e até espaços com “\(n=\infty\)”.
Uma matriz será considerada como um tipo de aplicação especial entre espaços vetoriais. Tais aplicações se chamam transformações lineares. Por exemplo, uma matriz \(3\times 2\) vai ser uma transformação linear de \(\R^2\) a \(\R^3\).

Com essas ideias em mão, várias definições peculiares de GAAL se tornam mais naturais. Por exemplo, suponha que temos transformações lineares assim: \[\R^4 \xleftarrow{g} \R^3 \xleftarrow{f} \R^2.\]

\(f\) corresponde a uma matriz \(3\times 2\) \(A\),
\(g\) corresponde a uma matriz \(4\times 3\) \(B\).

A composição \(gf\) é uma transformação linear de \(\R^2\) a \(\R^4\) , logo corresponde a uma matriz \(4\times 2\). Qual?

Resposta: a matriz da composição será o PRODUTO \(BA\) das matrizes \(B\) e \(A\). Por isso o produto de matrizes é definido assim.

38.2 Introdução aos números Complexos

Neste curso, nossa tarefa principal será para estudar os espaços vetoriais com coeficientes em \(\R\) (os espaços \(\R^2, \R^3, \ldots\) que já conhecemos de GAAL). Mas essencialmente tudo que a gente faz funcionará igualmente bem (ou até melhor) com coeficientes no corpo \(\C\) dos números complexos, e vamos ter utilidade explícita de \(\C\) bem pelo fim do curso. Então segue uma pequena introdução aos números complexos.

O ponto de partida é:

Seja \(i\) o número tal que \(i^2 = -1\).

Observe que \(i\not\in \R\), pois \(a^2\geqslant 0\) para todo \(a\in \R\).

O conjunto \(\C\) dos números complexos é \[\C = \{ a + bi\,|\,a,b\in \R\}.\] Somamos os números complexos assim: \[(a+bi) + (c+di) = (a+c) + (b+d)i,\] e multiplicamos eles assim: \[(a+bi)(c+di) = (ac - bd) + (ad+bc)i.\]

Esta multiplicação faz sentido, lembrando que \(i^2 = -1\), pois: \[(a+bi)(c+di) = ac + adi + bci + bdi^2 = ac + (ad + bc)i + bd(-1) = (ac-bd) + (ad + bc)i.\] Observe que todo número complexo \(a+bi\) diferente de \(0\) possui inverso multiplicativo, nomeadamente \[ \frac{a}{a^2+b^2} - \frac{b}{a^2+b^2}i \] (confirme isso!). Assim \(\C\) é similar ao conjunto \(\R\) de números reais ou ao conjunto \(\Q\) de números racionais. Note que o conjunto \(\Z\) de números inteiros não possui esta propriedade, pois, por exemplo, \(2\in\Z\) não possui inverso em \(\Z\). Isso é porque \(1/2\not\in\Z\). Os conjuntos de onde existem inversos dos seus elementos não nulos chamam-se corpos. Assim \(\Q\), \(\R\) e \(\C\) são corpos, mas \(\Z\) não é corpo. Para fazer álgebra linear, nós precisamos trabalhar com corpos.

Às vezes é útil pensar nos elementos de \(\C\) no plano:

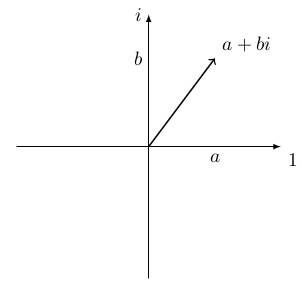
O eixo horizontal chama-se o eixo real (pois os números deste eixo têm a forma \(a+0i = a\in \R\)), enquanto o eixo vertical chama-se o eixo imaginário.

A norma \(\|z\|\) de um número complexo \(z\) é o comprimento do segmento no plano representando \(z\). Logo pelo Teorema de Pitágoras, \[\|a+bi\| = \sqrt{a^2 + b^2}.\]

Definição 38.1 O conjugado complexo de um número complexo \(z = a+bi\) é o número complexo \(\overline{z} = a-bi\).

Logo, o conjugado complexo \(\overline{z}\) de \(z\) é a reflexão de \(z\) no eixo real:

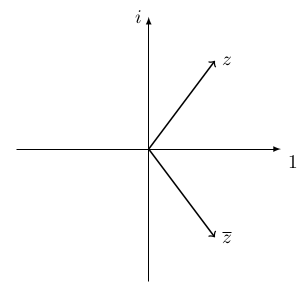
Exercício 38.1 Dados números complexos \(y,z\), mostre que \(\overline{y+z}=\overline y+\overline z\) e que \(\overline{y}\cdot \overline{z} = \overline{yz}\).

Uma fórmula importante pra gente: \[\boxed{z\cdot \overline{z} = \overline{z}\cdot z = \|z\|^2}\] Assumindo que \(z=a+bi\), ela segue por uma conta fácil: \[z\cdot \overline{z} = (a+bi)(a-bi) = a^2 + \cancel{abi} - \cancel{abi} - b^2i^2 = a^2+b^2 = \|z\|^2\quad\checkmark\] Observe também que quando \(z\neq 0\), esta fórmula implica que \[1=\frac{z\cdot \overline z}{\|z\|^2}=\frac{z\cdot \overline z}{a^2+b^2}\] e segue que \(z^{-1}=\overline z/\|z\|=(a-bi)/(a^2+b^2)\) como foi afirmado anteriormente.

Os números complexos têm todas as propriedades legais dos números reais: podemos somar, multiplicar e dividir eles entre si. Mas os números complexos têm uma vantagem enorme sobre os números reais, e por isso são tão importantes na matemática:

Teorema 38.1 [O Teorema Fundamental da Álgebra] Seja \(f(x)\) um polinômio não constante com coeficientes em \(\C\). Existe uma raiz de \(f\) em \(\C\). Isto é, existe \(z\in \C\) tal que \(f(z) = 0\).

A prova deste resultado usa análise complexa e vocês vão estudá-la na disciplina Variável Complexa. Por enquanto, somente vamos olhar um exemplo simples:

Exemplo 38.1 Seja \(f(x) = x^2- 2x + 5\). Pela fórmula quadrática, as raizes de \(f\) são \[\lambda = \frac{2 \pm \sqrt{4 - 20}}{2} = \frac{2 \pm \sqrt{(-1)\cdot 16}}{2} = \frac{2 \pm 4i}{2} = 1\pm 2i.\]

38.3 Espaços Vetoriais

Exemplo 38.2 Os espaços vetoriais que conhecemos de GAAL são:

\(\R^1 = \R\)
\(\R^2 = \{(x,y)\,|\,x,y\in \R\}\quad\) (o “plano”)
\(\R^3 = \{(x,y,z)\,|\,x,y,z\in \R\}\quad\)(o “espaço”)
\(\R^n = \{(x_1,\ldots,x_n)\,|\,x_1,\ldots,x_n\in \R\}\quad\)(“espaço \(n\)-dimensional”).

Com os elementos destes conjuntos, a gente pode fazer duas coisas principais:

Somar dois elementos. Por exemplo, em \(\R^2\) a gente tem: \[(w,x) + (y,z) = (w + y, x + z).\]
Multiplicar um elemento por um escalar \(\lambda\in \R\). Por exemplo, em \(\R^2\) a gente tem \[\lambda\cdot (x,y) = (\lambda x, \lambda y).\]

Tais operações têm várias propriedades que ajudam com as contas. Por exemplo dados \(\ul{u}, \ul{v}\in \R^2\) e \(\lambda \in \R\), temos \[\lambda(\ul{u} + \ul{v}) = \lambda\ul{u} + \lambda\ul{v}.\]

Vamos definir agora um espaço vetorial em geral, usando propriedades assim para definí-lo:

Definição 38.2 Um espaço vetorial sobre \(\R\) é um conjunto \(V\) de elementos (chamados “vetores”) junto com as operações da soma (\(\ul{u}, \ul{v}\in V \implies \ul{u}+\ul{v}\in V\)) e do produto por escalar (\(\ul{u}\in V, \lambda\in \R \implies \lambda\ul{u}\in V\)). As operações têm que satisfazer as seguintes condições

\((\ul{u}+\ul{v})+\ul{w} = \ul{u} + (\ul{v} + \ul{w})\quad \forall \ul{u}, \ul{v}, \ul{w}\in V\) (“associatividade"),
\(\ul{u} + \ul{v} = \ul{v} + \ul{u}\quad \forall\ul{u}, \ul{v}\in V\) (“commutatividade”),
Existe um elemento \(\ul{0}\in V\) tal que \[\ul{u} + \ul{0} = \ul{u}\quad\forall \ul{u}\in V.\]
Para cada \(\ul{u}\in V\), existe um elemento \(-\ul{u}\in V\) tal que \[\ul{u} + (-\ul{u}) = \ul{0},\]
\(\lambda(\ul{u} + \ul{v}) = \lambda\ul{u} + \lambda\ul{v}\quad\forall \lambda\in \R, \forall \ul{u}, \ul{v}\in V\),
\((\lambda + \mu)\ul{u} = \lambda\ul{u} + \mu\ul{u}\quad\forall \lambda, \mu\in \R, \forall\ul{u}\in V\),
\((\lambda\mu)\ul{u} = \lambda(\mu \ul{u})\quad\forall \lambda, \mu\in \R, \forall\ul{u}\in V\),
\(1\cdot \ul{u} = \ul{u}\quad \forall \ul{u}\in V\).

O conceito do “espaço vetorial sobre \(\C\)” pode ser definido na mesma maneira trocando as ocorrências de “\(\R\)” com “\(\C\)” na definição acima. Na primeira lista dos exercícios, haverá um exercício que pede que você enuncie a definição sobre \(\C\). Nesta disciplina nós vamos trabalhar principalmente com espaços vetoriais sobre \(\R\), mas você deve saber que o mesmo estudo pode ser feito com espaços vetoriais sobre \(\C\). Espaços vetoriais sobre \(\C\) vão aparecer mais na disciplina Álgebra Linear II.

Dados \(\ul{u}, \ul{v}\in V\), vamos denotar por \(\ul{u} - \ul{v}\) o elemento \(\ul{u} + (-\ul{v})\). A partir dessas propriedades, podemos deduzir outras. Por exemplo:

Lema 38.1 \(0\cdot\ul{u} = \ul{0}\,\,\,\forall\ul{u}\in V\).

Comprovação. Temos \[0\ul{u} + \ul{u} \overset{P8}{=} 0\ul{u} + 1\ul{u} \overset{6}{=} (0+1)\ul{u} = 1\ul{u} \overset{8}{=} \ul{u}.\qquad (*)\] Logo: \[0\ul{u} \overset{3}{=} 0 \ul{u} + \ul{0} \overset{4}{=} 0\ul{u} + \ul{u} -\ul{u} \overset{(*)}{=} \ul{u} -\ul{u} \overset{4}{=} \ul{0}.\]

Exemplo 38.3

\(\R^n\) é um espaço vetorial \(\forall n\). Exercício: confirme que \(\R^n\) satisfaz as propriedades 1–8.
Quando \(n=1\) acima, obtemos que \(\R = \R^1\) é um espaço vetorial sobre \(\R\). As operações da soma e da multiplicação por escalar são simplemente a soma e o produto de números reais: \[(a) + (b) = (a+b)\] \[\lambda(a) = (\lambda a).\]
O menor espaço vetorial de todos: \(\{\ul{0}\}\) é um espaço vetorial. Temos somente um jeito de definir a soma e produto por escalar: \[\ul{0} + \ul{0} = \ul{0}\] \[\lambda\cdot \ul{0} = \ul{0}.\] Este espaço parece meio idiota, mas ele é muito importante.
Denote por \(M_{m,n}(\R)\) o conjunto das matrizes \(m\times n\) com entradas em \(\R\). Se lembre que podemos somar duas matrizes em \(M_{m,n}(\R)\): \[\hbox{Se }A = (a_{ij}), B = (b_{ij})\in M_{m,n}(\R)\hbox{ então } A+B = (a_{ij} + b_{ij}) \in M_{m,n}(\R).\] Também podemos multiplicar uma matriz por um escalar: \[\hbox{Se }A = (a_{ij})\in M_{m,n}(\R)\,,\,\lambda\in \R\hbox{ então } \lambda A = (\lambda a_{ij}) \in M_{m,n}(\R).\] De fato, com essas operações, \(M_{m,n}(\R)\) é um espaço vetorial. Confirmo, por exemplo, que satisfaz Propriedade 3. A matriz \(\ul{0}\) será a matriz cujas entradas são todas \(0\): \[\ul{0} = \begin{pmatrix} 0 & \cdots & 0 \\ \vdots & \ddots & \vdots\\ 0 & \cdots & 0 \end{pmatrix}.\] Para qualquer matriz \(A = (a_{ij})\) a gente tem \[A + \ul{0} = (a_{ij}) + (0) = (a_{ij} + 0) = (a_{ij}) = A.\quad\checkmark\] Exercício: confirme que mais algumas das propriedades valem.

Os espaços \(M_{1,n}(\R)\) e \(M_{n,1}(\R)\) são os espaços de vetores linhas e de vetores colunas, respetivamente, de comprimento \(n\) sobre \(\R\). Estes espaços serão identificados com \(\R^n\).
Um exemplo menos óbvio. Seja \(X\) um conjunto qualquer e considere o conjunto das funções (= aplicações) de \(X\) a \(\R\): \[\mathcal{F}(X, \R) = \{ f : X\to \R\hbox{ uma função}\}.\] Podemos definir a soma de duas funções: Dadas funções \(f,g : X\to \R\), definimos uma função nova \((f+g) : X\to \R\) como \[(f+g)(x) := f(x) + g(x).\] Também podemos definir o produto por escalar de uma função \(f\) pelo escalar \(\lambda\) assim: \[(\lambda f)(x) := \lambda\cdot f(x).\] Com essas operações, \(\mathcal{F}(X, \R)\) é um espaço vetorial. Vamos confirmar umas propriedades:
- Dadas funções \(f,g:X\to \R\), queremos confirmar que as funções \(f+g\) e \(g+f\) são iguais. Para fazer isso, temos que confirmar que \((f+g)(x) = (g+f)(x)\) para todo \(x\in X\). Mas isso é fácil: \[(f+g)(x) = f(x) + g(x) = g(x) + f(x) = (g+f)(x).\]
- A função \(\ul{0}\in \mathcal{F}(X,\R)\) será a função que leva todo \(x\in X\) pro elemento \(0\in \R\). Ou seja, \(\ul{0}(x) := 0\,\forall x\in X\). Temos que confirmar que \(f+\ul{0} = f\), logo temos que confirmar que \((f+\ul{0})(x) = f(x)\,\forall x\in X\). Mas \[(f+\ul{0})(x) = f(x) + \ul{0}(x) = f(x) + 0 = f(x).\]
Exercício: Defina a função “\(-f\)” e confirme que as outras propriedades valem.

38.4 Subespaços

Um subespaço \(W\) de um espaço vetorial \(V\) será um espaço vetorial “menor” contido dentro de \(V\). Observe que um espaço vetorial possui vários subespaços diferentes:

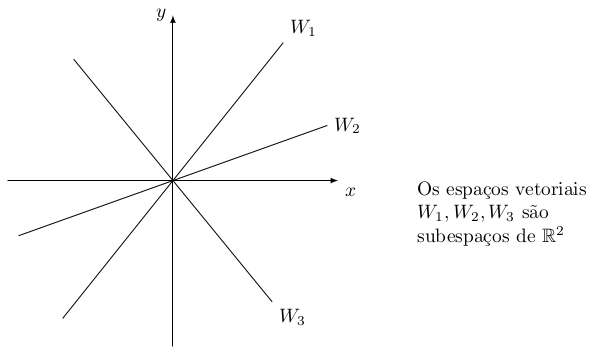
Vamos passar tempo estudando como os subespaços de um espaço vetorial podem interagir entre si. Definição formal:

Definição 38.3 Um subespaço do espaço vetorial \(V\) é um subconjunto não vazio \(W\) de \(V\) tal que

\(\ul{u}, \ul{v}\in W \implies \ul{u} +\ul{v} \in W\),
\(\ul{u}\in W\) e \(\lambda\in \R \implies \lambda\ul{u}\in W\).

Quando \(W\) é um subespaço de \(V\), vamos às vezes escrever \(W\leqslant V\).

Outras propriedades seguem da definição:

FATO: Para todo subespaço \(W\) de \(V\), \(\ul{0}\in W\).

\(W\neq \varnothing\), então existe algum \(\ul{w}\in W\). Mas agora \[0\cdot \ul{w} = \ul{0} \in W\] pela segunda condição de subespaço.

Confirme que um subespaço \(W\) de \(V\) é de fato um espaço vetorial. A definição de subespaço é mais curta pois certas propriedades seguem automaticamente. Por exemplo, \(\forall \ul{u}, \ul{v}, \ul{w}\in W\) temos que \[(\ul{u} + \ul{v}) + \ul{w} = \ul{u} + (\ul{v} + \ul{w})\] pois essa propriedade já vale em \(V\).

Exemplo 38.4 Seja \(V\) um espaço vetorial. Uns subespaços de \(V\):

\(\{\ul{0}\}\leqslant V\), pois \(\ul{0}+\ul{0} = \ul{0}\in \{\ul{0}\}\) e \(\lambda\ul{0} = \ul{0}\in \{\ul{0}\}\) para qualquer \(\lambda\in \R\).
\(V\leqslant V\).
Seja \(\ul{w}\) um vetor qualquer de \(V\) e seja \(W = \{\lambda\ul{w}\,|\,\lambda\in \R\}\) o conjunto de todos os múltiplos escalares de \(\ul{w}\). Então \(W\leqslant V\): \[\lambda\ul{w}, \mu\ul{w}\in W \implies \lambda\ul{w} + \mu\ul{w} = (\lambda + \mu)\ul{w} \in W\quad\checkmark\] \[\lambda\ul{w}\in W, \mu\in \R \implies \mu(\lambda\ul{w}) = (\mu\lambda)\ul{w}\in W.\quad\checkmark\] Subespaços dessa forma em \(\R^n\) são retas que passam pela origem, como os subespaços \(W_1,W_2,W_3\) no diagrama acima.

38.5 Subespaços e sistemas lineares

Se lembre que um sistema linear é uma equação da forma \[AX = B\] em que \(A,X,B\) são as matrizes \[A = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ \vdots & \ddots & & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix}\,,\, X = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}\,,\, B = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{pmatrix}.\] As entradas de \(A,B\) são números, enquanto as entradas de \(X\) são variáveis. Uma solução do sistema acima é uma matriz \(n\times 1\), \(S\) (de números) tal que a equação \[AS = B\] vale.

Exemplo 38.5 Por exemplo, o sistema linear \[\begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 3 \\ 0 \end{pmatrix}\] tem solução \(S = \begin{pmatrix} 1 \\ 2 \end{pmatrix}\), pois \[\begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix} \begin{pmatrix} 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 1+2 \\ 0+0 \end{pmatrix} = \begin{pmatrix} 3 \\ 0 \end{pmatrix}.\qquad\checkmark\] O conjunto das soluções deste sistema é \[\mathcal{S} = \left\{\left. \begin{pmatrix} 3-\alpha \\ \alpha \end{pmatrix} \,\right|\, \alpha\in \R\right\}.\] Observe que \(\mathcal{S}\) não é um subespaço de \(\R^2\): por exemplo, \[\begin{pmatrix} 1 \\ 2 \end{pmatrix}\,,\, \begin{pmatrix} 2 \\ 1 \end{pmatrix} \in \mathcal{S}\quad\hbox{mas}\quad \begin{pmatrix} 1 \\ 2 \end{pmatrix}+\begin{pmatrix} 2 \\ 1 \end{pmatrix} = \begin{pmatrix} 3 \\ 3 \end{pmatrix}\not\in \mathcal{S}.\]

MAS: Um sistema homogêneo é um sistema linear da forma \[AX = \ul{0}.\] Temos

Lema 38.2 O conjunto solução de um sistema homogêneo \(AX = \ul{0}\) com \(n\) variáveis é um subespaço de \(\R^n\).

Comprovação. Observe primeiro que o conjunto solução não é vazio, pois \(\ul{0}\) é sempre uma solução de um sistema homogêneo. Vamos confirmar as outras propriedades de subespaço. Sejam \(S,T\) soluções do sistema. Então \[A(S+T) = AS + AT = \ul{0} + \ul{0} = \ul{0},\] logo \(S+T\) também é solução. Sejam \(\lambda\in \R\) e \(S\) uma solução. Então \[A(\lambda S) = \lambda AS = \lambda\ul{0} = \ul{0},\] logo \(\lambda S\) também é uma solução. Então o conjunto solução do sistema homogêneo \(AX=B\) é um subespaço de \(\R^n\).