8 Funções

8.1 Definições básicas relacionadas com funções

Definição 8.1 Sejam $A$ e $B$ conjuntos. Uma função de $A$ em $B$ é uma relação $R\subseteq A\times B$ tal que

$\forall a\in A:(\exists b\in B: aRb)$;
Se $aRb_1$ e $aRb_2$ com algum $a\in A$ e $b_1,b_2\in B$, então $b_1=b_2$.

Em outras palavras, \[ \forall a\in A:(\exists b\in B\mbox{ único }:aRb). \] O quantificador “existe único” é frequentamente denotado pelo símbolo “$\exists!$”. Usando esta notação, pode-se escrever que \[ \forall a\in A:(\exists! b\in B:aRb). \] Quando $R\subseteq A\times B$ é uma função e $aRb$, então escrevermos que $b=R(a)$ ou às vezes que $R:a\mapsto b$. Nós frequentemente usamos as palavras, mapa, mapeamento, aplicação, correspondência em vez de função.

Exemplo 8.1 Seja $A=\{1,2,3\}$ e $B=\{1,3,5,7\}$. As seguintes relações são funções: \[\begin{align*} R_1&=\{(1,3),(2,3),(3,5)\};\\ R_2&=\{(1,3),(2,3),(3,3)\};\\ R_2&=\{(1,3),(2,7),(3,5)\}. \end{align*}\] As seguintes não são funções: \[\begin{align*} R_4&=\{(1,3),(2,3)\};\\ R_5&=\{(1,3),(2,3),(3,3),(2,7)\};\\ \end{align*}\]

Definição 8.2 Se $R\subseteq A\times B$ é uma função, então escrevemos $R$ na forma \[ R:A\to B,\quad a\mapsto R(a). \] O conjunto $A$ é chamado de domínio, o conjunto $B$ é o codomínio ou contradomínio da função $R$. A imagem de $R$ está definida como \[ \mbox{Im}(R)=R(A)=\{R(a)\mid a\in A\}. \]

Quando definimos uma função, precisa-se explictar três coisas:

o domínio da função;
o contradomínio da função;
a correspondência entre os elementos do domínio e os elementos do contradomínio.

Duas funções $f$ e $g$ serão consideradas iguais, se os seus domínios são iguais, seus codomínios são iguais, e as correspondências entre o domínio e o codomínio são as mesmas; ou seja $f(x)=g(x)$ vale para todo elemento $x$ no domínio.

Por exemplo, falar da “função seno” é ambíguo, pois não se sabe assim o seu domínio e o contradomínio. Por outro lado, as seguntes funções são bem definidas: \[ \sen:\R\to \R,\ x\mapsto \sen x \tag{8.1}\] ou \[ \sen:\R\to [-1,1],\ x\mapsto \sen x. \tag{8.2}\] As funções dadas pelas equações Equação 8.1 e Equação 8.2 serão consideradas distintas; veja também o Exemplo 8.3 abaixo.

Exemplo 8.2 No caso da função $R_1$ do Exemplo 8.1, escrevemos que \[ R_1:A\to B,\ R(1)=3,\ R(2)=3,\ R(3)=5 \] ou que \[ R_1:A\to B,\ 1\mapsto 3,\ 2\mapsto 3,\ 3\mapsto 5. \] Observe o uso das flechas “$\to$” e “$\mapsto$”. O domínio de $R_1$ é o conjunto $A=\{1,2,3\}$, o contradomínio é $A=\{1,3,5,7\}$, a imagem de $R_1$ é $\{3,5\}$. Note que a imagem é estritamente menor que o contradomínio.

Definição 8.3 Seja $f:A\to B$ uma função.

A função $f$ é sobrejetiva (ou sobrejetora) se $\mbox{Im}(f)=B$. Formalmente, \[ \forall b\in B:(\exists a\in A:b=f(a)). \]
A função $f$ é injetiva (ou injetora) quando $f(a_1)=f(a_2)$ implica que $a_1=a_2$ para todo $a_1,a_2\in A$.
A função $f$ é bijetiva (bijetora) se ela é sobrejetiva e injetiva.

Exemplo 8.3 Seja $\R_+=\{x\in\R\mid x\geq 0\}$. Considere as funções \[ g:\R\to \R,\ g(x)=x^2,\quad f:\R\to \R_+,\ f(x)=x^2. \] As funções $f$ e $g$ parecem iguais, mas elas são consideradas diferentes, pois os codimonínios são diferentes. De fato, $f$ é sobrejetiva, mas $g$ não é. Se considere a função \[ h:\R_+\to\R_+,\ h(x)=x^2, \] então $h$ é injetiva e sobrejetiva, então ela é bijetiva.

Exemplo 8.3 explica porque é importante explicitar o domínio e o contradomínio na definição de uma função. Observe também que a função $\sen$ definida em Equação 8.1 não é sobrejetiva, enquando a função $\sen$ definida em Equação 8.2 é sobrejetiva. Portanto, não faz sentido perguntar se “a função seno é sobrejetiva?” ou se a “função $x^2$ é injetiva?”. Precisa esclarecer o domínio e o codomínio para respoder estes tipos de perguntas.

Exemplo 8.4 Se $A$ é um conjunto qualquer, então a função identidade em $A$ é a função \[ \mbox{id}_A:A\to A,\ \mbox{id}_A(a)=a. \] A função $\mbox{id}_A$ é bijetiva.

Exemplo 8.5 Por exemplo, se $A=\{-1,0,1\}$, então \[ \mbox{id}_A:A\to A,\ -1\mapsto -1,\ 0\mapsto 0,\ 1\mapsto 1. \]

8.2 A composição de funções

Definição 8.4 Sejam $f:A\to B$ e $g:B\to C$ funções. Definimos $g\circ f:A\to C$ como a função \[ g\circ f:A\to C,\quad (g\circ f)(a)=g(f(a))\quad\mbox{para todo }a\in A. \]

Exercício 8.1 Verifique que $g\circ f:A\to C$ é de fato uma função.

Exemplo 8.6 Assuma que $A=\{1,2,3\}$, $B=\{3,4\}$, e $C=\{2,4,6,8\}$. Sejam \[ f:A\to B,\quad 1\mapsto 3,\ 2\mapsto 3,\ 3\mapsto 4 \] e \[ g:B\to C,\quad 3\mapsto 6,\ 4\mapsto 2. \] Então \[ g\circ f:\{1,2,3\}\to \{2,4,6,8\},\quad 1\mapsto 6,\ 2\mapsto 6,\ 3\mapsto 2. \]

Exemplo 8.7 Sejam \[ f:\R\to [-1,1],\ f(x)=\sen x\quad\mbox{e}\quad h:[-1,1]\to [0,1],\ h(x)=x^2. \] Então a composição destas duas funções é a função \[ g\circ f:\R\to [0,1],\ (g\circ f)(x)=\sen^2(x). \]

Lema 8.1 Sejam $f:A\to B$, $g:B\to C$, $h:C\to D$ funções. Então

$h\circ (g\circ f)=(h\circ g)\circ f$;
$f\circ \mbox{id}_A=f$;
$\mbox{id}_B\circ f=f$.

Comprovação.

Note que o domínio de $h\circ (g\circ f)$ e de $(h\circ g)\circ f$ é o conjunto $A$ e o codomínio de ambas é $C$. Então precisa provar que $(h\circ (g\circ f))(a)=((h\circ g)\circ f)(a)$ para todo $a\in A$. Isso segue, pois \[ (h\circ (g\circ f))(a)=h((g\circ f)(a))=h(g(f(a))) \] e \[ ((h\circ g)\circ f)(a)=(h\circ g)(f(a))=h(g(f(a))). \]
Note que $f\circ \mbox{id}_A:A\to B$. Precisa provar então que $(f\circ \mbox{id}_A)(a)=f(a)$ para todo $a\in A$. Isso segue, pois \[ (f\circ \mbox{id}_A)(a)=f(\mbox{id}_A(a))=f(a). \]
Use o argumento na demonstração de 2.

Lema 8.2 Sejam $f:A\to B$ e $g:B\to C$ funções.

Se $g\circ f:A\to C$ é sobrejetiva, então $g$ é sobrejetiva.
Se $g\circ f:A\to C$ é injetiva, então $f$ é injetiva.

Comprovação.

Assuma que $g\circ f:A\to C$ é sobrejetiva. Seja $c\in C$. Precisa provar que existe $b\in B$ tal que $g(b)=c$. Sabendo que $g\circ f$ é sobrejetiva, existe $a\in A$ tal que \[ c=(g\circ f)(a)=g(f(a)). \] Logo, tomando $b=f(a)$, temos que $g(b)=g(f(a))=c$. Ou seja, $g$ é sobrejetiva.
Assuma que $a_1,a_2\in A$ tal que $f(a_1)=f(a_2)$. Precisamos provar que $a_1=a_2$. Primeiro, observe que \[ (g\circ f)(a_1)=g(f(a_1))=g(f(a_2))=(g\circ f)(a_2). \] Sabendo que $g\circ f$ é injetiva, isso implica que $a_1=a_2$ e que $f$ é injetiva.

8.3 Funções inversas

Definição 8.5 Seja $f:A\to B$ uma função.

Uma função $g:B\to A$ é dita inversa de $f$ à esquerda se $g\circ f=\mbox{id}_A$.
Uma função $g:B\to A$ é dita inversa de $f$ à direita se $f\circ g=\mbox{id}_B$.
Uma função $g:B\to A$ é dita inversa de $f$ se $g\circ f=\mbox{id}_A$ e $f\circ g=\mbox{id}_B$. Neste caso, dizemos que $f$ é invertível.

Exemplo 8.8 Seja $A=\{1,2,3\}$ e $B=\{4,5\}$. Considere as funções \[ f:A\to B,\ 1\mapsto 4,\ 2\mapsto 4,\ 3\mapsto 5 \] e \[ g:B\to A,\ 4\mapsto 1,\ 5\mapsto 3. \] Calculando que \[ (f\circ g)(4)=f(g(4))=f(1)=4\quad \mbox{e}\quad (f\circ g)(5)=f(g(5))=f(3)=5 \] obtemos que \[ f\circ g=\mbox{id}_B. \] Ou seja $g$ é inversa à direita de $f$ e $f$ é inversa à esquerda de $g$. Note que $g$ não é a única inversa à direita de $f$; de fato, definindo \[ g_1:B\to A,\ 4\mapsto 2,\ 5\mapsto 3. \] é também inversa à direita de $f$. Similarmente, \[ f_1:A\to B,\ 1\mapsto 4, 2\mapsto 5,\ 3\mapsto 5 \] é também inversa à esquerda de $g$. O leitor pode verificar que nem $f$, nem $g$ possuem inversas.

Note que no Exemplo 8.8, as inversas existem pois $f$ é sobrejetiva e $g$ é injetiva. Por outro lado, estas funções não são bijetivas, e não têm inversas.

Lema 8.3 Seja $f:A\to B$ uma função. Então

$f$ tem inversa à direita se e somente se $f$ é sobrejetiva.
$f$ tem inversa à esquerda se e somente se $f$ é injetiva.
$f$ tem inversa se e somente se $f$ é bijetiva. Ou seja, uma função $f$ é invertível se e somente se ela é bijetiva.

Comprovação.

Assuma que $f$ possui inversa $g$ à direita. Então $f\circ g=\mbox{id}_B$. Como $\mbox{id}_B$ é sobrejetiva, temos, por Lema 8.2 que $f$ é sobrejetiva. Vice versa, assuma que $f:A\to B$ é sobrejetiva. Defina $g:B\to A$ na seguinte maneira. Se $b\in B$, então existe $a_b\in A$ tal que $f(a_b)=b$ (pois, $f$ é sobrejetiva). Escolha um tal $a_b$ para todo $b$ (pode existir vários) e defina $g(b)=a_b$. Então temos, para $b\in B$, que \[ (f\circ g)(b)=f(g(b))=f(a_b)=b. \] Ou seja, $f\circ g=\mbox{id}_B$ e $g$ é inversa à direita de $f$.
Assuma que $f$ tem inversa $g$ à esquerda. Então $g\circ f=\mbox{id}_A$. Como $\mbox{id}_A$ é injetiva, temos que $f$ é injetiva por Lema 8.2. Vice versa, assuma que $f$ é injetiva. Defina a função $g:B\to A$ na seguinte forma. Se $a\in A$, então existe único $b\in B$ tal que $f(a)=b$. Além disso, para este $b\in B$, $a\in A$ é o único elemento tal que $f(a)=b$ (pois $f$ é injetiva). Portanto, pode-se definir $g(b)=a$ para $b\in\mbox{Im}(f)$. Se $b\not\in\mbox{Im}(f)$, escolhe algum elemento arbitrário $a\in A$ e defina $g(b)=a$. Neste caso, \[ (g\circ f)(a)=g(f(a))=g(b)=a. \] Ou seja, $g\circ f=\mbox{id}_A$ e $g$ é inversa à esquerda de $f$.
Se $f$ tem inversa $g$, então $g$ é inversa de $f$ à direita e à esquerda. Portanto, pelos itens 1.-2., $f$ é sobrejetiva e também injetiva. Portanto, $f$ é bijetiva.

Definição 8.6 Se $f:A\to B$ é uma função e $g:B\to A$ é inversa de $f$, então escrevemos que $g=f^{-1}$.

8.4 Um exemplo de GAAL

Exemplo 8.9 Considere o espaço $\R^2$ de vetores colunas $\begin{pmatrix} x\\ y\end{pmatrix}$ e seja $A$ uma matriz $(2\times 2)$. Defina a função \[ f_A:\R^2\to \R^2,\quad f_A\begin{pmatrix} x\\ y\end{pmatrix}=A\begin{pmatrix} x\\ y\end{pmatrix} \] (multiplicação matricial).

Assuma que $A$ é uma matriz invertível e seja $B$ sua inversa. Temos que $AB=BA=I_2$ onde $I_2$ é a matriz identidade $(2\times 2)$. Neste caso \[ f_B\circ f_A:\R^2\to \R^2,\quad (f_B\circ f_A) \begin{pmatrix} x\\ y\end{pmatrix}=f_B\left(f_A\begin{pmatrix} x\\ y\end{pmatrix}\right)=BA\begin{pmatrix} x\\ y\end{pmatrix}=I_2\begin{pmatrix} x\\ y\end{pmatrix}=\begin{pmatrix} x\\ y\end{pmatrix}. \] Similarmente, \[ f_A\circ f_B:\R^2\to \R^2,\quad (f_A\circ f_B) \begin{pmatrix} x\\ y\end{pmatrix}=f_A\left(f_B\begin{pmatrix} x\\ y\end{pmatrix}\right)=AB\begin{pmatrix} x\\ y\end{pmatrix}=I_2\begin{pmatrix} x\\ y\end{pmatrix}=\begin{pmatrix} x\\ y\end{pmatrix}. \] Portanto $f_B\circ f_A=f_A\circ f_B=\mbox{id}_{\R^2}$. Ou seja, $f_A$ é invertível e sua inversa é $f_B=f_{A^{-1}}$.

Assuma agora que $A$ é uma matriz não invertível (singular) e considere a função $f_A:\R^2\to \R^2$. Assuma que \[ A=\begin{pmatrix} a & b \\ c & d\end{pmatrix}. \] Sabemos de GAAL que o sistema \[\begin{eqnarray*} ax+by&=0\\ cx+dy&=0 \end{eqnarray*}\] tem infinitas soluções. Se $\begin{pmatrix} x\\ y\end{pmatrix}$ é uma solução deste sistema, então \[ f_A\begin{pmatrix} x\\ y\end{pmatrix}=\begin{pmatrix} 0\\ 0\end{pmatrix}. \] Em particular, $f_A$ não é injetiva. Similarmente, aprendemos também em GAAL que existe $\begin{pmatrix} b_1\\ b_2\end{pmatrix}\in\R^2$ tal que o sistema \[\begin{eqnarray*} ax+by&=b_1\\ cx+dy&=b_2 \end{eqnarray*}\] não possui solução. Neste caso $\begin{pmatrix} b_1\\ b_2\end{pmatrix}\in\R^2\setminus\mbox{Im}(f_A)$ e $f_A$ não é sobrejetiva. Ou seja, assumindo que $A$ é uma matriz não invertível, $f_A$ não tem nem inversa à direita nem inversa à esquerda.

8.5 Restrição de $f$

Definição 8.7 Seja $f:A\to B$ uma função e $C\subseteq A$. Definimos a restrição de $f$ para $C$ como a função \[ f|_C:C\to B,\quad c\mapsto f(c)\quad\mbox{para todo }c\in C. \]

Exemplo 8.10 Considere a função $\sen:\R\to [-1,1]$. A função $\sen$ é sobrejetiva, mas não é injetiva, pois $\sen(0)=\sen(\pi)=0$.

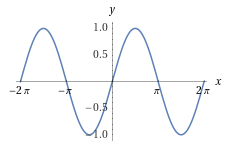
Por outro lado, pode-se considerar a restrição \[ \sen|_{[-\pi/2,\pi/2]}:[-\pi/2,\pi/2]\to [-1,1]. \]

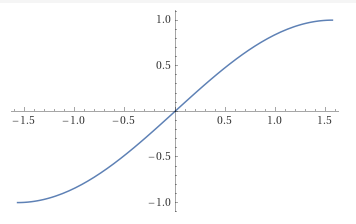
A função $\sen|_{[-\pi/2,\pi/2]}:[-\pi/2,\pi/2]\to[-1,1]$ é injetiva e sobrejetiva, em particular, ela é invertível. A sua inversa é a função \[ \mbox{arcssen}:[-1,1]\to [-\pi/2,\pi/2]. \]

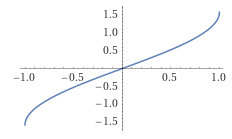
8.6 Imagens e pré-imagens

Definição 8.8 Seja $f:A\to B$ uma função.

Se $X\subseteq A$, então a imagem de $X$ por $f$ está definida por \[ f(X)=\{f(x)\mid x\in X\} \]
Se $Y\subseteq B$, então a pré-imagem de $Y$ por $f$ está definida por \[ f^{-1}(Y)=\{a\in A\mid f(a)\in Y\}. \] Note que $f(X)\subseteq B$ e $f^{-1}(Y)\subseteq A$. Note também a escrever $f^{-1}$ não indica que $f$ é invertível! A pré-imagem está definida para funções que não necessariamente são invertíveis.

Exemplo 8.11 Seja $A=\{1,2,3,4\}$, $B=\{2,4,6,8\}$ e \[ f:A\to B,\quad 1\mapsto 2,\ 2\mapsto 2,\ 3\mapsto 6,\ 4\mapsto 8. \] Então temos as seguintes imagens e pré-imagens:

$f(\{1,2\})=\{2\}$;
$f(\{3\})=\{6\}$;
$f(\{1,2,3\})=\{2,6\}$;
$f(\emptyset)=\emptyset$
$f(A)=\mbox{Im}(f)=\{2,6,8\}$;
$f^{-1}(\{2\})=\{1,2\}$;
$f^{-1}(\{4\})=\emptyset$;
$f^{-1}(\{2,6\})=\{1,2,3\}$.

Note que $f^{-1}(\{y\})$ pode ser também escrito como $f^{-1}(y)$. Por exemplo, $f^{-1}(2)=\{1,2\}$. Mas é importante observar que $f^{-1}(2)$ neste contexto não é um elemento, mas um subconjunto do domínio. Nós nesta disciplina vamos escrever $f^{-1}(\{y\})$ para evitar confusão.

Exemplo 8.12 Considere a função $\sen:\R\to[-1,1]$. Temos as seguintes imagens e pré-imagens:

$f([0,\pi])=f([0,\pi/2])=[0,1]$;
$f([-\pi/2,\pi/2])=[-1,1]$;
$f^{-1}(\{0\})=\{k\pi\mid k\in\Z\}$;
$f^{-1}(\{1\})=\{\pi/2+2k\pi\mid k\in\Z\}$;
\[ f^{-1}([0,1])=\cdots \cup[-2\pi,-\pi]\cup[0,\pi]\cup[2\pi,3\pi]\cup\cdots =\bigcup_{k\in\Z}[2k\pi,(2k+1)\pi]. \]

8.7 Pré-imagens na natureza

Vamos considerar dois exemplos de pré-imagens que aparecem nas disciplinas GAAL e Cálculo I.

Exemplo 8.13 Considere a função $f:\R^2\to \R$ definida por $f(x,y)=x+y$. É fácil verificar que $f$ é sobrejetiva, mas não é injetiva. Vamos determinar $f^{-1}(\{0\})$. Note que \[ f(x,y)=0\quad\mbox{se e somente se}\quad x+y=0. \] Então $f^{-1}(\{0\})$ é composta dos pontos $(x,y)\in\R^2$ no plano tal que $x+y=0$. Note que estes pontos formam uma reta no plano $\R^2$ ilustrada como a reta azul no seguinte desenho.

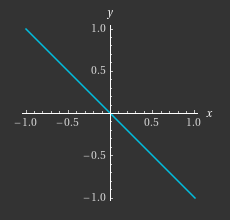
O que é a pré-imagem $f^{-1}(\{a\})$ com algum $a\in\R$ arbitrário? Neste caso temos que $(x,y)\in f^{-1}(\{a\})$ se e somente se $x+y=a$. Estes pontos também formam uma reta paralela com a reta azul no desenho anterior que passa pelo ponto $(0,a)$. Por exemplo, $f^{-1}(\{-1\})$ é ilustrado no seguintes desenho.

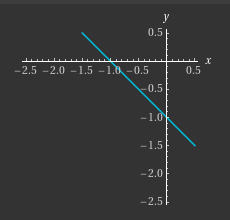
Obtevemos que a pré-imagem $f^{-1}(a)$ é a reta com a equação geral $x+y=a$ e as pré-imagens são as retas paralelas com a reta cuja equação geral é $x+y=0$

Exemplo 8.14 Seja $P$ o conjunto das funções polinomiais $\R\to\R$; mais precisamente, \[ P=\{f:\R\to\R\mid f(x)=a_nx^n+\cdots+a_1x+a_0\mbox{ com $n\geq 0$ e $a_i\in\R$}\}. \] Defina a função \[ d:P\to P,\quad d(f)=f' \] onde $f'$ é o derivado de $f$. Denotemos por $0$ a função constante nula e vamos determinar $d^{-1}(\{0\})$. Temos que $f\in d^{-1}(\{0\})$ se e somente se $f'=0$. Mas sabemos de cálculo que $f'=0$ vale se e somente se $f$ é uma função constante. Obtemos então \[ d^{-1}(\{0\})=\{f\in P\mid \mbox{$f$ é constante}\}. \] Vamos determinar $f^{-1}(\{x+1\})$. Temos que $f\in f^{-1}(\{x+1\})$ se e somente se $f'=x+1$. Temos pelas regras do derivado que isso vale se e somente se $f=(1/2)x^2+x+c$ com algum $c\in\R$ constante. Obtemos então que \[ d^{-1}(\{x+1\})=\left\{\frac 12x^2+x+c\mid c\in\R\right\}. \] Note que os elementos de $d^{-1}(f)$ são chamados de primitivos da função $f$.

8.1 Definições básicas relacionadas com funções

8.2 A composição de funções

8.3 Funções inversas

8.4 Um exemplo de GAAL

8.5 Restrição de \(f\)

8.6 Imagens e pré-imagens

8.7 Pré-imagens na natureza