62 O produto tensorial

62.1 Mapas bilineares

Nesta página $U$ e $V$ são $\F$-espaços vetoriais com algum corpo $\F$.

Definição 62.1 Uma aplicação $f: U \times V \to W$ é chamada de bilinear se, para todos $u, u_1, u_2 \in U$, $v, v_1, v_2 \in V$ e $\alpha, \beta \in \F$, as seguintes propriedades forem satisfeitas:

$f(u_1 + u_2, v) = f(u_1, v) + f(u_2, v)$;
$f(u, v_1 + v_2) = f(u, v_1) + f(u, v_2)$;
$f(\alpha u, v) = \alpha f(u, v)$;
$f(u, \beta v) = \beta f(u, v)$.

O conjunto de todas as aplicaçẽs bilineares $U\times V\to W$ é denotado por \[ \mbox{Bil}(U\times V,W). \]

Exercício 62.1 Mostre que $\mbox{Bil}(U\times V,W)$ é um $\F$-espaço vetorial definindo as operações entre aplicações bilineares.

Exemplo 62.1 Um exemplo clássico de forma bilinear é o produto interno em espaços vetoriais reais. Por exemplo, se $V = \R^n$, o produto interno padrão em $\R^n$ é a aplicação $\R^n \times \R^n \to \R$ definida por: \[ (u,v)\mapsto u \cdot v = \sum_{i=1}^n u_i v_i, \] onde $u = (u_1, u_2, \ldots, u_n)$ e $v = (v_1, v_2, \ldots, v_n)$ são vetores em $\R^n$.

Exercício 62.2 Vimos no Lema 59.1 que quando $B$ é base de $V$ e $W$ é um espaço qualquer, então toda aplicação $B\to W$ pode ser estendida a uma única transformação linear. Uma coisa similar vale com aplicações bilineares. Sejam $B$ e $C$ bases de $U$ e $V$ respetivamente, e seja $f:B\times C\to W$ uma aplicação qualquer.

Demonstre que existe uma única aplicação bilinear $\tilde f:U\times V\to W$ tal que $\tilde f|_{B\times C}=f$.
Deduza que \[ \mbox{Func}(B\times C,W)\cong \mbox{Bil}(U\times V,W) \] onde o isomorfismo é entre espaços vetorias.

Exemplo 62.2 Para exemplificar o Exercício 62.2, seja $V=\R^n$ com a base canônica $e_1,\ldots,e_n$. Está bem conhecido que o produto interno $\langle \cdot,\cdot\rangle$ está determinado pelos valores de $\langle e_i,e_j\rangle$ com $i,j\in\{1,\ldots,n\}$. De fato, se $v,w\in\R^n$ (vetores linhas) e $v=(\alpha_1,\ldots,\alpha_n)$, $w=(\beta_1,\ldots,\beta_n)$, então \[ \langle v,w\rangle=\left\langle \sum_{i=1}^n\alpha_je_i,\sum_{j=1}^n\beta_j e_j\right\rangle=\sum_{i,j=1}^n\alpha_i\beta_j\langle e_i,e_j\rangle=\sum_{i=1}^n\alpha_i\beta_i. \] Ou seja, as igualdades $\langle e_i,e_j\rangle=\delta_{i,j}$ ($\delta$ de Kronecker) determinam o produto interno $\langle\cdot,\cdot\rangle$ completamente. Compare o argumento deste exemplo com Exemplo 47.2.

62.2 O produto tensorial

Definição 62.2 Um espaço vetorial $W$, juntamente com uma aplicação bilinear $\tau: U \times V \to W$, é chamado de produto tensorial de $U$ e $V$ (sobre $\F$) se satisfizer a seguinte propriedade universal: para qualquer espaço vetorial $Z$ e qualquer aplicação bilinear $f: U \times V \to Z$, existe um único homomorfismo linear $\tilde{f}: W \to Z$ tal que $f = \tilde{f} \circ \tau$. Ou seja, comuta o seguinte diagrama. [Diagrama do produto tensorial]

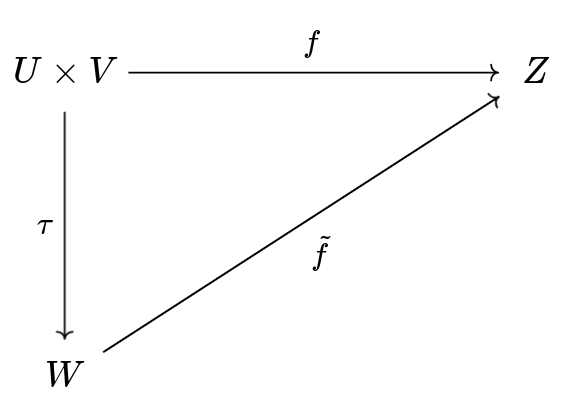
Da definição não fica imediatamente claro se o produto tensorial existe e, se sim, ele é único. Nos vamos responder estas duas perguntas no afirmativo.

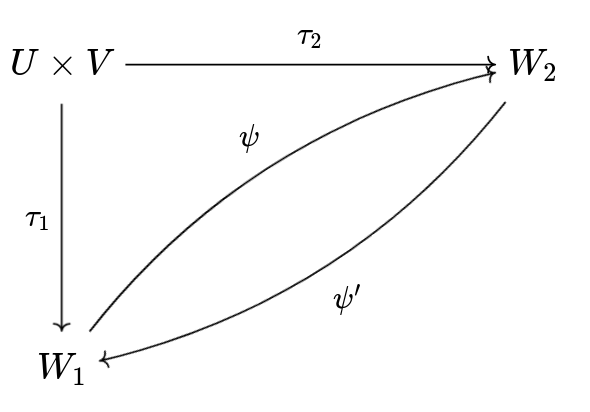
Teorema 62.1 Sejam $W_1$ e $W_2$ dois produtos tensoriais de $U$ e $V$, com aplicações bilineares associadas $\tau_1: U \times V \to W_1$ e $\tau_2: U \times V \to W_2$, respectivamente. Então, existe um isomorfismo linear único $\psi: W_1 \to W_2$ tal que $\psi \circ \tau_1 = \tau_2$.

Comprovação. Sejam $W_1$ e $W_2$ dois produtos tensoriais de $U$ e $V$ sobre $\F$, com as aplicações bilineares canônicas $\tau_1: U \times V \to W_1$ e $\tau_2: U \times V \to W_2$. Pela propriedade universal do produto tensorial $W_1$, existe um único homomorfismo linear $\psi: W_1 \to W_2$ tal que $\psi \circ \tau_1 = \tau_2$. Analogamente, pela propriedade universal do produto tensorial $W_2$, existe um único homomorfismo linear $\psi': W_2 \to W_1$ tal que $\psi' \circ \tau_2 = \tau_1$. Os homomorfismos estão ilustrados no seguinte diagrama.

Agora, considere o homomorfismo linear $\psi' \circ \psi: W_1 \to W_1$. Temos: \[ (\psi' \circ \psi) \circ \tau_1 = \psi' \circ (\psi \circ \tau_1) = \psi' \circ \tau_2 = \tau_1. \] Pela unicidade do homomorfismo linear garantida pela propriedade universal, segue que $\psi' \circ \psi$ é o homomorfismo identidade em $W_1$ como pode ser visto no seguinte diagrama.

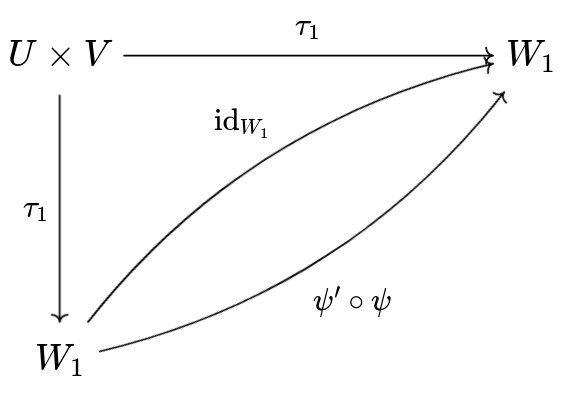
De maneira análoga, podemos mostrar que $\psi \circ \psi'$ é o homomorfismo identidade em $W_2$. Portanto, $\psi$ é um isomorfismo linear, e a unicidade de $\psi$ segue da propriedade universal do produto tensorial.

Assim, mostramos que existe um isomorfismo linear único $\psi: W_1 \to W_2$ tal que $\psi \circ \tau_1 = \tau_2$.

Se $W$ for um produto tensorial de $U$ e $V$ com aplicação bilinear canônica $\tau$, então, usando a unicidade de $W$ e $\tau$, o espaço $W$ será escrito como $U\otimes V$ e o elemento $\tau(u,v)$ será escrito como $u\otimes v$.

Corolário 62.1 Sejam $U,V,W$ $\F$-espaços vetoriais e sejam $B$ e $C$ bases de $U$ e $V$, respetivamente. Então os seguintes espaços são isomorfos: \[ \mbox{Bil}(U\times V,W)\cong \mbox{Func}(B\times C,W)\cong\mbox{Hom}(U\otimes V,W). \]

Exercício 62.3 Seja $X$ um conjunto qualquer e seja $\F$ um corpo. Defina $\F(X)$ como o conjunto das combinações lineares formais em $X$ com coeficientes em $\F$. Ou seja \[ \F(X)=\{\alpha_1x_1+\cdots+\alpha_kx_k\mid k\geq 0,\ \alpha_i\in\F,\ x_i\in X\}. \] A soma entre duas combinações formais \[ u=\alpha_1x_1+\cdots+\alpha_kx_k\quad\mbox{e}\quad v=\beta_1x_1+\cdots+\beta_kx_k \] é definida como \[ u+v=(\alpha_1+\beta_1)x_1+\cdots+(\alpha_k+\beta_k)x_k \] (permitindo que alguns coeficientes sejam nulos, pode assumir que os mesmos $x_i$ aparecem em $u$ e também em $v$). O múltiplo escalar é definido, para $\alpha\in\F$, como \[ \alpha v=\alpha\alpha_1 x_1+\cdots+\alpha\alpha_kv_k. \]

Demonstre que $\F(X)$ é um espaço vetorial.
Mostre que $X$ é uma base de $\F(X)$.
Demonstre que \[ \F(X)\cong\{f\in\mbox{Func}(X,\K)\mid f(x)=0\mbox{ exceto um número finito de valores $x$}\}. \]

Teorema 62.2 Para quaisquer espaços vetoriais $U$ e $V$ sobre $\F$, existe um produto tensorial $U \otimes V$ junto com a aplicação bilinear canônica $\tau: U \times V \to U \otimes V$ que satisfaz a propriedade universal do produto tensorial.

Comprovação. Considere o espaço vetorial $\F(U \times V)$, o espaço vetorial sobre $\F$ com base no conjunto $U \times V$. Os elementos de $\F(U \times V)$ são combinações lineares formais de pares $(u, v)$, onde $u \in U$ e $v \in V$. Definimos um subespaço $R \leq \F(U \times V)$ gerado pelas seguintes elementos:

$(u_1 + u_2, v) - (u_1, v) - (u_2, v)$ para todos $u_1, u_2 \in U$ e $v \in V$,
$(u, v_1 + v_2) - (u, v_1) - (u, v_2)$ para todos $u \in U$ e $v_1, v_2 \in V$,
$(\alpha u, v) - \alpha (u, v)$ para todos $u \in U$, $v \in V$ e $\alpha \in \F$,
$(u, \beta v) - \beta (u, v)$ para todos $u \in U$, $v \in V$ e $\beta \in \F$.

Definimos o espaço quociente $W = \F(U \times V) / R$. Denotamos a classe de equivalência de $(u, v)$ em $W$ por $u \otimes v$. A aplicação $\tau: U \times V \to W$ é definida por $\tau(u, v) = u \otimes v$. Por construção, $\tau$ é bilinear.

Agora, verificamos a propriedade universal. Seja $Z$ um espaço vetorial e $f: U \times V \to Z$ uma aplicação bilinear. Estendemos $f$ para uma aplicação linear $\tilde{f}: \F(U \times V) \to Z$. Como $f$ é bilinear, os geradores de $R$ são enviados a $0$ por $\tilde{f}$. Assim, $R \leq \ker(\tilde{f})$. Portanto, $\tilde{f}$ induz uma aplicação linear bem definida $\bar{f}: \F(U \times V) / R \to Z$ definida por \[ \bar f(u\otimes v)=\bar{f}((u, v)+R) = f(u, v), \] onde $(u, v) \in U \times V$.

Para mostrar que $\bar{f}$ é única, observe que $\bar f(u\otimes v)$ é determinado unicamente pelas condições do teorema, pois $\bar f(u\otimes v)=f(u,v)$ para todo $u\in U$ e $v\in V$. Como os elementos da forma $(u,v)$ geram $\F(U\times V)$, os elementos $u\otimes v$ geram $W$, e temos que $\bar f$ é determinado unicamente.

62.3 As propriedades básicas do produto tensorial

Teorema 62.3 Sejam $U$ e $V$ espaços vetoriais sobre $\F$, com bases $B$ e $C$, respectivamente. Então, o produto tensorial $U \otimes V$ tem como base o conjunto $\{b \otimes c \mid b\in B,\ c\in C\}$.

Comprovação. Seja $U \otimes V$ o produto tensorial de $U$ e $V$. Por definição, cada elemento de $U \otimes V$ pode ser escrito como uma combinação linear de elementos da forma $u \otimes v$, onde $u \in U$ e $v \in V$. Como $B$ e $C$ são bases de $U$ e $V$, respectivamente, podemos escrever $u = \sum_{i=1}^m \alpha_i b_i$ e $v = \sum_{j=1}^n \beta_j c_j$, com $b_i\in B$, $c_j\in C$, $\alpha_i, \beta_j \in \F$. Usando a bilinearidade do produto tensorial, temos: \[ u \otimes v = \left(\sum_{i=1}^m \alpha_i b_i\right) \otimes \left(\sum_{j=1}^n \beta_j c_j\right) = \sum_{i=1}^m \sum_{j=1}^n \alpha_i \beta_j (b_i \otimes c_j). \] Portanto, qualquer elemento de $U \otimes V$ pode ser escrito como uma combinação linear de elementos da forma $b_i \otimes c_j$, com $b_i \in B$ e $c_j \in C$. Isso implica que os elementos $b\otimes c$ com $b\in B$ e $c\in C$ geram $U\otimes V$.

Agora, mostramos que o conjunto $\{b \otimes c \mid b \in B,\ c \in C\}$ é linearmente independente. Suponha, por contradição, que existe $b_0\otimes c_0$ com $b_0\in B$ e $c_0\in C$ que pode ser escrito como uma combinação linear dos demais elementos de $\{b \otimes c \mid b\in B,\ c\in C\}$: \[ b_0\otimes c_0=\sum_{i=1}^m \sum_{j=1}^n \gamma_{ij} (b_i \otimes c_j); \] com $b_i\otimes b_j\neq b_0\otimes c_0$. Considere a aplicação $f_0:B\times C\to \F$ definida da seguinte forma \[ f_0(b, c)=\left\{\begin{array}{ll} 1 & \mbox {se $(b,c)=(b_0,c_0)$};\\ 0 & \mbox{caso contrário.}\end{array}\right. \] Então $f_0$ pode ser estendida a uma única aplicação bilinear $f:U\times V\to \F$. Pela propriedade universal do produto tensiorial, existe uma única aplicação linear $\bar f:U\otimes V\to \F$ tal que $\bar f(u\otimes v)=f(u,v)$ para $u\in U$ e $v\in V$. Em particular $\bar f(b,c)=f_0(b,c)$ para $b\in B$ e $c\in C$. Portanto, $\bar f(b_0\otimes c_0)=1$, mas \[ \bar f\left(\sum_{i=1}^m \sum_{j=1}^n \gamma_{ij} (b_i \otimes c_j)\right)=0. \] Mas isso é uma contradição.

Corolário 62.2 Sejam $U$ e $V$ espaços vetoriais sobre $\F$, com $\dim U = m$ e $\dim V = n$. Então, $\dim (U \otimes V) = m \cdot n$.

Comprovação. Sejam $B = \{b_1, b_2, \ldots, b_m\}$ e $C = \{c_1, c_2, \ldots, c_n\}$ bases de $U$ e $V$, respectivamente. Pelo teorema anterior, a base de $U \otimes V$ é dada por $\{b_i \otimes c_j \mid 1 \leq i \leq m, 1 \leq j \leq n\}$. O número de elementos dessa base é $m \cdot n$, pois há $m$ escolhas para $b_i$ e $n$ escolhas para $c_j$. Assim, $\dim (U \otimes V) = m \cdot n$.

Exercício 62.4 Sejam $U$ e $V$ espaços vetoriais e seja $B$ uma base de $V$. Demonstre que todo elemento de $U\otimes V$ pode ser escrito unicamente na forma \[ u_1\otimes b_1+\cdots+u_k\otimes b_k \] onde $u_i\in U$ e $b_i\in B$ e os $b_i$ são dois a dois distintos.

62.4 Transformações lineares do produto tensorial

Teorema 62.4 Sejam $f: U \to X$ e $g: V \to Y$ transformações lineares entre espaços vetoriais sobre $\F$. Então, existe uma transformação linear única $f \otimes g: U \otimes V \to X \otimes Y$ tal que $(f \otimes g)(u \otimes v) = f(u) \otimes g(v)$ para todos $u \in U$ e $v \in V$.

Comprovação. Sejam $f: U \to X$ e $g: V \to Y$ transformações lineares. Definimos uma aplicação bilinear $h: U \times V \to X \otimes Y$ por $h(u, v) = f(u) \otimes g(v)$ para todos $u \in U$ e $v \in V$. É fácil verificar que $h$ é bilinear. Pela propriedade universal do produto tensorial, existe uma transformação linear única $f \otimes g: U \otimes V \to X \otimes Y$ tal que $(f \otimes g)(u \otimes v) = h(u, v) = f(u) \otimes g(v)$ para todos $u \in U$ e $v \in V$.

62.5 Extensão do corpo base usando o produto tensorial

Sejam $\F$ e $\K$ corpos tais que $\F\subseteq \K$. Um $\K$-espaço pode ser considerado como um $\F$-espaço restringindo o múltiplo escalar para $\F$. Muitas vezes, nós queremos o contrário; ou seja, nós temos um $\F$-espaço $V$ que queremos considerar como um $\K$-espaço. Isso acontece frequentamente com $\R$-espaços. Por exemplo, Para garantir que um operador linear de um $\R$-espaço $V$ possui autovalor, consideramos $V$ como um $\C$-espaço.

Definição 62.3 Seja $V$ um espaço vetorial sobre um corpo $\F$, e seja $\K$ um corpo tal que $\F\subseteq \K$. Considere $\K$ como um $\F$-espaço vetorial. Definimos o $\K$-espaço $V_\K$ como $V_\K=\K\otimes V$. A soma neste espaço é a soma no produto tensorial $\K\otimes V$ e o múltiplo escalar é definido como \[ \lambda(\alpha\otimes v)=(\lambda\alpha)\otimes v. \] para $\lambda,\alpha\in\K$ e $v\in V$.

Definição 62.4 Demonstre que o múltiplo escalar em $V_\K$ está bem definido e $V_\K$ é um espaço vetorial sobre $\K$.

Teorema 62.5 Sejam $\F$, $\K$ e $V$ como na Definição 62.4. Se $B$ é uma base de $V$ sobre $\F$, então o conjunto $\{1 \otimes b \mid b \in B\}$ é uma base de $V_\K = \K \otimes V$ sobre $\K$.

Comprovação.

Geração: Seja $x \in V_\K$. Por definição do produto tensorial, $x$ pode ser escrito como uma combinação linear de elementos da forma $k \otimes v$, onde $k \in \K$ e $v \in V$. Como $B$ é uma base de $V$, podemos escrever $v = \sum_{i=1}^n \alpha_i b_i$ com $\alpha_i \in \F$ e $b_i\in B$. Assim, \[ k \otimes v = k \otimes \left(\sum_{i=1}^n \alpha_i b_i\right) = \sum_{i=1}^n k \alpha_i \otimes b_i=\sum_{i=1}^n k \alpha_i (1\otimes b_i). \] Note que $k \alpha_i \in \K$, pois $\F\subseteq \K$. Portanto, $x$ pode ser escrito como uma combinação linear de $\{1 \otimes b\mid b\in B\}$ com coeficientes em $\K$.
Independência linear: Suponha que $\sum_{i=1}^n k_i (1 \otimes b_i) = 0$ para alguns $k_i \in \K$ com $b_i\in B$. Isso implica que $\sum_{i=1}^n (k_i \otimes b_i) = 0$. Segue do Exercício 62.4 que isso é possível apenas quando $k_i=0$ para todo $i$. Assim, $\{1 \otimes b\mid b\in B\}$ é linearmente independente e o mesmo conjunto é uma base de $V_\K$.

Exemplo 62.3 Se $V$ é um $\R$-espaço vetorial, então $V_\C=\C\otimes V$ é um $\C$-espaço. Este espaço chama-se de complexificação de $V$. Por exemplo, os seguintes isomorfismos são válidos: \[\begin{align*} (\R^n)_{\C}&\cong\C^n;\\ \mbox{Mat}_{m\times n}(\R)_\C&\cong\mbox{Mat}_{m\times n}(\C);\\ \R[x]_\C&\cong\C[x]. \end{align*}\]

62.6 O produdo tensorial de vários espaços

O produto tensorial $V_1\otimes\cdots\otimes V_k$ pode ser definida também para vários fatores $V_1,\ldots,V_k$. Isso seria possível, por um lado, obsevando que o produto tensorial é associativo; ou seja, $(V_1\otimes V_2)\otimes V_3 \cong V_1\otimes(V_2\otimes V_3)$ (demonstre isso). Para nós, vai ser mais oportuno definir o produto com vários fatores via a propriedade universal. Nesta seção, nós revisamos a construção com as propriedades principais. Como as demonstrações são similares às demonstrações em cima para $U\otimes V$, elas serão omitidas.

Definição 62.5 Sejam $V$ e $W$ espaços vetoriais sobre $\F$, $k\geq 1$, e considere o produto cartesiano $V^k=V\times \cdots\times V$ de $k$ cópias de $V$. Dizemos que uma aplicação $f:V^k\to W$ é $k$-linear se ela é linear em todas as variáveis. Em outras palávras, \[ f(v_1,\ldots,\alpha v_i+\beta w,\ldots v_k)=\alpha f(v_1,\ldots,v_i,\ldots v_k)+\beta f(v_1,\ldots,w,\ldots v_k) \] vale para todo $i\in\{1,\ldots,k\}$, $v_i\in V$ e $w\in V$. Uma aplicação $V^k\to \F$ $k$-linear é chamada de forma (ou funcional) $k$-linear.

Exemplo 62.4 Uma forma $1$-linear é simplesmente uma forma linear $V\to \F$. Uma aplicação ou forma $2$-linear é frequentemente chamada de bilinear, enquanto uma aplicação ou forma $3$-linear é chamada de trilinear.

Se $V=\R^n$, então o produto interno $\langle\cdot ,\cdot\rangle$ é bilinear. Por outro lado, se $V=\C^n$, então o produto interno $\langle\cdot ,\cdot\rangle$ não é bilinear (porque?, consulte a Definição 73.2). Se $V=\F^n$, então a aplicação \[ d:V^n\to \F,\quad d(a_1,\ldots,a_n)=\det A, \] onde $A$ é a matriz formada pelas linhas $a_1,\ldots,a_n$, é $n$-linear.

Definição 62.6 Sejam $V_1, V_2, \ldots, V_k$ espaços vetoriais sobre um corpo $\F$. Um espaço vetorial $W$, juntamente com uma aplicação multilinear $\tau: V_1 \times V_2 \times \cdots \times V_k \to W$, é chamado de produto tensorial de $V_1, V_2, \ldots, V_k$ (sobre $\F$) se satisfizer a seguinte propriedade universal: para qualquer espaço vetorial $Z$ e qualquer aplicação multilinear $f: V_1 \times V_2 \times \cdots \times V_k \to Z$, existe um único homomorfismo linear $\tilde{f}: W \to Z$ tal que $f = \tilde{f} \circ \tau$.

Teorema 62.6 Para quaisquer espaços vetoriais $V_1, V_2, \ldots, V_k$ sobre $\F$, existe um produto tensorial $W_1$ juntamente com uma aplicação multilinear canônica $\tau_1: V_1 \times V_2 \times \cdots \times V_k \to W_1$ que satisfaz a propriedade universal do produto tensorial. Além disso, o produto tensorial é único no seguinte sentido: se $W_2$ é outro espaço vetorial com uma aplicação multilinear $\tau_2: V_1 \times V_2 \times \cdots \times V_k \to W_2$ que satisfaz a propriedade universal, então existe um isomorfismo linear único $\psi: W_1 \to W_2$ tal que $\psi \circ \tau_1 = \tau_2$.

Pela unicidade do produto tensorial, ele vai ser denotado por $V_1\otimes\cdots\otimes V_k$ e $\tau(v_1,\ldots,v_k)$ será escrito como $v_1\otimes\cdots\otimes v_k$.

Teorema 62.7 Sejam $V_1, V_2, \ldots, V_k$ e $Z$ espaços vetoriais sobre um corpo $\F$, e sejam $B_1, B_2, \ldots, B_k$ bases de $V_1, V_2, \ldots, V_k$, respectivamente. Então, os seguintes espaços são isomorfos: \[ \mbox{Func}(B_1 \times B_2 \times \cdots \times B_k, Z) \cong \mbox{MLin}(V_1 \times V_2 \times \cdots \times V_k, Z) \cong \mbox{Hom}(V_1 \otimes V_2 \otimes \cdots \otimes V_k, Z), \] onde $\mbox{Func}(B_1 \times B_2 \times \cdots \times B_k, Z)$ denota o espaço de todas as funções de $B_1 \times B_2 \times \cdots \times B_k$ em $Z$, $\mbox{MLin}(V_1 \times V_2 \times \cdots \times V_k, Z)$ denota o espaço de todas as aplicações multilineares de $V_1 \times V_2 \times \cdots \times V_k$ em $Z$, e $\mbox{Hom}(V_1 \otimes V_2 \otimes \cdots \otimes V_k, Z)$ denota o espaço de todos os homomorfismos lineares de $V_1 \otimes V_2 \otimes \cdots \otimes V_k$ em $Z$.

Teorema 62.8 Sejam $V_1, V_2, \ldots, V_k$ espaços vetoriais sobre $\F$, com bases $B_1, B_2, \ldots, B_k$, respectivamente. Então, o produto tensorial $V_1 \otimes V_2 \otimes \cdots \otimes V_k$ tem como base o conjunto \[ \{b_1 \otimes b_2 \otimes \cdots \otimes b_k \mid b_i \in B_i \text{ para } i = 1, 2, \ldots, k\}. \]

Corolário 62.3 Sejam $V_1, V_2, \ldots, V_k$ espaços vetoriais sobre $\F$, com $\dim V_i = n_i$ para $i = 1, 2, \ldots, k$. Então, \[ \dim (V_1 \otimes V_2 \otimes \cdots \otimes V_k) = n_1 \cdot n_2 \cdot \cdots \cdot n_k. \]

Teorema 62.9 Sejam $f_i: V_i \to W_i$ transformações lineares entre espaços vetoriais sobre $\F$ para $i = 1, 2, \ldots, k$. Então, existe uma transformação linear única \[ f_1 \otimes f_2 \otimes \cdots \otimes f_k: V_1 \otimes V_2 \otimes \cdots \otimes V_k \to W_1 \otimes W_2 \otimes \cdots \otimes W_k \] tal que \[ (f_1 \otimes f_2 \otimes \cdots \otimes f_k)(v_1 \otimes v_2 \otimes \cdots \otimes v_k) = f_1(v_1) \otimes f_2(v_2) \otimes \cdots \otimes f_k(v_k) \] para todos $v_i \in V_i$.