49 Ângulos e ortogonalidade

49.1 A definição do ângulo

Seja \(V\) um espaço vetorial com produto interno. Se lembre que o gráfico de \(\tn{cos}(\theta)\) entre \(0\) e \(\pi\) é:

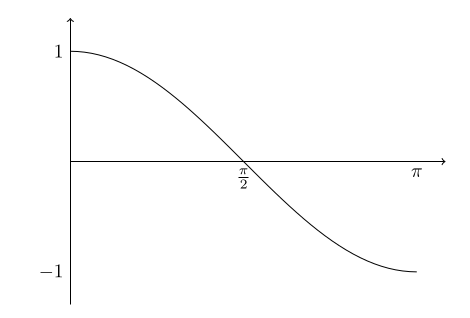
A desigualdade de Cauchy-Schwarz nos diz que para quaisquer vetores não nulos \(\ul{u},\ul{v}\), temos \[-1\leqslant \frac{\langle\ul{u},\ul{v}\rangle}{\|\ul{u}\|\cdot\|\ul{v}\|} \leqslant 1.\] Segue que para qualquer par de vetores \(\ul{u}, \ul{v}\) não nulos, existe um único número \(\theta\in [0,\pi]\) tal que \[\tn{cos}(\theta) = \frac{\langle\ul{u},\ul{v}\rangle}{\|\ul{u}\|\cdot\|\ul{v}\|}.\]

Definição 49.1 Sejam \(V\) um espaço vetorial com produto interno e \(\ul{u}, \ul{v}\) vetores não nulos de \(V\). O ângulo entre \(\ul{u}\) e \(\ul{v}\) é o número \(\theta\in [0,\pi]\) tal que \[\tn{cos}(\theta) = \frac{\langle\ul{u},\ul{v}\rangle}{\|\ul{u}\|\cdot\|\ul{v}\|}.\]

Exemplo 49.1 Considere o espaço \(\R^2\) com produto interno normal. Vamos calcular o ângulo \(\theta\) entre \((2,1)\) e \((-1,2)\):

\[\tn{cos}(\theta) = \frac{(2,1)\cdot(-1,2)}{\|(2,1)\|\cdot\|(-1,2)\|} = \frac{0}{\sqrt{5}\cdot\sqrt{5}} = 0.\] Logo \(\theta = \cos^{-1}(0) = \ul{\ul{\pi/2}} \,(= 90^{\textnormal{o}})\).

Mas o ângulo também depende do produto interno! Pegando os mesmos vetores em \(\R^2\) mas agora com respeito ao produto interno dado pela matriz \[A = \begin{pmatrix} 2 & -1 \\ -1 & 2 \end{pmatrix},\] temos \[\tn{cos}(\theta) = \frac{\langle(2,1),(-1,2)\rangle_A}{\|(2,1)\|\cdot\|(-1,2)\|} = \frac{-3}{\sqrt{6}\cdot\sqrt{14}} \approx -0,33.\] Então \[\theta \approx \cos^{-1}(-0,33) \approx 1,907\, > \pi/2.\]

Definição 49.2 Sejam \(V\) um espaço vetorial com produto interno e \(\ul{u}, \ul{v}\) vetores não nulos de \(V\). Diremos que \(\ul{u}, \ul{v}\) são ortogonais (ou perpendiculares) se \(\langle \ul{u},\ul{v}\rangle = 0\). Neste caso, escrevemos \(\ul{u}\perp \ul{v}\).

Seja \(\theta\) o ângulo entre \(\ul{u},\ul{v}\neq \ul{0}\). Observe que \[\ul{u}\perp \ul{v}\Longleftrightarrow \langle \ul{u},\ul{v}\rangle = 0 \Longleftrightarrow \frac{\langle \ul{u},\ul{v}\rangle}{\|\ul{u}\|\cdot\|\ul{v}\|} = 0 \Longleftrightarrow \cos(\theta) = 0 \Longleftrightarrow \theta = \pi/2.\]

Exemplo 49.2 Já calculamos que \((2,1), (-1,2)\) são ortogonais com respeito ao produto interno normal de \(\R^2\), pois \[(2,1)\cdot (-1,2) = -2 + 2 = 0.\] Mas eles não são ortogonais com respeito ao outro produto \(\langle-,-\rangle_A\) que estamos usando, pois \(\langle (2,1),(-1,2)\rangle_A = -3\neq 0\).

Vamos calcular os vetores \((x,y)\) perpendiculares ao vetor \((2,1)\) com respeito ao produto \(\langle-,-\rangle_A\): \[\langle(2,1),(x,y)\rangle_A = \begin{pmatrix}2 & 1\end{pmatrix}\begin{pmatrix}2 & -1 \\ -1 & 2\end{pmatrix}\begin{pmatrix}x \\ y\end{pmatrix} = \begin{pmatrix}3 & 0\end{pmatrix}\begin{pmatrix}x \\ y\end{pmatrix} = 3x.\] Logo \((x,y)\) é ortogonal a \((2,1)\) se, e somente se, \(x=0\). Por exemplo, os vetores \[(2,1)\,,\,(0,1)\] são ortogonais com respeito a esse produto interno.

49.2 Projeção ortogonal

Seja \(V\) um espaço vetorial de dimensão finita com produto interno \(\langle-,-\rangle\). Temos as ferramentas para nomear as melhores bases de \(V\):

Definição 49.3 Uma base \(B\) de \(V\) é ortogonal se \(\langle\ul{b},\ul{c}\rangle = 0\) para quaisquer \(\ul{b}\neq \ul{c}\) em \(B\). A base é ortonormal se ela é ortogonal e se todo \(\ul{b}\in B\) tem norma \(1\).

Exemplo 49.3

A base canônica de \(\R^n\) é ortonormal com respeito ao produto interno normal [Confirme isso!].
Já vimos que os vetores \((2,1)\) e \((0,1)\) são ortogonais com respeito a nosso produto interno \(\langle-,-\rangle_A\). Eles são LI, então formam uma base ortogonal de \(\R^2\) com este produto interno. As suas normas são: \[\|(2,1)\| = \sqrt{\begin{pmatrix}2 & 1 \end{pmatrix}\begin{pmatrix}2 & -1 \\ -1 & 2 \end{pmatrix}\begin{pmatrix}2 \\ 1 \end{pmatrix}} = \sqrt{\begin{pmatrix}2 & 1 \end{pmatrix}\begin{pmatrix}3 \\ 0 \end{pmatrix}} = \sqrt{6}\] e \[\|(0,1)\| = \sqrt{\begin{pmatrix}0 & 1 \end{pmatrix}\begin{pmatrix}2 & -1 \\ -1 & 2 \end{pmatrix}\begin{pmatrix}0 \\ 1 \end{pmatrix}} = \sqrt{\begin{pmatrix}0 & 1 \end{pmatrix}\begin{pmatrix}-1 \\ 2 \end{pmatrix}} = \sqrt{2},\] então os vetores \(\frac{1}{\sqrt{6}}(2,1)\) e \(\frac{1}{\sqrt{2}}(0,1)\) são unitários. Segue que \[(2/\sqrt{6}\,,\,1/\sqrt{6})\quad,\quad (0\,,\, 1/\sqrt{2})\] é uma base ortonormal de \(\R^2\) com respeito a este produto interno.

Pelo resto dessa seção, seja \(V\) um espaço vetorial de dimensão finita \(n\) com produto interno. Vamos mostrar que \(V\) possui uma base ortonormal.

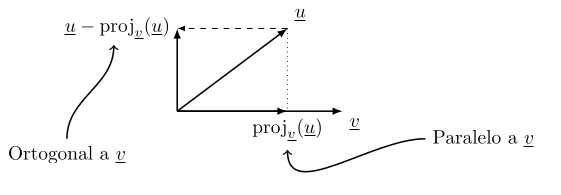
Proposição 49.1 Sejam \(\ul{u}, \ul{v}\) vetores LI de \(V\). Existe um único vetor \(\tn{proj}_{\ul{v}}(\ul{u})\), chamado projeção ortogonal de \(\ul{u}\) sobre \(\ul{v}\) com as propriedades que

\(\tn{proj}_{\ul{v}}(u)\) é múltiplo escalar de \(\ul{v}\) (ou seja, \(\tn{proj}_{\ul{v}}(\ul{u})\) e \(\ul{v}\) são paralelos)
\(\ul{u} - \tn{proj}_{\ul{v}}(\ul{u})\) e \(\ul{v}\) são ortogonais.

De fato, \[\tn{proj}_{\ul{v}}(\ul{u}) = \left(\frac{\langle\ul{u},\ul{v}\rangle}{\|\ul{v}\|^2}\right)\ul{v}.\]

Comprovação. de \(\ul{v}\) por definição. Temos \[\langle \ul{u} - \tn{proj}_{\ul{v}}(\ul{u})\,,\, \ul{v}\rangle = \langle \ul{u},\ul{v}\rangle - \frac{\langle\ul{u},\ul{v}\rangle}{\|\ul{v}\|^2}\cdot \langle \ul{v},\ul{v}\rangle = 0.\quad\checkmark\] Exercício: confirme que ele é único. Qualquer outro vetor com as propriedades tem a forma \(\alpha \ul{v}\) para algum \(\alpha\in \R\). Mostre que \(\alpha = \frac{\langle\ul{u},\ul{v}\rangle}{\|\ul{v}\|^2}\). ◻

Com respeito ao produto interno normal de \(\R^n\), podemos visualizar a projeção ortogonal assim:

49.3 Bases ortogonais e ortonormais

Teorema 49.1

Seja \(W\) um subespaço de \(V\) e suponha que \(W\) possui base ortogonal \(B = \{\ul{w_1},\ldots,\ul{w_s}\}\). Podemos estender \(B\) para uma base ortogonal de \(V\).
\(V\) possui uma base ortonormal.

Comprovação.

Trabalhamos por indução sobre \(n-s\). Caso \(n-s = 0\), então \(W = V\) e já temos uma base ortogonal (\(B\)) de \(V\). Suponha que o resultado vale para qualquer \(k\) com \(n-k\) menor do que \(n-s\). Pegue um vetor \(\ul{u}\) de \(V\) que não pertence a \(W\). Queremos manipular \(\ul{u}\) para um vetor perpendicular a cada \(\ul{w_i}\). Afirmo que \[\ul{w_{s+1}} = \ul{u} - \tn{proj}_{\ul{w_1}}(\ul{u}) - \cdots - \tn{proj}_{\ul{w_s}}(\ul{u})\] serve. Primeiro, observe que \(\tn{proj}_{\ul{w_i}}(\ul{u})\) é um múltiplo escalar de \(\ul{w_i}\), logo \(\ul{w_{s+1}}\) é uma combinação linear não nula do conjunto LI \(\{\ul{u},\ul{w_1},\ldots,\ul{w_s}\}\), logo \(\ul{w_{s+1}}\neq \ul{0}\).

Para cada \(i\), temos
\[\begin{aligned} \langle \ul{w_{s+1}},\ul{w_i}\rangle & = \langle \ul{u},\ul{w_i}\rangle - \langle \tn{proj}_{\ul{w_1}}(\ul{u}),\ul{w_i}\rangle - \cdots - \langle \tn{proj}_{\ul{w_s}}(\ul{u}),\ul{w_i}\rangle \\ & = \langle \ul{u},\ul{w_i}\rangle - 0 - \cdots - 0 - \langle \tn{proj}_{\ul{w_i}}(\ul{u}),\ul{w_i}\rangle - 0 - \cdots - 0 \\ & = \langle \ul{u},\ul{w_i}\rangle - \langle \tn{proj}_{\ul{w_i}}(\ul{u}),\ul{w_i}\rangle \\ & = \langle \ul{u} - \tn{proj}_{\ul{w_i}}(\ul{u}),\ul{w_i}\rangle \\ & = 0.\qquad\checkmark \end{aligned}\]
Agora, o subespaço com base ortogonal \(B\cup\{\ul{w_{s+1}}\}\) satisfaz as condições do teorema e tem dimensão \(s+1\). Já que \(n-(s+1) < n-s\), pela hipótese de indução, podemos estender a base \(B\cup \{\ul{w_{s+1}}\}\) para uma base ortogonal de \(V\).
Começando com o subconjunto vazio \(\varnothing\) de \(V\), aplique o processo da primeira parte \(n\) vezes para obter uma base ortogonal de \(V\). Depois simplesmente multiplique cada vetor \(\ul{w}\) em nossa base ortogonal pelo número \(\frac{1}{\|\ul{w}\|}\) para obter uma base ortonormal de \(V\).

◻

Observação: O processo de estender uma base ortogonal de um subespaço para uma base ortogonal maior como na prova deste teorema se chama o processo de ortogonalizaçaõ de Gram-Schmidt.

Exemplo 49.4 Vamos usar Gram-Schmidt para achar mais uma base ortonormal de \(\R^2\) com o produto interno \(\langle-,-\rangle_A\) dado pela matriz \[A = \begin{pmatrix}2 & -1 \\ -1 & 2\end{pmatrix}.\] Começa com o vetor \(\ul{w_1} = (1,0)\). Depois, pegamos um vetor \(\ul{u}\) qualquer com \(\{\ul{u},\ul{w_1}\}\) LI. Vamos pegar \((0,2)\). Seguindo o processo, \[\begin{aligned} \ul{w_2} & = \ul{u} - \tn{proj}_{\ul{w_1}}(\ul{u}) \\ & = (0,2) - \left(\frac{\langle(0,2),(1,0)\rangle_A}{\|(1,0)\|^2}\right)(1,0) \\ & = (0,2) - \left(\frac{\begin{pmatrix}0 & 2\end{pmatrix}\begin{pmatrix}2 & -1 \\ -1 & 2 \end{pmatrix}\begin{pmatrix}1 \\ 0\end{pmatrix}}{\begin{pmatrix}1 & 0\end{pmatrix}\begin{pmatrix}2 & -1 \\ -1 & 2 \end{pmatrix}\begin{pmatrix}1 \\ 0\end{pmatrix}}\right)(1,0) \\ & = (0,2) - \left(\frac{-2}{2}\right)(1,0) \\ & = (0,2) + (1,0) \\ & = (1,2). \end{aligned}\] Vamos confirmar que \((1,0)\) e \((1,2)\) são ortogonais: \[\langle(1,0),(1,2)\rangle_A = \begin{pmatrix}1 & 0\end{pmatrix}\begin{pmatrix}2 & -1 \\ -1 & 2 \end{pmatrix}\begin{pmatrix}1 \\ 2\end{pmatrix} = \begin{pmatrix}1 & 0\end{pmatrix}\begin{pmatrix}0 \\ 3\end{pmatrix} = 0.\quad\checkmark\] Pra base \(\{\ul{w_1}, \ul{w_2}\} = \{(1,0),(1,2)\}\) ser ortonormal, temos que dividir pelas normas: \[\|(1,0)\| = \sqrt{\begin{pmatrix}1 & 0 \end{pmatrix}\begin{pmatrix}2 & -1 \\ -1 & 2 \end{pmatrix}\begin{pmatrix}1 \\ 0 \end{pmatrix}} = \sqrt{2}.\] \[\|(1,2)\| = \sqrt{\begin{pmatrix}1 & 2 \end{pmatrix}\begin{pmatrix}2 & -1 \\ -1 & 2 \end{pmatrix}\begin{pmatrix}1 \\ 2 \end{pmatrix}} = \sqrt{6}.\] Obtemos assim a base ortonormal \[\{(1/\sqrt{2}\,,\,0)\,,\,(1/\sqrt{6}\,,\,2/\sqrt{6})\}.\]

Uma propaganda para bases ortogonais/ortonormais: dado um vetor \(\ul{v}\), é fácil escrever ele como combinação linear dos elementos de uma base ortogonal:

Proposição 49.2 Seja \(B\) uma base ortogonal de \(V\) e seja \(\ul{v}\) um vetor de \(V\). Então \[\ul{v} = \sum_{\ul{b}\in B}\frac{\langle\ul{v},\ul{b}\rangle}{\,\,\|\ul{b}\|^2}\,\ul{b}.\] Caso a base \(B\) for ortonormal, então \[\ul{v} = \sum_{\ul{b}\in B}\langle\ul{v},\ul{b}\rangle\,\ul{b}.\]

Comprovação. \(\ul{v} = \lambda_1\ul{b_1}+\cdots+\lambda_n\ul{b_n}\) para alguns \(\ul{b_i}\in B\) e \(\lambda_i\in \R\). Vamos calcular \(\lambda_i\): \[\begin{aligned} \langle \ul{v}, \ul{b_i}\rangle = & \langle \lambda_1\ul{b_1}+\cdots+\lambda_n\ul{b_n},\ul{b_i}\rangle \\ = & \sum \lambda_j\langle \ul{b_j},\ul{b_i}\rangle \\ = & \lambda_i \langle \ul{b_i},\ul{b_i}\rangle\qquad (\hbox{pois base ortogonal}). \end{aligned}\] Logo \[\lambda_i = \frac{\langle\ul{v},\ul{b_i}\rangle}{\langle \ul{b_i},\ul{b_i}\rangle} = \frac{\langle\ul{v},\ul{b_i}\rangle}{\,\,\|\ul{b_i}\|^2}.\qquad \checkmark\] A segunda afirmação segue pois \(B\) ortonormal implica que \(\langle \ul{b_i},\ul{b_i}\rangle = 1\) para cada \(i\). ◻

Exemplo 49.5 No espaço \(\R^2\) com produto interno dado pela matriz \(\begin{pmatrix}2 & -1 \\ -1 & 2\end{pmatrix}\), já temos a base ortonormal \[B = \{(1/\sqrt{2}, 0)\,,\,(1/\sqrt{6}, 2/\sqrt{6})\}.\] Vamos calcular o vetor de coordenadas com respeito à base \(B\) do vetor \((\sqrt{6}, \sqrt{6})\): Pela proposição, \[(\sqrt{6},\sqrt{6}) = \lambda (1/\sqrt{2},0) + \mu (1/\sqrt{6},2/\sqrt{6}),\] em que \[\lambda = \langle(\sqrt{6},\sqrt{6}),(1/\sqrt{2},0)\rangle_A = \begin{pmatrix}\sqrt{6} & \sqrt{6}\end{pmatrix}\begin{pmatrix}2 & -1 \\ -1 & 2\end{pmatrix}\begin{pmatrix}1/\sqrt{2} \\ 0\end{pmatrix} = \sqrt{3},\] \[\mu = \langle(\sqrt{6},\sqrt{6}),(1/\sqrt{6},2/\sqrt{6})\rangle_A = \begin{pmatrix}\sqrt{6} & \sqrt{6}\end{pmatrix}\begin{pmatrix}2 & -1 \\ -1 & 2\end{pmatrix}\begin{pmatrix}1/\sqrt{6} \\ 2/\sqrt{6}\end{pmatrix} = 3.\] Logo, o vetor de coordenadas de \((\sqrt{6},\sqrt{6})\) com respeito à base \(B\) é \[\begin{pmatrix}\sqrt{3} \\ 3\end{pmatrix}.\] Vamos só confirmar: \[\sqrt{3}\begin{pmatrix}1/\sqrt{2} \\ 0\end{pmatrix} + 3\begin{pmatrix}1/\sqrt{6} \\ 2/\sqrt{6}\end{pmatrix} = \begin{pmatrix}\sqrt{3}/\sqrt{2}+3/\sqrt{6} \\ 6/\sqrt{6}\end{pmatrix} = \begin{pmatrix}\sqrt{6} \\ \sqrt{6}\end{pmatrix}.\quad\checkmark\]

Fim da propaganda.

49.4 Complemento ortogonal

Dado um subespaço \(W\) de \(V\), sabemos que existem muitos complementos de \(W\) em \(V\). Isto é, subespaços \(Y\) de \(V\) tais que \(V = W\oplus Y\). Mas existe um complemento especial:

Definição 49.4 Seja \(W\) um subespaço de \(V\). O complemento ortogonal de \(W\) em \(V\) é \[W^{\perp} = \{\ul{v}\in V\,|\, \langle \ul{v},\ul{w}\rangle = 0\,\,\forall \ul{w}\in W\}.\]

Proposição 49.3 Seja \(V\) um espaço vetorial de dimensão finita e \(W\) um subespaço de \(V\).

\(W^{\perp}\) é subespaço de \(V\),
\(V = W \oplus W^{\perp}\),
\((W^{\perp})^{\perp} = W\).
Se \(B\) é base ortogonal de \(W\) e \(C\) é base ortogonal de \(W^{\perp}\), então \(B\cup C\) é base ortogonal de \(V\).

Comprovação.

\(\langle \ul{0},\ul{w}\rangle = 0\) para qualquer \(\ul{w}\), logo \(\ul{0}\in W^{\perp}\). Se \(\ul{u},\ul{v}\in W^{\perp}\) então para qualquer \(\ul{w}\in W\), temos \[\langle\ul{u}+\ul{v},\ul{w}\rangle = \langle \ul{u},\ul{w}\rangle + \langle \ul{v},\ul{w}\rangle = 0 + 0 = 0.\quad\checkmark\] Similarmente, \(\ul{u}\in W^{\perp} \implies \lambda \ul{u}\in W^{\perp}\,\forall \lambda\in \R\).

Prova alternativa disso: \(\langle -,-\rangle\) é bilinear, logo \(\langle -,\ul{w}\rangle\) é uma TL para cada \(\ul{w}\in W\). Já que \[W^{\perp} = \bigcap_{\ul{w}\in W}\tn{Ker}\left(\langle-,\ul{w}\rangle\right)\] é uma interseção de subespaços de \(V\), ele é um subespaço.
Seja \(B = \{\ul{w_1},\ldots,\ul{w_s}\}\) uma base ortogonal de \(W\) e, pela proposição anterior, estenda \(B\) para uma base ortogonal \[\{\ul{w_1},\ldots,\ul{w_s},\ul{v_1},\ldots,\ul{v_t}\}\] de \(V\). Considere \(C = \{\ul{v_1},\ldots,\ul{v_t}\}\). Já que cada \(\ul{v_i}\) é ortogonal a cada \(\ul{w_j}\), segue que qualquer combinação linear dos \(\ul{v_i}\) é ortogonal a qualquer combinação linear dos \(\ul{w_j}\). Logo, o subespaço gerado por \(C\) está contido em \(W^{\perp}\), e assim \[W + W^{\perp}\geqslant W + [C] = V.\] Falta confirmar que \(W\cap W^{\perp} = \{\ul{0}\}\), mas pegue \(\ul{w}\in W\cap W^{\perp}\). Segue pela definição de \(W^{\perp}\) que \(\langle \ul{w}, \ul{w}\rangle = 0\), e logo que \(\ul{w} = \ul{0}\), já que produtos internos são positivo definidos.
Seja \(\ul{w}\in W\). Para qualquer \(\ul{v}\in W^{\perp}\), temos \[0 = \langle\ul{v},\ul{w}\rangle = \langle \ul{w},\ul{v}\rangle,\] mostrando que \(\ul{w}\in (W^{\perp})^{\perp}\).

Na outra direção, pegue \(\ul{x}\in (W^{\perp})^{\perp}\). Já que \(V = W \oplus W^{\perp}\), escreva \(\ul{x} = \ul{w} + \ul{v}\) com \(\ul{w}\in W, \ul{v}\in W^{\perp}\). Queremos mostrar que \(\ul{v} = \ul{0}\). Mas \[0 =\langle \ul{v},\ul{x}\rangle = \langle \ul{v},\ul{w}\rangle + \langle \ul{v},\ul{v}\rangle = 0 + \langle \ul{v},\ul{v}\rangle.\] Já que o produto é positivo definido, segue que \(\ul{v} = \ul{0}\). Logo \(\ul{x} = \ul{w}\in W\), como queríamos mostrar.
Exercício.

◻

Exemplo 49.6 Considere \(\R^3\) com o produto interno normal. Seja \(W\) o subespaço gerado pelos vetores \((1,0,1)\) e \((2,2,2)\). Vamos encontrar uma base ortogonal \(\{\ul{w_1},\ul{w_2}\}\) de \(W\) usando o processo de Gram-Schmidt: \[\ul{w_1} = (1,0,1).\] \[\begin{aligned} \ul{w_2} & = (2,2,2) - \left(\frac{(2,2,2)\cdot (1,0,1)}{\|(1,0,1)\|^2}\right)(1,0,1) \\ & = (2,2,2) - 2(1,0,1) \\ & = (2,2,2) - (2,0,2) \\ & = (0,2,0). \end{aligned}\] O complemento ortogonal \(W^{\perp}\) tem dimensão \(3-2 = 1\) pela proposição, então é gerado por qualquer vetor ortogonal a \(\ul{w_1}\) e \(\ul{w_2}\). O vetor \((1,0,0)\) não pertence a \(W\). Usando Gram-Schmidt de novo, o vetor \[\begin{aligned} \ul{v} & = (1,0,0) - \left(\frac{(1,0,0)\cdot (1,0,1)}{\|(1,0,1)\|^2}\right)(1,0,1) - \left(\frac{(1,0,0)\cdot (0,2,0)}{\|(0,2,0)\|^2}\right)(0,2,0) \\ & = (1,0,0) - \frac{1}{2}(1,0,1) - \frac{0}{4}(0,2,0) \\ & = (1,0,0) - (1/2,0,1/2) \\ & = (1/2,0,-1/2) \end{aligned}\] gera o complemento ortogonal de \(W\).

Exemplo 49.7 Vamos calcular uma base ortogonal para o espaço vetorial dos polinômios de grau no máximo 2, com o produto interno dado por \[\langle f, g \rangle = \int_0^1 f(x)g(x) \, dx.\]

Começamos com a base padrão \(\{1, x, x^2\}\) e aplicamos o processo de Gram-Schmidt.

Primeiro vetor ortogonal: \[\ul{p_1}(x) = 1.\]
Segundo vetor ortogonal: \[\ul{p_2}(x) = x - \frac{\langle x, 1 \rangle}{\langle 1, 1 \rangle} \cdot 1 = x - \int_0^1 x \, dx = x - \frac{1}{2}.\]
Terceiro vetor ortogonal: \[\begin{aligned} \ul{p_3}(x) & = x^2 - \frac{\langle x^2, 1 \rangle}{\langle 1, 1 \rangle} \cdot 1 - \frac{\langle x^2, x - \frac{1}{2} \rangle}{\langle x - \frac{1}{2}, x - \frac{1}{2} \rangle} \cdot \left( x - \frac{1}{2} \right) \\ & = x^2 - \int_0^1 x^2 \, dx - \frac{\int_0^1 x^2 \left( x - \frac{1}{2} \right) \, dx}{\int_0^1 \left( x - \frac{1}{2} \right)^2 \, dx} \cdot \left( x - \frac{1}{2} \right) \\ & = x^2 - \frac{1}{3} - \frac{\int_0^1 x^3 - \frac{1}{2}x^2 \, dx}{\int_0^1 x^2 - x + \frac{1}{4} \, dx} \cdot \left( x - \frac{1}{2} \right) \\ & = x^2 - \frac{1}{3} - \frac{\left( \frac{1}{4} - \frac{1}{6} \right)}{\left( \frac{1}{3} - \frac{1}{2} + \frac{1}{4} \right)} \cdot \left( x - \frac{1}{2} \right) \\ & = x^2 - \frac{1}{3} - \frac{\frac{1}{12}}{\frac{1}{12}} \cdot \left( x - \frac{1}{2} \right) \\ & = x^2 - \frac{1}{3} - \left( x - \frac{1}{2} \right) \\ & = x^2 - x + \frac{1}{6}. \end{aligned}\]

Portanto, a base ortogonal é \(\{1, x - \frac{1}{2}, x^2 - x + \frac{1}{6}\}\).