3  Listas, matrizes e permutações

Nesta página, vamos ver como trabalhar com listas, matrizes e permutações em GAP.

3.1 Listas

Listas são importantes em GAP (manual). Listas contém uma sequência de objetos. Os objetos nas listas podem ser números, carateres, ou até objetos complexos, tais como grupos, subgrupos de um grupo, etc. Os seguintes exemplos mostram a criação de listas e as operações básicas com listas.

gap> L := [1..10]
[ 1 .. 10 ]
gap> L1 := [1,3,5,7,9,10,8,6,4,2,0];
[ 1, 3, 5, 7, 9, 10, 8, 6, 4, 2, 0 ]
gap> L2 := ["a","b","c","z","x","y"];
[ "a", "b", "c", "z", "x", "y" ]

Para acessar os elementos de uma lista, usamos list[n] que devolve o \(n\)-ésimo elemento começando por list[1]. Para verificar se um objeto pertence ou não a uma lista, pode usar o operador in.

gap> L1[3];
5
gap> 10 in L1;
true
gap> 10 in L2;
false
gap> "a" in L2;
true

A posição de um elemento em uma lista pode ser determinada usando a função Position.

gap> Position( L1, 10 );
6
gap> Position( L1, -1 );
fail

Frequentamente, precisa-se criar novas listas usando listas. Por exemplo, frequentamente queremos criar a lista de elementos de uma outra lista que satisfazem uma certa propriedade. Esta tarefa pode ser resolvida usando a função Filtered( list, func ) em GAP onde list é uma lista e func é uma função (Seção 5.6) que devolve true ou false (Seção 2.2). Nos seguintes exemplos veremos alguns usos simples desta construção.

# os números pares em L1
gap> Filtered( L1, IsEvenInt );
[ 10, 8, 6, 4, 2, 0 ]
# os números ímpares em L1
gap> Filtered( L1, IsOddInt );
[ 1, 3, 5, 7, 9 ]
gap> Filtered( L1, x -> x mod 2 = 0 );
[ 10, 8, 6, 4, 2, 0 ]
gap> Filtered( L1, x -> x mod 2 = 1 );
[ 1, 3, 5, 7, 9 ]

Novas listas podem ser criadas também aplicando uma função nos elementos de uma outra lista. Por exemplo, criamos a lista dos quadrados dos primeiros 10 números naturais:

gap> List( [1..10], x->x^2 );
[ 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 ]

GAP trabalha também com listas nas quais algumas entradas não estão definidas. Tais listas são chamadas de listas esparsas. Considere por exemplo as seguintes instruções.

gap> l := [1,2,,,12];
[ 1, 2,,, 12 ]
gap> l[1];
1
gap> l[2];
2
gap> l[3];
Error, List Element: <list>[3] must have an assigned value
not in any function at *stdin*:166
type 'quit;' to quit to outer loop
brk> quit;
gap> IsBound( l[3] );
false
gap> IsBound( l[4] );
false
gap> IsBound( l[5] );
true
gap> l[5];
12
gap> 
gap> l[8] := 22;
22
gap> l;
[ 1, 2,,, 12,,, 22 ]

Note que, ao acessar l[3], obtemos um erro, pois esta entrada não existe. Para evitar este erro, podemos verificar se existe ou não a entrada usando IsBound.

3.2 Tarefa

Construa as seguintes listas em GAP.

1. A lista dos naturais entre \(1\) e \(50\).
2. A lista dos naturais pares entre \(1\) e \(50\).
3. A lista dos naturais ímpares entre \(1\) e \(50\).
4. Os primos entre \(1\) e \(50\). (Use a função IsPrimeInt).
5. A lista dos naturais entre \(1\) e \(50\) que dão resto \(3\) módulo \(5\) (veja Seção 2.1).

3.3 Matrizes

Em GAP, uma matriz é lista de listas (que são as linhas da matriz) (manual). As entradas de matrizes são tipicamente números ou, mais geralmente, elementos de um anel ou corpo. As matrizes podem ser somadas e multiplicadas exatamente como números.

gap> m1 := [[1,2,0],[0,-2,3]];
[ [ 1, 2, 0 ], [ 0, -2, 3 ] ]
gap> Display( m1 );
[ [   1,   2,   0 ],
  [   0,  -2,   3 ] ]
gap> m2 := [[1,-1],[0,3],[4,1/2]];
[ [ 1, -1 ], [ 0, 3 ], [ 4, 1/2 ] ]
gap> Display( m2 );
[ [    1,   -1 ],
  [    0,    3 ],
  [    4,  1/2 ] ]
gap> m1*m2;
[ [ 1, 5 ], [ 12, -9/2 ] ]
gap> Display( last );
[ [     1,     5 ],
  [    12,  -9/2 ] ]
gap> m2*m1;
[ [ 1, 4, -3 ], [ 0, -6, 9 ], [ 4, 7, 3/2 ] ]
gap> Display( last );
[ [    1,    4,   -3 ],
  [    0,   -6,    9 ],
  [    4,    7,  3/2 ] ]

Para acessar uma entrada em uma matriz, pode usar m[i][j]. Por exemplo

gap> m1[2,1];
0

Determinantes e matrizes inversas podem ser calculados por Determinant( m ) e m^-1.

gap> m := [[1,2,0],[0,-2,3],[0,1,0]];
[ [ 1, 2, 0 ], [ 0, -2, 3 ], [ 0, 1, 0 ] ]
gap> Determinant( m );
-3
gap> mi := Inverse( m );
[ [ 1, 0, -2 ], [ 0, 0, 1 ], [ 0, 1/3, 2/3 ] ]
gap> m*mi;
[ [ 1, 0, 0 ], [ 0, 1, 0 ], [ 0, 0, 1 ] ]

3.4 Tarefa

1. Defina as seguintes matrizem em GAP. \[ M_1 := \begin{pmatrix} 0 & 1 & -2 \\ 1 & 0 & 1 \\ -1 & 1 & 2\end{pmatrix} \] e \[ M_2 := \begin{pmatrix} -1 & 1 & 2 \\ 2 & -1 & 0 \\ 3 & 0 & -1\end{pmatrix}. \]
2. Calcule os determinantes de \(M_1\) e \(M_2\) e as inversas, caso forem invertíveis.
3. Calcule o comutador \(M_1M_2-M_2M_1\) na álgebra de matrizes e o comutador \(M_1^{-1}M_2^{-1}M_1M_2\) no grupo.
4. Considere as mesmas matrizes \(M_1\) e \(M_2\) mas agora com entradas no corpo \(\mathbb F_5\) (Seção 2.4) e repita as computações nos itens anteriores.
   

Para obter as matrizes no item 4., pode multiplicar as matrizes já definidas no item 1. com One( GF( 5 )) ou com Z( 5 )^0.

3.5 Permutações

Outro objeto fundamental quando trabalhamos com grupos finitos é a permutação. Permutações em GAP podem ser definidas como produto de cíclos disjuntos mas também usando uma lista.

gap> p1 := (1,2,3)(4,5,6);
(1,2,3)(4,5,6)
gap> p1^2;
(1,3,2)(4,6,5)
gap> p2 := PermList( [1,5,4,3,2] );
(2,5)(3,4)
gap> p1*p2;
(1,5,6,3)(2,4)
gap> p2*p1;
(1,2,6,4)(3,5)

3.6 Tarefa

1. Construa a lista de todas as permutações em três pontos.
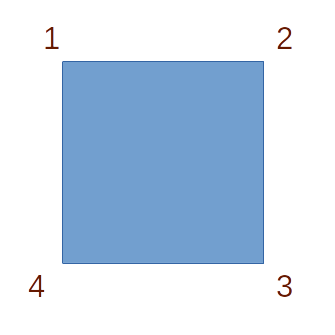
2. Construa a lista das 8 permutações que representam as simetrias de um quadrado com pontas \(1\), \(2\), \(3\), e \(4\) (nesta ordem).

No item 2., considere as quatro rotações e as quatro reflexões do seguinte quadrado.

quadrado