15 Polynômios, ideais, e um problema de triângulos

Neste projeto, aprendemos como trabalhar com polinômios, anéis polinomiais, ideais em GAP e resolvemos um problema de geometria plana.

15.1 Polynômios em GAP

Indeterminados, polinômios e anéis de polinômios podem ser definidos em GAP na maneira seguinte.

gap> x := Indeterminate( Rationals, "x" );
x
gap> y := Indeterminate( Rationals, "y" );
y
gap> z := Indeterminate( Rationals, "z" );
z
gap> P := PolynomialRing( Rationals, [x,y,z] );
Rationals[x,y,z]
gap> f := x*y-z^2;
x*y-z^2
gap> g := x^2+z^2;
x^2+z^2
gap> f*g;
x^3*y-x^2*z^2+x*y*z^2-z^4

Note que podemos também definir ideais.

gap> I := Ideal( P, [f,g] );
<two-sided ideal in Rationals[x,y,z], (2 generators)>

Considere \[ h=x^2yz-xz^3-x^3-xz^2+xy-z^2. \] Verifiquemos se \(h\) pertence ao ideal \(I=(f,g)\).

gap> h := h=x^2*y*z-x*z^3-x^3-x*z^2+x*y-z^2;
gap> I := Ideal( P, [f,g] );
<two-sided ideal in Rationals[x,y,z], (2 generators)>
gap> h in I;
true

Portanto \(h\) pode ser escrito na forma \[ h=uf+vg\quad\mbox{com}\quad u,v\in\mathbb Q[x,y,z]. \] Vamos ver como achar os polinômios \(u\) e \(v\).

gap> PolynomialReduction( h, [f,g], MonomialLexOrdering() );
[ 0, [ x*z+1, -x ] ]

O resultado indica que o resto de \(h\) em relação ao ideal \(I\) é \(0\) e os dois polinômios do segundo componente do output podem ser tomados para \(u\) e \(v\).

gap> h = (x*z+1)*f-x*g
true

15.2 As medianas de um triângulo

Seja \(\Delta=ABC\) um triângulo no plano. A reta que conecta uma ponta de \(\Delta\) com o ponto meio do lado oposto chama-se mediana. Está bem conhecido que as medianas se interceptam em um ponto chamado de baricentro de \(\Delta\). Neste projeto provaremos este fato usando álgebra comutativa.

Assuma sem perder generalidade que as três pontas do triângulo são \[\begin{align*} A & = (0,0);\\ B & = (1,0);\\ C & = (x,y). \end{align*}\] Assuma que \(P\), \(Q\) e \(R\) são os pontos médios dos lados \(BC\), \(AC\) e \(AB\). Portanto, \[\begin{align*} P & = ((x+1)/2,y/2);\\ Q & = (x/2,y/2);\\ R & = (1/2,0). \end{align*}\]

Os pontos estão ilustrados na seguinte imagem.

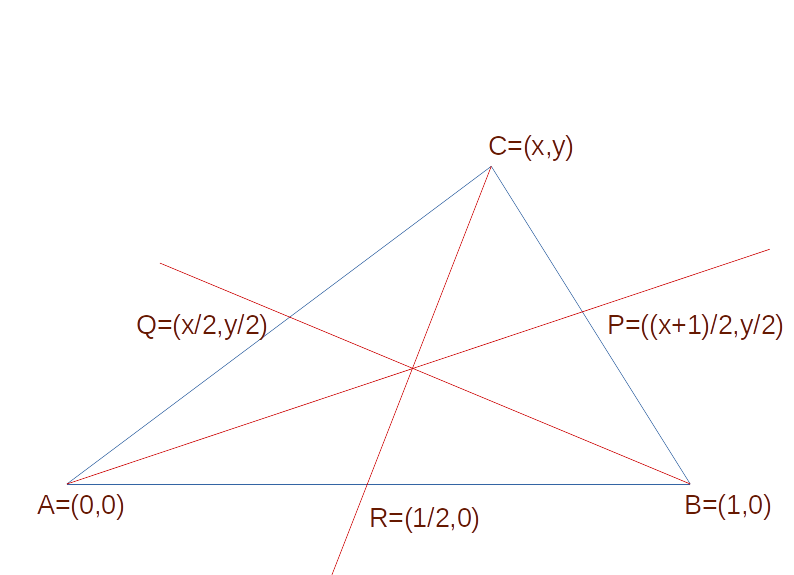
Assuma que \(S=(u,v)\) é o ponto de interseção das retas \(AP\) e \(BQ\). Precisa provar que a reta \(CR\) passa pelo ponto \(S\). Os fatos que \(S\) está na reta \(AP\) e que \(S\) está na reta \(BQ\) podem ser expressas das equações \[\begin{align*} \frac uv=\frac{x+1}y;\\ \frac{x-2}y=\frac{u-1}v. \end{align*}\] Como o triângulo não é degenerado, temos que \(u\neq 0\), \(v\neq 0\) e \(y\neq 0\) e estas equações são equivalentes com as equações \[\begin{align*} f_1&=uy-v(x+1)=0;\\ f_2&=(x-2)u-(u-1)y=0. \end{align*}\] Similarmente, o fato que \(S\) está na reta \(CR\) pode ser expressa pela equação \[ \frac{u-1/2}v=\frac{x-1/2}y; \] ou seja, \[ f_3=-2xv+2yu-y+v=0. \]

Para provar que \(S\) está na reta \(CR\), é suficiente provar que \(f_3=0\) sempre que \(f_1=0\) e \(f_2=0\). Isso segue do fato que \(f_3\) pertence ao ideal gerado por \(f_1\) e \(f_2\); ou seja, \[ f_3\in(f_1,f_2). \]

15.3 Tarefa 1

Faça as seguintes computações com GAP.

Defina o anel de polinômios \(\mathbb Q[x,y,u,v]\).
Defina os polinômios \(f_1,f_2,f_3\) em cima.
Verifique se \(f_3\in(f_1,f_2)\).
Escreva \(f_3\) na forma \[ f_3=h_1f_1+h_2f_2 \] onde \(h_i\in\mathbb Q[x,y,u,v]\).

Siga os passos na computação em cima.

15.4 Tarefa 2

O modelo algébrico não incluiu a informação que o triângulo é não degenerado; ou seja, \(y\neq 0\). Esta condição pode ser incluída no modelo por introduzir uma nova variável \(Y\) e uma nova equação \[ f_4=Yy-1=0. \]

Faça as computações na Tarefa 1 incluindo o polinômio \(f_4\). Verifique se o resultado é diferente.

15.5 Tarefa 3

Demonstre que o ponto \(S\) divide as medianas em duas partes cuja razão é \(1:2\). Note que esta afirmação é equivalente à equação \[ 3|RS|=3(u-1/2,v)=(x-1/2,y)=|RC|. \] Ou seja, precisa verificar que \[ 3u-x-1,\ 3v-y\in (f_1,f_2). \]

Verifique se estes dois polinômios estão no ideal \((f_1,f_2)\).
Escreve-os na forma \[ h_1f_1+h_2f_2. \]