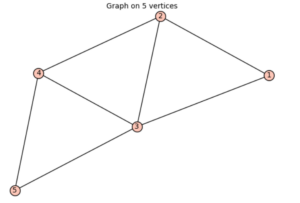
Queremos calcular quais são os vértices mais importantes desta rede. Sejam $p_1$, $p_2$, $p_3$, $p_4$, $p_5$ os pesos dos vértices considerando sua importância na rede. Na aula vimos que os números $p_i$ satisfazem o seguinte sistema de equações lineares.
\begin{align*}
\frac 13 p_2+\frac 14 p_3&= p_1\\
\frac 12 p_1+\frac 14 p_3+\frac 13 p_4&= p_2\\
\frac 12 p_1+\frac 13 p_2+\frac 13 p_4+\frac 12 p_5&= p_3\\
\frac 13 p_2+\frac 14 p_3+\frac 12 p_5&= p_4\\
\frac 14 p_3+\frac 13p_4&= p_5
\end{align*}
Usando, Scilab, a solução do sistema vai ser feita na maneira seguinte.
// definimos primeiro a matriz do sistema
A =
0. 0.3333333 0.25 0. 0.
0.5 0. 0.25 0.3333333 0.
0.5 0.3333333 0. 0.3333333 0.5
0. 0.3333333 0.25 0. 0.5
0. 0. 0.25 0.3333333 0.
// definimos uma matriz A1 como A menos a a matriz identidade
--> A1 = A - A^0
A1 =
-1. 0.3333333 0.25 0. 0.
0.5 -1. 0.25 0.3333333 0.
0.5 0.3333333 -1. 0.3333333 0.5
0. 0.3333333 0.25 -1. 0.5
0. 0. 0.25 0.3333333 -1.
// para obter as soluções, usamos a função linsolve
--> [x0,X] = linsolve( A1, [0;0;0;0;0] )
x0 =
0.
0.
0.
0.
0.
X =
0.3086067
0.4629100
0.6172134
0.4629100
0.3086067
Obtemos assim que
\begin{align*}
p_1&=0.3086067\\
p_2 &= 0.3086067\\
p_3 &= 0.6172134\\
p_4 &= 0.4629100\\
p_5 &= 0.3086067
\end{align*}
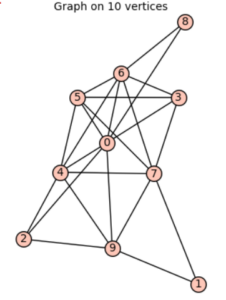
Calcule os pesos dos vértices $0,1,\ldots,9$ deste grafo em termos da sua importância seguindo os passos no exemplo anterior.