O problema da interpolação

Sejam $P_1=(1,1)$, $P_2=(-1,1)$, $P_3=(2,1)$ e $P_3=(-2,-11)$ quatro pontos no plano. Queremos achar uma função polinomial
\[
f(x)=\alpha_3 x^3+\alpha_2 x^2+\alpha_1 x+\alpha_0
\]
tal que o grafo de $f(x)$ passe pelos pontos $P_1$, $P_2$, $P_3$, $P_4$. Em outras palavras,
\[
f(1)=1,\quad f(-1)=1,\quad f(2)=1,\quad f(-2)=-11.
\]
Substituindo em $f(x)$ obtemos o seguinte sistema de equações lineares.
\begin{align*}
\alpha_0+\alpha_1+\alpha_2+\alpha_3&=1\\
\alpha_0-\alpha_1+\alpha_2-\alpha_3&=1\\
\alpha_0+2\alpha_1+4\alpha_2+8\alpha_3&=1\\
\alpha_0-2\alpha_1+4\alpha_2-8\alpha_3&=-11
\end{align*}
Para resolver o problema da interpolação, precisamos resolver o sistema acima.

// definimos a matriz do sistema
A = [ 1 1 1 1; 1 -1 1 -1; 1 2 4 8; 1 -2 4 -8 ]
 A  = 

   1.   1.   1.   1.
   1.  -1.   1.  -1.
   1.   2.   4.   8.
   1.  -2.   4.  -8.

// definimos o vetor b
--> b = [1;1;1;-11] 
 b  = 

   1.
   1.
   1.
  -11.

// calculamos a solução do sistema usando 
// o método da matriz inversa
--> A^-1*b
 ans  =

   3.0000000000000004440892
  -0.999999999999999888978
  -2.
   1.
 

Obtemos da computação que $\alpha_0=3$, $\alpha_1=-1$, $\alpha_2=-2$, $\alpha_3=1$. Ou seja, o polinômio procurado é
\[
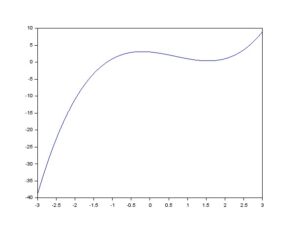
f(x)=x^3-2x^2-x+3
\]
Para visualizar o polinômio obtido, podemos executar as seguintes linhas.

// definimos primeiro o polinômio
--> p = poly( [3,-1,-2,1], "x", "coeff" )
 p  = 

  3 -x -2x^2 +x^3

// usamos a seguinte instrução para visualizar a curva
// a expressão "-3:0.1:3" significa a lista de valores 
// entre -3 e 3 com incremento de 0.1.
// 
// Esta linha deve abrir uma nova janela 
--> plot( -3:0.1:3, p )

Obtemos uma imagem da seguinte forma.